🏆🏆🏆🏆🏆🏆🏆
欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
　
文章字体风格：
红色文字表示：重难点✔★
蓝色文字表示：思路以及想法✔★
　
如果大家觉得有帮助的话，感谢大家帮忙
点赞！收藏！转发！
　
我的qq号是：1210931886，欢迎大家加群，一起学习，互相交流，共同进步🎉🎉✨✨
🥇🥇🥇🥇🥇🥇🥇

蓝桥杯系列，为大家提供

1. 做题全集，备战蓝桥杯，就做这个系列的题即可
2. 一个大概的做题规划——大家最好在此基础上提前两个月准备

备战蓝桥杯就刷这些题
第一天博客链接 - 基础算法 -上
第二天博客链接 - 基础算法 -下 + 数据结构专题
第三天博客链接 - 搜索与图论-上 专题
第四天博客链接 - 搜索与图论-下 专题
第五天博客链接 - 数学知识专题
第六天博客链接 - 动态规划 专题
第七天博客链接 - 贪心算法 专题

9. spfa 算法

1. spfa求最短路 ✔12.24

原题链接

做题总结：

1. 和宽搜差不多，只是可能会 返回走（但距离值更新了，就把这个节点入队列再处理一次）

#include<iostream>
#include<cstring>
#include<queue>

using namespace std;

const int N = 1e5+10;
int e[N],ne[N],h[N],idx;
int w[N];

bool st[N];

int n,m;

void add(int x,int y,int c)
{
    e[idx] = y,ne[idx] = h[x],w[idx] = c,h[x] = idx++;
}

int d[N];

void spfa()
{
    memset(d,0x3f,sizeof d);
    d[1] = 0;
    queue<int> q;
    q.push(1);
    st[1] = true;
    while(q.size())
    {
        auto f = q.front();
        q.pop();
        st[f] = false;
        for(int i = h[f]; i != -1; i = ne[i])
        {
            int j = i;
            if(d[e[j]] > d[f] + w[j])
            {
                d[e[j]] = d[f] + w[j];
            if(st[e[j]]==false)
            {
                q.push(e[j]);
                st[e[j]] = true;
            }
                
            }
        }
    }
}

int main()
{
    cin >> n >> m;
    memset(h,-1,sizeof h);
    for(int i = 0; i < m; i++)
    {
        int x,y,c;
        cin >> x >> y >> c;
        add(x,y,c);
    }
    
    spfa();
    if(d[n] == 0x3f3f3f3f)
        cout << "impossible";
    else
        cout << d[n];
    return 0;
}

10. spfa判断负权回路

原题链接

1. 什么是负环
   
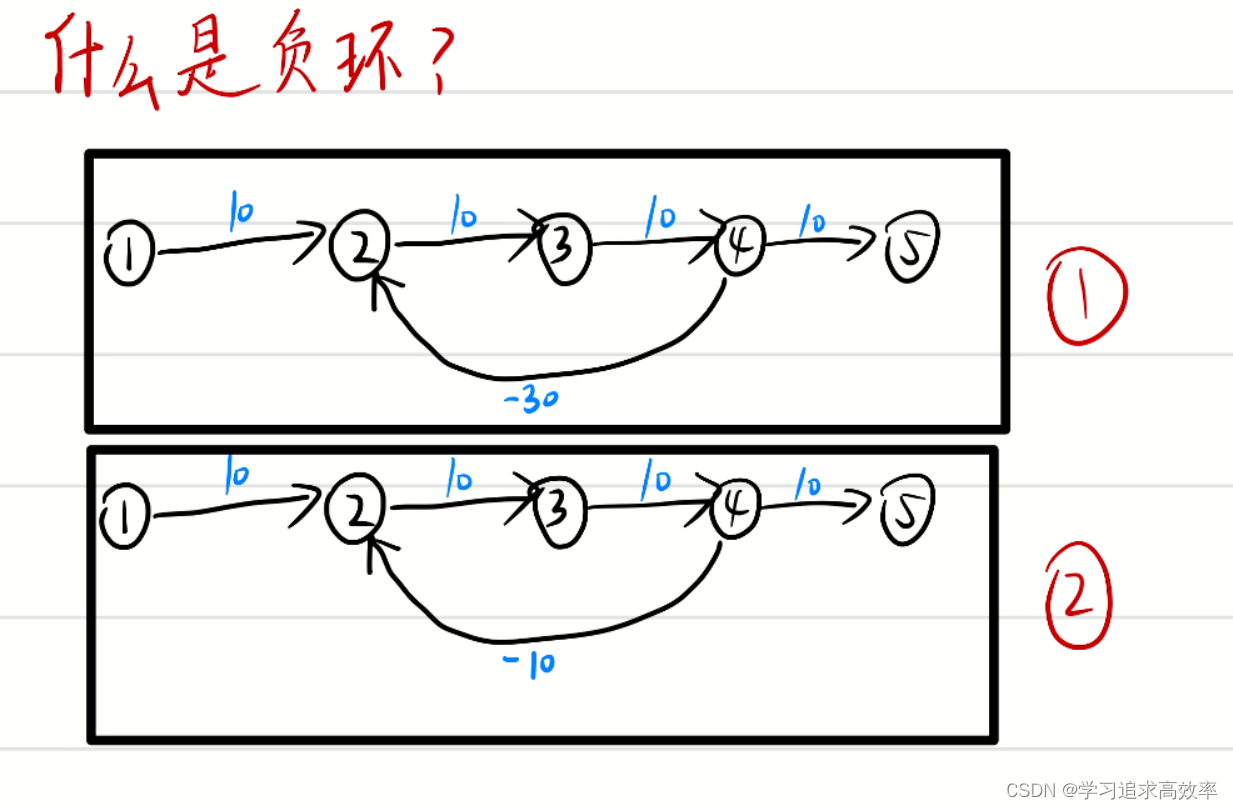
   图1中：2 到 3 到 4 到 2 路径长度为 -10
   图2中：2 到 3 到 4 到 2 路径长度为 10

图1才叫负环
图2不是负环

2. 出现负环会怎么样
   但出现负环的时候，如果我们要去求1到n的最短路，那么过程中，一定会在这个负环中一直转圈，导致路程可以变为负无穷

3. 怎么判断图中是否有负环？
   综上，我们就采取求最小路径的方式（但是本题不是求最短路），当我们求最短路径的过程中，发现有一段路径重复走，那么就说明一定出现了负环

问题来了：怎么判断某段路径在重复走
我们想，1到n号点 最多才可能走了n-1条边
如果我们发现 到某点时 已经走了 大于等于n条边，那么一定就是有负环了
由于我们不知道 1 到 x点最多可能有多少条边，但一定不会超过 n - 1 条边，所以我们就都用 大于等于n条边去判断

例题 spfa判断负环 ✔12.26

原题链接

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 2010, M = 10010;

int n, m;
int h[N], w[M], e[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

bool spfa()
{
    queue<int> q;

    for (int i = 1; i <= n; i ++ )
    {
        st[i] = true;
        q.push(i);
    }

    while (q.size())
    {
        int t = q.front();
        q.pop();

        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;

                if (cnt[j] >= n) return true;
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return false;
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    if (spfa()) puts("Yes");
    else puts("No");

    return 0;
}

刷题总结

1. e,ne,h,idx 用于存储边，所以数值应该与边一样多
2. 把所有点都入队列，防止不是连通图
3. dist里存储多少都可以，因为我们只需判断负权回路
4. 当一个点所走的路径长度大于n，那么就一定有负边，因为最多就是n正常的话。
5. 一定要有st数组，判断是否再走这个点

11. floyd算法( 两两之间最短距离 )

1. Floyd求最短路 ✔12.26

原题链接

做题总结

1. 用二维数组存储更方便
2. 读入存储的时候，读取最小值，并且到自身值为0
3. Floyd

#include<iostream>
#include<cstring>

using namespace std;
int n,m,k;
const int N = 210;
int d[N][N];

void Floyd()
{
    for(int k = 1; k <= n; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j],d[i][k]+d[k][j]);
}

int main()
{
    cin >> n >> m >> k;
    memset(d,0x3f,sizeof d);
    for(int i = 0; i < m; i++)
    {
        int x,y,c;
        cin >> x >> y >> c;
        d[x][y] = min(d[x][y], c);
        d[x][x] = 0;
        d[y][y] = 0;
    }
    Floyd();
    for(int i = 0; i < k; i++)
    {
        int x,y;
        cin >> x >> y;
        if(d[x][y]>=0x3f3f3f3f/2)
            cout << "impossible" << endl;
        else
            cout << d[x][y] << endl;
    }
    
    return 0;
}

12. 朴素版prim算法

1. Prim算法求最小生成树

原题链接

做题总结

1. 和dijk算法差不多 只是 dist数组存储的是 到联通块的距离

#include<iostream>
#include<cstring>

using namespace std;

const int N = 510;
int p[N][N], d[N];
int n, m;
bool st[N];
int res;
int sum;

void prim()
{
    memset(d, 0x3f, sizeof d);
    d[1] = 0;

    for (int k = 0; k < n; k++)
    {
        int t = -1;

        for (int l = 1; l <= n; l++)
        {
            if (st[l] == false && (t == -1 || d[t] > d[l]))
                t = l;
        }
        if (d[t] == 0x3f3f3f3f)
        {
            res++;
            return;
        }
        st[t] = true;
        sum += d[t];
        for (int i = 1; i <= n; i++)
        {
            d[i] = min(d[i], p[t][i]);
        }
    }
}

int main()
{
    memset(p,0x3f,sizeof p);
    cin >> n >> m;
    for (int i = 0; i < m; i++)
    {
        int x, y, c;
        cin >> x >> y >> c;
        p[x][y]= p[y][x] = min(p[x][y],c);
    }
    prim();
    if (res)
        cout << "impossible";
    else
        cout << sum;
    return 0;
}

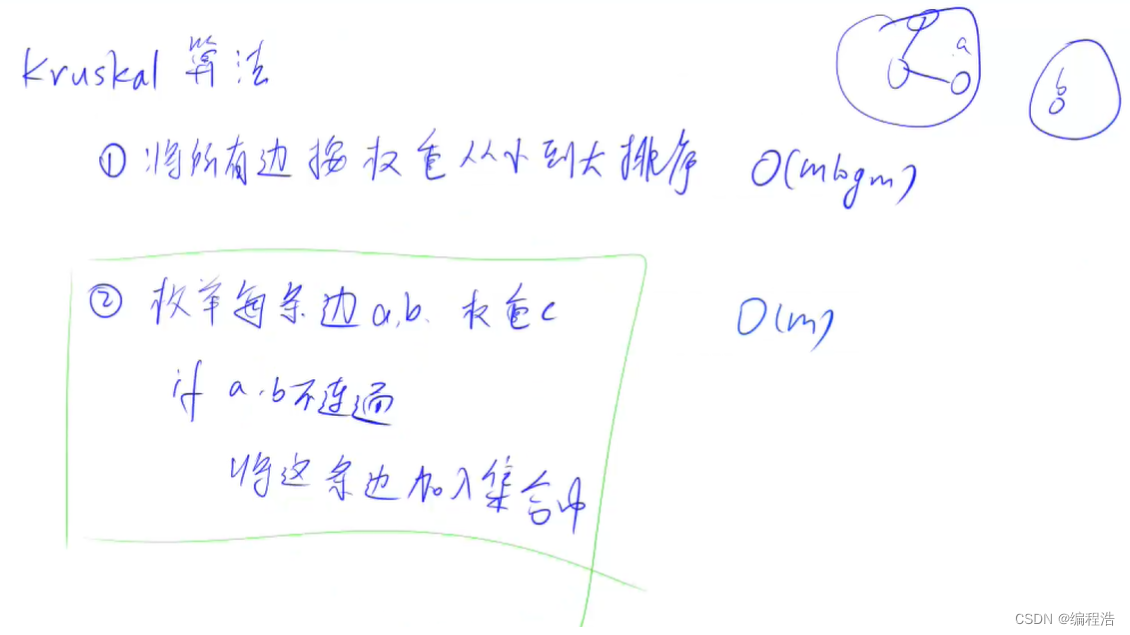
13. Kruskal算法

1. Kruskal算法求最小生成树( 利用并查集 )

原题链接
原题链接

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010, M = 200010, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge
{
    int a, b, w;

    bool operator< (const Edge &W)const
    {
        return w < W.w;
    }
}edges[M];

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;    // 初始化并查集

    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if (a != b)
        {
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }

    if (cnt < n - 1) return INF;
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);

    for (int i = 0; i < m; i ++ )
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }

    int t = kruskal();

    if (t == INF) puts("impossible");
    else printf("%d\n", t);

    return 0;
}

14. 染色法判别二分图

染色法判定二分图 ✔ 12.28

算法思路 + 做题总结

算法思路

1. 通过dfs 一个染1 另一个染2（通过3-c）
2. dfs需要有返回值。所以当 下一个返回来的是false，那么就返回false
   所以一个dfs中，通过判断有一个return false，并且还有一个根据下一个的return 再return false

做题总结

1. 无向图 需要开辟 2倍

原题链接

原题链接

#include<iostream>
#include<cstring>

using namespace std;

const int N = 2e5+10;

int e[N],ne[N],h[N],idx;
int color[N];
bool st[N];
int n,m;

void add(int a,int b)
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}

bool dfs(int x,int c)
{
    st[x] = true;
    color[x] = c;
    for(int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(st[j]==true)
        {
            if(color[j]==color[x])
                return false;
        }
        if(st[j] == false)
        {
            if(!dfs(j,3-c))
                return false;
        }
    }
    return true;
}

int main()
{
    cin >> n >> m;
    memset(h,-1,sizeof h);
    
    for(int i = 0; i < m; i++)
    {
        int x,y;
        cin >> x >> y;
        add(x,y),add(y,x);
    }
    
    bool flag = false;
    for(int i = 1; i <= n; i++)
    {
        if(st[i]==false)
        {
            if(!dfs(i,1))
            {
                flag = true;
                break;
            }
        }
    }
    
    if(flag == true)
        cout << "No";
    else
        cout << "Yes";
    
    return 0;
}

15. 匈牙利算法

模板

时间复杂度是 O(nm)O(nm), nn 表示点数，mm 表示边数

int n1, n2;     // n1表示第一个集合中的点数，n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx;     // 邻接表存储所有边，匈牙利算法中只会用到从第一个集合指向第二个集合的边，所以这里只用存一个方向的边
int match[N];       // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N];     // 表示第二个集合中的每个点是否已经被遍历过

bool find(int x)
{
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true;
            if (match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }

    return false;
}

// 求最大匹配数，依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
    memset(st, false, sizeof st);
    if (find(i)) res ++ ;
}

二分图的最大匹配 ✔12.29

原题链接

做题总结：

1. 避免多次重复问一个女生，所以遍历每次男生时，用st存储该男生是否考虑过这个女生，这样其他男生就别再考虑了