1、斐波那契数列

本题考点： 间复杂度，fib理解，剪枝重复计算 牛客链接

题目描述：

解题思路：

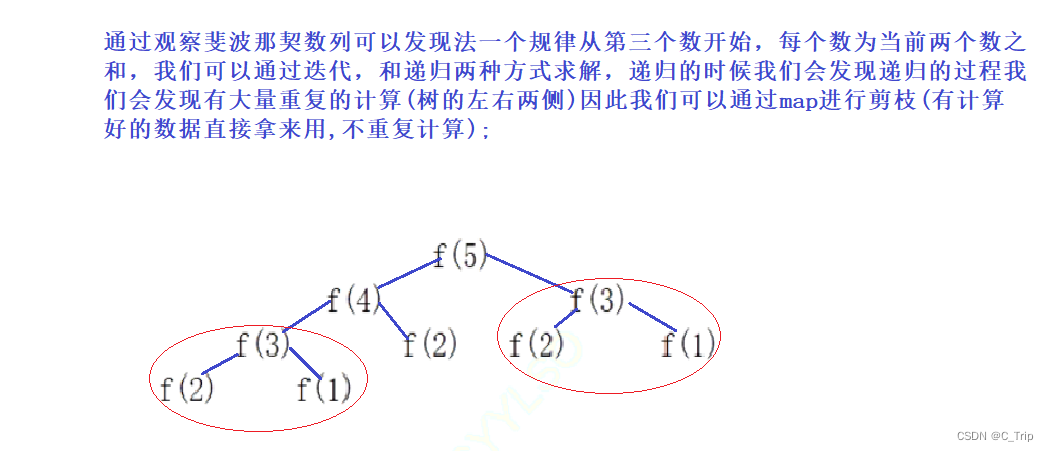
代码：

class Solution {
public:

    //迭代
    // int Fibonacci(int n) {
    //     int ret = 0;
    //     int a = 1, b = 1;
    //     if(n <= 2)
    //         return 1;
    //     for(int i = 3; i <= n; i++)
    //     {
    //         ret =a + b;
    //         a = b;
    //         b = ret;
    //     }
    //     return ret;
    // }

    //递归，剪枝
    int Fibonacci(int n) {
        if(n == 0)
            return 0;
        if(n <= 2)
            return 1;
        
        int pre = 0, ppre = 0;
        if(mp.find(n - 2) == mp.end())
        {
            //没找到,递归求解
            ppre = Fibonacci(n - 2);
            mp.insert({n - 2, ppre});
        }
        else
        {
            //找到了
            ppre = mp[n - 2];
        }

        if(mp.find(n - 1) == mp.end())
        {
            //没找到
            pre = Fibonacci(n - 1);
            mp.insert({n - 1, pre});
        }
        else
        {
            //找到了,递归求解
            pre = mp[n - 1];
        }
        
        return pre + ppre;
    }

private:
    map<int, int> mp;
};

2、跳台阶

本题考点： 场景转化模型，模型提取解法，简单dp 牛客链接

题目描述：
一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。
数据范围：1≤n≤40
要求：时间复杂度：O(n) ，空间复杂度： O(1)

解题思路：

代码：
本题代码和上一题一样，参照上一题代码即可。

3、矩形覆盖

本题考点： 和上题相同 牛客链接

题目描述：
我们可以用 2 * 1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2 * 1 的小矩形无重叠地覆盖一个 2 * n 的大矩形，从同一个方向看总共有多少种不同的方法？

数据范围：0≤n≤38
进阶：空间复杂度O(1) ，时间复杂度 O(n)
注意：约定 n == 0 时，输出 0
比如n=3时，2*3的矩形块有3种不同的覆盖方法(从同一个方向看)：

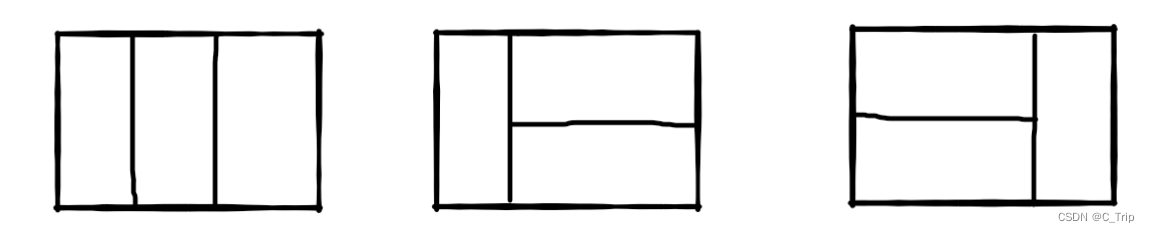
解题思路：

代码：

class Solution {
public:
    int rectCover(int number) {
        if(number < 2)
            return number;
        int* dp = new int[number + 1];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3; i<= number; i++)
        {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[number];
    }
};

4、二进制中1的个数

本题考点： 二进制计算 牛客链接

题目描述：
输入一个整数 n ，输出该数32位二进制表示中1的个数。其中负数用补码表示。
数据范围：-2^31 <= n <= 2 ^31 - 1
即范围为:−2147483648<=n<=2147483647

解题思路：

代码：

class Solution {
public:
    int  NumberOf1(int n) {

        //方法一：
   
        // int count = 0;
        // for(int i = 0; i < 32; i++)
        // {
        //     if(((n >> i) & 1 ) == 1)
        //         count++;
        // }
        // return count;
        
        //方法二：
        int count = 0;
        while(n)
        {
            n &= (n - 1);
            count ++;
        }
        return count;
    }
};

5、判断是否是素数

题目描述： 牛客链接
质数(又称素数),是指在大于1的自然数中,除了1和它本身外,不能被其他自然数整除(除0以外)的数称之为素数(质数)。请写个程序判断输入的数字是否是质数，如果是素数请输出：true，不是请输出false
请注意算法效率，该题目有时间限制 , 输入的数字小于2^64 次幂

解题思路：

代码：

#include<iostream>
#include<cmath>
using namespace std;
/*
//这种方法在此题中不行，效率达不到
bool isPrime(long long n ) 
{
    for(long int i = 2; i <= sqrt(n);i++)
    {
        if(n % i == 0)
        {    
            return false;
        }
    }
    return true;
}*/

bool isPrime(long long& n) {
    return (n == 2 || n == 3) || (n % 6 == 1) || (n % 6 == 5) ? true : false;
}
int main()
{
    long long n = 0;
    while(cin >> n)
    {
        if(isPrime(n))
            cout << "true" << endl;
        else
            cout << "false" << endl;
    }
    return 0;
}