前面我们介绍了有关动态规划的相关内容，相信大家也都有了一些收获，下面我们学习的列车继续驶往“图与网络分析”的站点，在本次文章中我们将一起走近图论的奠基人——欧拉Leonhard Euler，希望能给大家学习运筹学的旅程中带来不一样的感悟。

一、图论的发展简史及应用

01图论的诞生：哥尼斯堡七桥问题

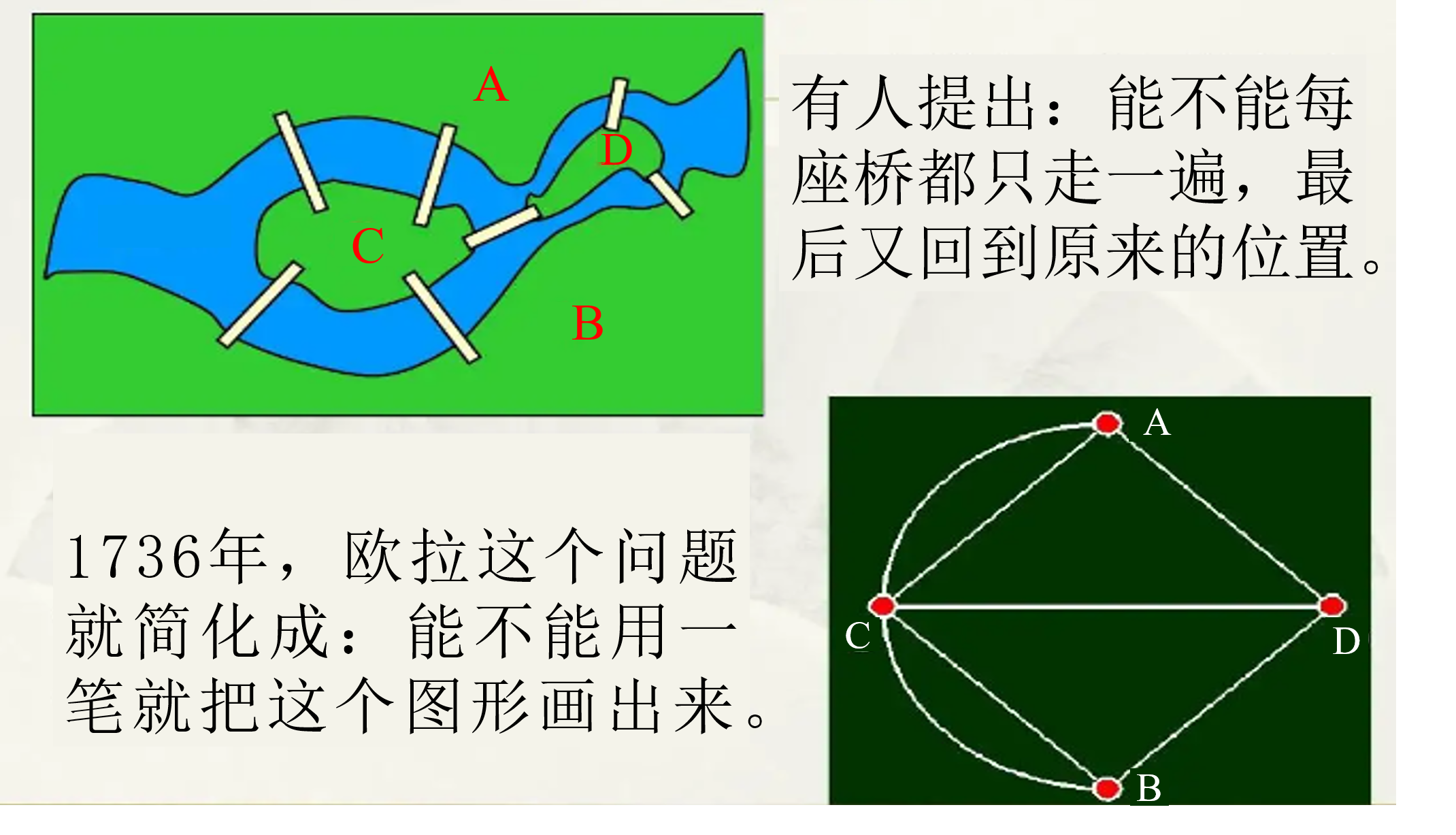
十八世纪，在今天俄罗斯加里宁格勒市还被称为哥尼斯堡的年代。像其他许多大城市一样，一条大河(普列戈利亚河)穿城而过。哥尼斯堡除了被一分为二以外，还包含河中的两个岛屿，人们建有七座桥梁连接着不同的陆地。

当时有一个著名的游戏谜题，就是在所有桥都只能走一遍的前提下，怎样才能把这片区域所有的桥都走遍？

这个谜题成为当地人一项热衷的消遣运动，许多人声称已经找到了这样一条路径，但当被要求按照规则再走一遍时，却发现还是没有人能够做到。

直到1736年，瑞士数学家欧拉给出了答案，他在论文《The seven bridges of Königsberg》中解释了其中的原因，证明这样的步行方式并不存在，并在文中提出和解决了一笔画问题。欧拉对这一问题的详细阐释标志着图论的诞生，同时也对拓扑学的思想起到了启蒙作用。

02图论的发展热潮：汉密尔顿回路

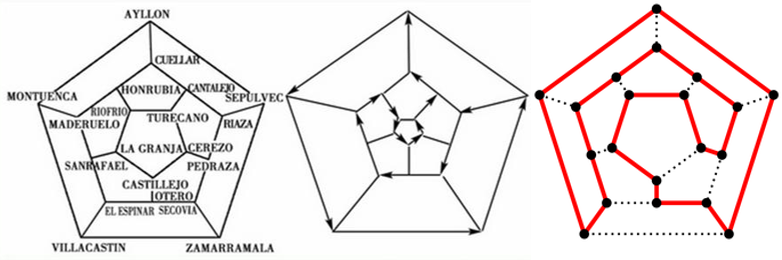
1857年英国数学家汉密尔顿William Rowan Hamilton发明了“周游世界”玩具，用一个正十二面体的20个顶点表示世界上20个大城市，30条棱代表这些城市之间的道路。要求游戏者从任意一个城市(即顶点)出发，延棱行走经过每个城市一次且只经过一次，最终返回出发地。汉密尔顿将此问题称为“周游世界”问题，并且作了肯定的回答。以下是一种走法。

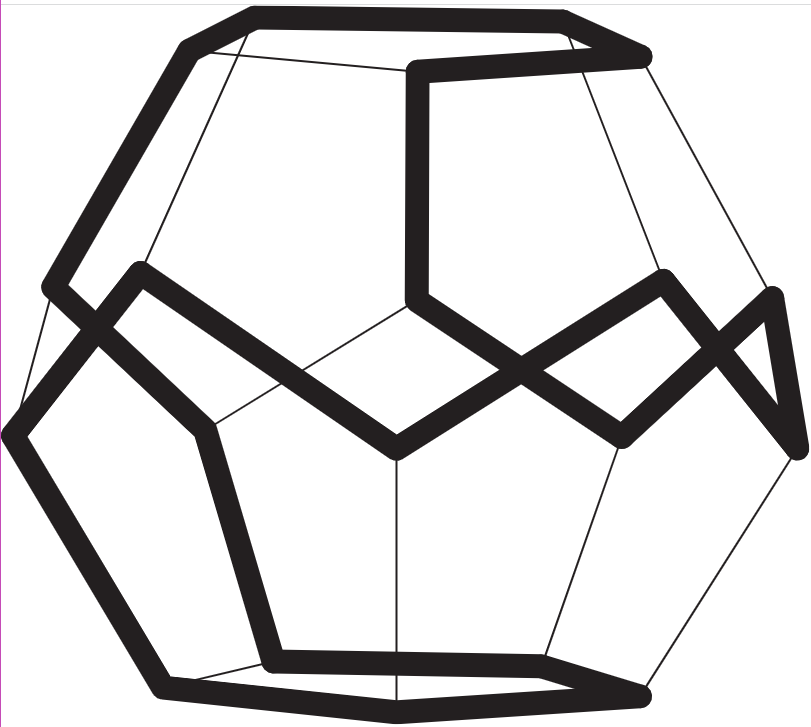
这个问题和哥尼斯堡七桥问题的不同之处在于，七桥问题是经过每条边一次，而汉密顿问题是经过每个顶点一次。汉密顿问题寻找一条从给定的起点到给定的终点沿途恰好经过所有其他城市一次的路径。

用图论的语言来说，游戏的目的是在十二面体的图中找出一个生成圈。这个生成圈后来被称为汉密尔顿回路，由此掀起了图论研究的热潮。

由于运筹学、计算机科学和编码理论中的很多问题都可以化为汉密尔顿问题，从而引起广泛的注意和研究。

03图论的推演：四色问题

四色问题是世界近代三大数学难题之一。最先是由一位叫格斯里（Francis Guthrie）的英国大学生提出来的。

1852年，毕业于伦敦大学的格斯里来到一家科研单位搞地图着色工作时，发现每幅地图都可以只用四种颜色着色。这个现象能不能从数学上加以严格证明呢？

1852年10月23日，格斯里的弟弟就这个问题的证明请教了他的老师、著名数学家德·摩尔根Augustus De Morgan，摩尔根也没能解决这个问题，于是写信向自己的好友、著名数学家汉密尔顿William Rowan Hamilton爵士请教，但直到1865年汉密尔顿逝世为止，问题也没有能够解决。

1872年，英国当时最著名的数学家凯利Cayley正式向伦敦数学学会提出了这个问题，于是四色猜想成了世界数学界关注的问题。

电子计算机问世以后，由于演算速度迅速提高，加之人机对话的出现，大大加快了对四色猜想证明的进程。就在1976年6月，美国数学家阿佩尔Kenneth Appel和德国数学家哈肯Wolfgang Haken在美国伊利诺斯大学的两台不同的电子计算机上，用了1200个小时，作了100亿个判断，结果没有一张地图是需要五色的，最终证明了四色定理，轰动了世界。到目前为止，四色定理还只能靠计算机验证证明。

四色问题作为最著名和最具启发性的图论问题，如今仍有许多数学家在努力地追求，试图从数学理论上证明。

一个多世纪以来，数学家们为证明这条定理绞尽脑汁，所引进的概念与方法刺激了拓扑学与图论的生长、发展。在“四色问题”的研究过程中，不少新的数学理论随之产生，也发展了很多数学计算技巧，极大得丰富了图论的内容。

04图论的应用

图论是运筹学的一个重要分支，它是建立和处理离散类数学模型的一个重要工具。用图论的方法往往能帮助人们解决一些用其它方法难于解决的问题。由于这种数学模型和方法直观形象，富有启发性和趣味性，深受人们的青睐。到目前为止，已被广泛地应用于系统工程、通讯工程、计算机科学及经济领域。传统的物理、化学、生命科学也越来越广泛地使用了图论模型方法。

二、图论的奠基人——欧拉

莱昂哈德·欧拉（Leonhard Euler，1707年4月15日～1783年9月18日），瑞士数学家、自然科学家。

生平纪事

欧拉1707年4月15日出生于瑞士的巴塞尔的牧师家庭，自幼受父亲的影响。13岁时入读巴塞尔大学，15岁大学毕业，16岁获得硕士学位。

1725年，欧拉来到圣彼得堡，开始了他的数学生涯。1733年，年仅26岁的欧拉担任了圣彼得堡科学院数学教授。过度的工作使他28岁得了眼病，右眼失明。1741年欧拉到柏林担任科学院物理数学所所长。1766年，重回圣彼得堡任职。

没过多久，左眼视力衰退，最后完全失明．不幸的事情接踵而来，1771年一场大火将他的书房和大量研究成果全部化为灰烬。沉重的打击，仍然没有使欧拉倒下．他以惊人的毅力，凭着记忆和心算进行研究，直到逝世。

欧拉回路与图论

哥尼斯堡七桥问题是18世纪著名古典数学问题之一。但在相当长的时间里，没有人能解出来。29岁的欧拉发表了《The seven bridges of Königsberg》的论文，圆满解决了这一问题，同时开创了数学新分支——图论。

欧拉把七桥问题的实质归于“一笔画”问题，即判断一个图是否能够遍历完所有的边而没有重复。很快他就判断出要一次不重复走遍哥尼斯堡的7座桥是不可能的。也就是说，多少年来，让无数人烧脑、试图发现的不重复的路线，根本就不存在。一个号称最烧脑且困扰无数人的难题，居然就是这样的最简单答案。

在论文中，欧拉将七桥问题抽象出来，得到欧拉回路关系：要使得一个图形可以一笔画，必须满足如下两个条件：1.图形必须是连通的。2.图中的“奇点”个数是0或2。（连到一点的数目如是奇数条，就称为奇点）

大道至简，欧拉天才地把一道著名古典数学难题简化成一道小学生习题，并写进了小学课本，叫做“七桥问题”。七桥问题播下了图论诞生与发展的种子。这门一开始以游戏形式出现，而且此后也一直没有完全失去这一特点的数学分支，在20世纪得到迅速发展，已经成为十分有用的重要数学分支。

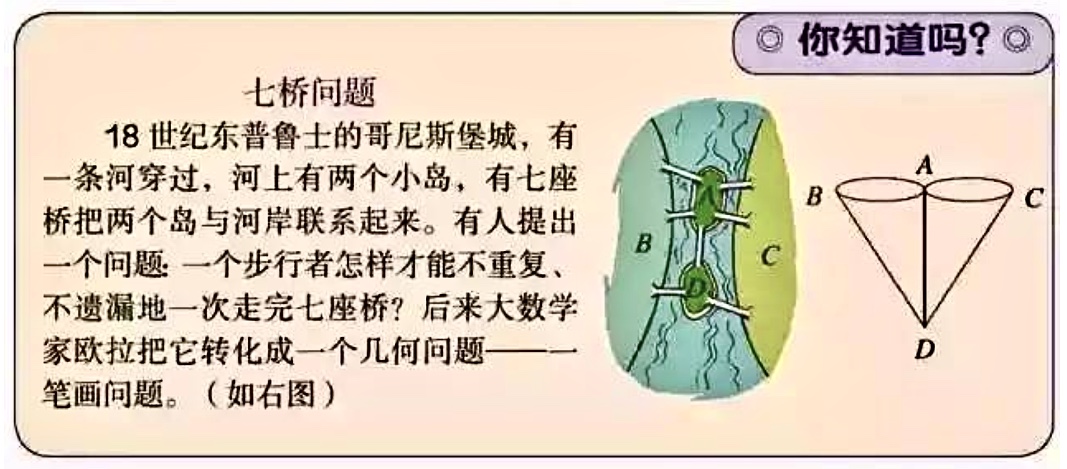
人教版六年级下册数学第104页

欧拉与中国

欧拉的著作最初传入中国，可追溯到大约250年前，由俄国传教士带进来，并送给天主教的一个支派“耶稣会”在中国的机构，曾收藏在北京天主教北堂的图书馆里。

然而，明、清年代中国数学已经日渐衰落，裹足不前，远远落后于欧洲。大约在乾隆年间传入中国的欧拉著作只能束之高阁，无人问津。

19世纪中叶，在李善兰与英国传教士合译的《代微积拾级》，华蘅芳与美国传教士傅兰雅合译的《微积溯源》中都介绍了欧拉和他的工作。中国人开始知道这位数学大家了，欧拉也登上了晚清人编写的《畴人传》。

清末民初，西方的先进数学被引进中国，大学里开设了“微积分”等课程，这才使得越来越多的中国人认识了欧拉，学习他的数学。

大师评价

“Euler calculated without effort, just as men breathe, as eagles sustain themselves in the air.”——Francois Arago

欧拉计算起来轻松自如，就像人们呼吸，鹰在空中飞翔。（法国物理学家、天文学家阿拉戈）

“The study of Euler’s works will remain the best school for the different fields of mathematics, and nothing else can replace it.”—— Carl Friedrich Gauss

研究欧拉的著作永远是了解数学的最好方法。（德国著名数学家、物理学家、天文学家、几何学家，大地测量学家卡尔·弗里德里希·高斯）

“Our students of mathematics would profit much more from a study of Euler's Introductio in Analysin Infinitorum, rather than of the available modern textbooks.”——André Weil

今天的学生从欧拉的《无穷分析引论》中所能获得的益处, 是现代任何一本教科书都不能比拟的。（法国数学家安德烈·韦伊）

“Read Euler, read Euler, he is the master of us all.”——Pierre Simon Laplace

读读欧拉吧，他是我们所有人的导师。（法国数学家皮埃尔-西蒙·拉普拉斯）