【配电网重构】负荷平衡的配电网重构【含Matlab源码 2180期】

news2024/9/25 3:26:38

⛄一、负荷平衡的配电网重构

1 引言
配电网网络重构是指在正常或非正常运行条件下通过改变开关的开关状态来改变网络的拓扑结构。配电网故障恢复供电是指配电网发生故障后,在故障已被定位和隔离的基础上,研究如何恢复对无故障停电区域供电的问题,本文简称为故障恢复。故障恢复重构程序的主要作用是帮助调度员对故障恢复供电过程进行决策,其目标是在允许的操作条件和电气约束下,通过网络重构将停电区域的负荷尽可能地转移到正常馈线上。

目前文献中大多数故障恢复重构算法是基于开关操作序列的启发式搜索算法[1~4],这些算法的主要优点是速度快。另有一些算法则采用了优化算法和启发算法相结合的算法,它可有效地实施供电恢复的开关操作[5]。这些算法的优点是可以不依赖于原始的系统结构,但当可行方案不存在时,它就无法提供一个能尽量减少难以避免的负荷失电的最佳方案。因此,它不适用于实时应用环境。为获得高效和鲁棒性能,本文采用了将启发式规则和模糊逻辑相结合的算法,它能为运行人员提供实时运行决策的支持工具。

本文提出的算法能实现以下功能:(1)对故障区的恢复供电。即隔离故障区域;给非故障停电区域供电;尽量减少不可避免的负荷失电。(2)为减轻配电系统过负荷而实施负荷平衡。

2.4 负荷平衡算法
2.4.1 负荷平衡算法归纳
1)根据文献[5]将层分配到各线路区段。

2)从位于离变电站最远的层中的线路段或配电设备开始,识别过负荷线路区段。

3)使用上述方法确定能减轻同一层中所有馈线区段上的过负荷的开关操作。

4)使用模糊逻辑方法选择能减轻每一层中的过负荷的最优方案。该方案使上层中的其它过负荷线路区段的过负荷最轻,同时能获得最少的开关操作次数。

2 模糊逻辑推理方法
在不同程度上具有某种特定性质的所有元素的总和称为模糊集合,其外延和内涵都是模糊的。用来描述一模糊集合中元素隶属该集合程度的特征函数称为隶属函数,用U来表示。隶属函数的值在0和1之间,其值越大表示该元素隶属于该集合的程度越深。

采用启发式算法,可找到许多能减轻一特殊层中线路区段过负荷的方案。而为了将负荷转移到上层中的线路区段,最终只需要采用其中的一种方案,摒弃其它方案。采用以下的模糊逻辑方法来选择最优方案:(1)开关操作次数;(2)被减轻的过负荷数目;(3)边界开关的容量裕度。3个隶属函数可用变量N、OL和CM来表示。

(1)开关操作次数N
由于目前我国配电网中手动开关占大多数,开关操作次数的多少影响着恢复供电的时间,因此开关操作次数是评估方案的重要指标。隶属函数U(N)如图1所示。图中,N为开关操作次数;Ns为可利用的边界开关总数;Nmin为操作员根据经验确定的最少开关操作次数。如可确定为1或3,即认为开关操作次数不超过Nmin时恢复方案很好,但随着开关操作次数的增加而使恢复方案逐渐变差。
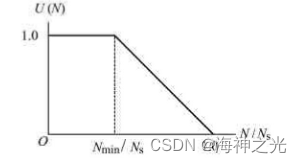
在这里插入图片描述
图1 隶属函数U(N)
(2)过负荷总数OL
其隶属函数U(OL)如图2所示。图中OL0为初始操作点的总过负荷量;OL为过负荷总量。

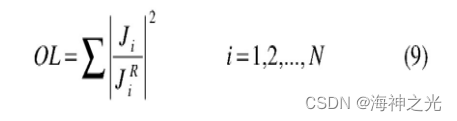
式中Ji为过负荷线路I的线路区段电流;JiR为线路的载流容量。

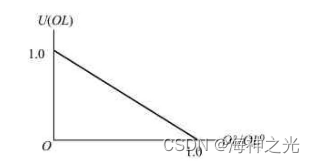
图2 隶属函数U(OL)
(3)边界开关总容量裕度CM
隶属函数U(CM)如图3所示。图中CM为边界开关总容量裕度;CM0为在初始运行条件下的边界开关总容量裕度。

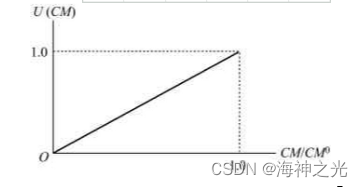
在这里插入图片描述
图3 隶属函数U(CM)
应用模糊逻辑方法选择最优的减轻过负荷方案的步骤(对每一过负荷的层,搜寻能减轻该层过负荷的所有方案)为:

(1)计算每一层的U(N)、U(OL)和U(CM);

(2)确定每一层的隶属函数值Us,该值即为U(N)、U(OL)和U(CM)的最小值。这样,方案I的隶属函数值为
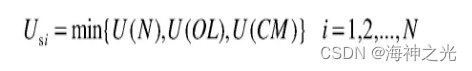
在这里插入图片描述
(3)选择该层中减轻过负荷的最优方案,即隶属函数值最大的方案:

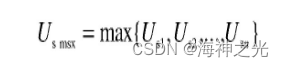
⛄二、部分源代码

clear
format long
dt=[2 2 -1 -1 1
0 1 3 -1 2
0 2 13 -1 3
0 13 5 -1 4
0 4 6 -1 5
0 5 7 -1 6
2 6 -1 -1 7
0 13 9 -1 8
0 8 10 -1 9
0 9 11 -1 10
0 10 12 -1 11
2 11 -1 -1 12
1 3 4 8 13]
ct=[1 -1 -1 2 -1
1 1 -1 3 -1
1 2 -1 13 -1
0 5 13 -1 -1
1 6 -1 4 -1
1 7 -1 5 -1
1 -1 -1 6 -1
1 13 -1 9 -1
0 8 10 -1 -1
1 11 -1 9 -1
1 12 -1 10 -1
1 -1 -1 11 -1
1 3 -1 4 8]
lt=[101 38 -1 -1
63 38 24 -1
39 24 7 -1
0 18 7 -1
18 18 12 -1
30 12 16 -1
46 16 -1 -1
18 7 18 -1
0 18 18 -1
18 18 12 -1
30 12 27 -1
57 27 -1 -1
32 7 7 7]
x1=[]%源点矩阵
x2=[]%断点矩阵
x3=[]%T点
y1=[]
y2=[]
y3=[]
y4=[]
y5=[]%馈线偶
z1=[]
z2=[]
z3=[]
u=1%随机变量用时重赋值
v=1%随机变量用时重赋值
v=1
g=1
for a=1:1:13
if dt(a,1)==2
x1(1,v)=a
v=v+1
end
end
v=1
for a=1:1:13
if ct(a,1)==0
x2(1,v)=a
v=v+1
end
end
v=1
for a=1:1:13
if dt(a,1)==1
x3(1,v)=a
v=v+1
end
end

b1=ct(x2(1,1),2)
b2=ct(x2(1,1),3)%第一断点的两上源
b3=ct(x2(1,2),2)
b4=ct(x2(1,2),3)%第二断点的两上源

v=b1%从断点上开始
u=2
y1(1,1)=x2(1,1)
y1(1,2)=b1
while v>0
v=ct(v,2)
u=u+1
y1(1,u)=v
end
u=length(y1)
y1(:,[u])=[]
length1=length(y1)
v=b2%从断点上开始
u=2
y2(1,1)=x2(1,1)
y2(1,2)=b2
while v>0
v=ct(v,2)
u=u+1
y2(1,u)=v
end