一、算法思想
线性回归方程在神经网络深度学习中线性回归方程是需要掌握的最基础的式子,就是:y=wx+b,其中w,b是未知的。
神经网络就是可以通过收集大量的数据集,然后将这些数据集进行训练后得到几个较为准确的参数,训练数据集后会得到两个参数,当损失率越小,那么测试集得到的数据就越准确。
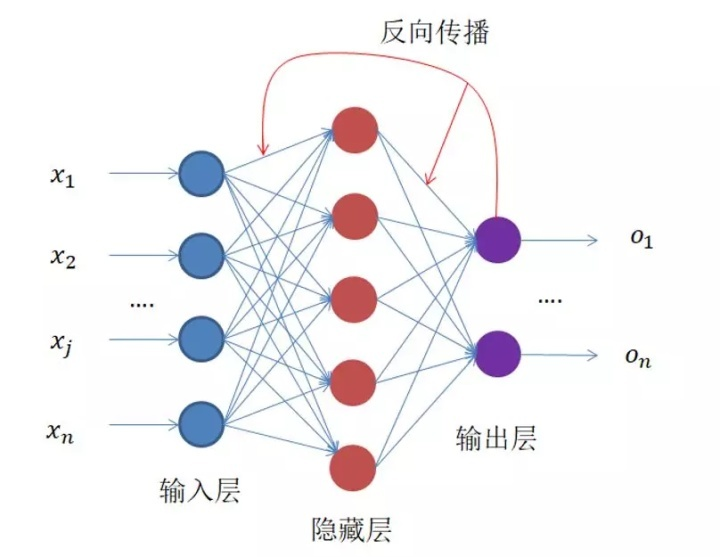
二、算法原理
在常规的神经网络中,神经网络结构中有多个层,非线性激活函数和每个节点上面的偏差单元。使用一个有一个或者多个权重w的层,在简单线性回归中,权重w和偏差单元一般都写成一个参数向量β,其中偏差单元是y轴上面的截距,w是回归线的斜率。
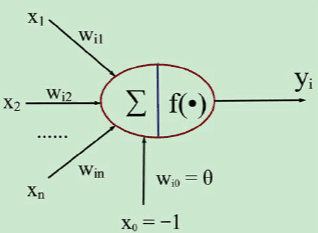
三、算法分析
(1)数据处理:即得到y和x,不过在这里称为标签和特征,之后当用更加复杂的数据以及模型的时候,则需要对其进行一些预处理来的到更好的结果
(2)构建模型:在这里的模型就是线性回归函数y = k*x+b
(3)训练模型:在这个过程中,会不断调整k和b的值来贴近真实值,具体怎么操作在之后会详细说明
(4)预测:很明显,就是通过新的x值来预测以后的y值
四、源程序代码
import numpy as np
import matplotlib.pyplot as plt
# 样本数据
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
y = [3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 10, 11, 13, 13, 16, 17, 16, 17, 18, 20]
m = 20 # 样本数量
alpha = 0.01 # 学习率
θ_0 = 1 # 初始化θ_0的值
θ_1 = 1 # 初始化θ_1的值
# 预测目标变量y的值
def predict(θ_0, θ_1, x):
y_predicted = θ_0 + θ_1 * x
return y_predicted
# 遍历整个样本数据,计算偏差,使用批量梯度下降法
def loop(m, θ_0, θ_1, x, y):
sum1 = 0
sum2 = 0
error = 0
for i in range(m):
a = predict(θ_0, θ_1, x[i]) - y[i]
b = (predict(θ_0, θ_1, x[i]) - y[i]) * x[i]
error1 = a * a
sum1 = sum1 + a
sum2 = sum2 + b
error = error + error1
return sum1, sum2, error
# 批量梯度下降法进行更新θ的值
def batch_gradient_descent(x, y, θ_0, θ_1, alpha, m):
gradient_1 = (loop(m, θ_0, θ_1, x, y)[1] / m)
while abs(gradient_1) > 0.001: # 设定一个阀值,当梯度的绝对值小于0.001时即不再更新了
gradient_0 = (loop(m, θ_0, θ_1, x, y)[0] / m)
gradient_1 = (loop(m, θ_0, θ_1, x, y)[1] / m)
error = (loop(m, θ_0, θ_1, x, y)[2] / m)
θ_0 = θ_0 - alpha * gradient_0
θ_1 = θ_1 - alpha * gradient_1
return (θ_0, θ_1, error)
θ_0 = batch_gradient_descent(x, y, θ_0, θ_1, alpha, m)[0]
θ_1 = batch_gradient_descent(x, y, θ_0, θ_1, alpha, m)[1]
error = batch_gradient_descent(x, y, θ_0, θ_1, alpha, m)[2]
print("The θ_0 is %f, The θ_1 is %f, The The Mean Squared Error is %f " % (θ_0, θ_1, error))
plt.figure(figsize=(6, 4)) # 新建一个画布
plt.scatter(x, y, label='y') # 绘制样本散点图
plt.xlim(0, 21) # x轴范围
plt.ylim(0, 22) # y轴范围
plt.xlabel('x', fontsize=20) # x轴标签
plt.ylabel('y', fontsize=20) # y轴标签
x = np.array(x)
y_predict = np.array(θ_0 + θ_1 * x)
plt.plot(x, y_predict, color='red') # 绘制拟合的函数图
plt.show()
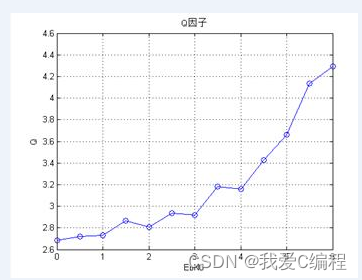
五、运行结果及分析
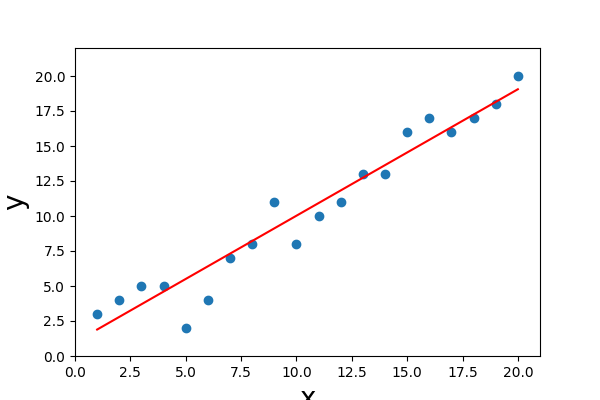
六、实验总结
线性回归的神经网络法我理解的就是对方程: 根据现有的数据来求解该方程中的w和b。
但由于实际问题中的数据x和y并不是都能被这个方程所描述,就像二维的散点图中,不能用一条直线来穿过所有的点,所以目标是要让这条直线能够穿过尽可能多的点,不在该直线上的点也能让它尽可能的离这条直线近。
即要找到合适的w和b使得计算出来的y'与真实的y误差最小化。给定训练数据特征X和对应的已知标签y,线性回归的目标是找到一组权重向量w和偏置b:
当给定从X的同分布中取样的新样本特征时, 这组权重向量和偏置能够使得新样本预测标签的误差尽可能小。