随着互联网寒潮的到来, 越来越多的互联网公司提高了面试的难度，其中之一就是加大了面试当中手撕算法题的比例。这里说的算法题不是深度学习，机器学习这类的算法，而是排序，广度优先，动态规划这类既考核数据结构也考核编程能力的题目。刷题的网址非常的多，其中以 leetcode 是最为出名的。

在刷题上，我花了大量的时间，蹚了许多的坑，总结了一下，主要有这三个问题:

刷过的题老是忘，第二次刷的时候还是不会做
刷题的速度很慢，即使花一天时间，也常常只能刷五六道
坚持不下来，老是刷到一半就停滞下来了，当我第二次再来刷的时候，前面刷过的题都又忘的差不多

说出来都是泪，感觉刷题这个路是真的难走，花了很多时间，但是感觉没有什么收获。所以最近我一直在反思自己刷题的方法，希望能够提高刷题的效率和速度。当我总结了以下方法以后，我很明显的感受到自己的刷题速度从以前周末的一天五六道提升到周末一天刷十五六道以上，速度相比以前提升的非常明显。

本文采用 Java 语言来进行描述，帮大家好好梳理一下数据结构与算法，在工作和面试中用的上。亦即总结常见的的数据结构，以及在 Java 中相应的实现方法，务求理论与实践一步总结到位。

常用数据结构

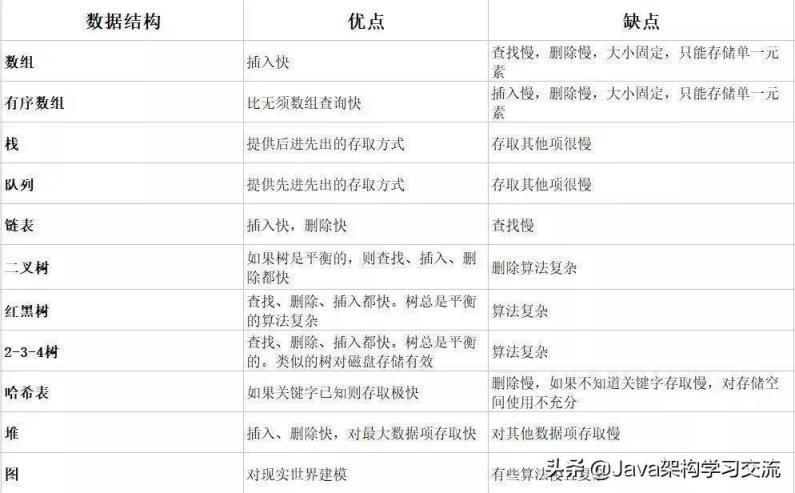
数组

数组是相同数据类型的元素按一定顺序排列的集合，是一块连续的内存空间。数组的优点是：get 和 set 操作时间上都是 O(1)的；缺点是：add 和 remove 操作时间上都是 O(N)的。

Java 中，Array 就是数组，此外，ArrayList 使用了数组 Array 作为其实现基础,它和一般的 Array 相比，最大的好处是，我们在添加元素时不必考虑越界，元素超出数组容量时，它会自动扩张保证容量。

Vector 和 ArrayList 相比，主要差别就在于多了一个线程安全性，但是效率比较低下。如今 java.util.concurrent 包提供了许多线程安全的集合类（比如 LinkedBlockingQueue），所以不必再使用 Vector 了。

链表

链表是一种非连续、非顺序的结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的，链表由一系列结点组成。链表的优点是：add 和 remove 操作时间上都是 O(1)的；缺点是：get 和 set 操作时间上都是 O(N)的，而且需要额外的空间存储指向其他数据地址的项。

查找操作对于未排序的数组和链表时间上都是 O(N)。

队列

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端进行删除操作，而在表的后端进行插入操作，亦即所谓的先进先出（FIFO）。

Java 中，LinkedList 实现了 Deque，可以做为双向队列（自然也可以用作单向队列）。另外 PriorityQueue 实现了带优先级的队列，亦即队列的每一个元素都有优先级，且元素按照优先级排序。

栈

栈（stack）又名堆栈，它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。它体现了后进先出（LIFO）的特点。

Java 中，Stack 实现了这种特性，但是 Stack 也继承了 Vector，所以具有线程安全线和效率低下两个特性，最新的 JDK8 中，推荐用 Deque 来实现栈。

集合

集合是指具有某种特定性质的具体的或抽象的对象汇总成的集体，这些对象称为该集合的元素，其主要特性是元素不可重复。

在 Java 中，HashSet 体现了这种数据结构，而 HashSet 是在 MashMap 的基础上构建的。LinkedHashSet 继承了 HashSet，使用 HashCode 确定在集合中的位置，使用链表的方式确定位置，所以有顺序。TreeSet 实现了 SortedSet 接口，是排好序的集合（在 TreeMap 基础之上构建），因此查找操作比普通的 Hashset 要快（log(N)）；插入操作要慢（log（N））,因为要维护有序。

散列表

散列表也叫哈希表，是根据关键键值(Keyvalue)进行访问的数据结构，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度，这个映射函数叫做散列函数。

Java 中 HashMap 实现了散列表，而 Hashtable 比它多了一个线程安全性，但是由于使用了全局锁导致其性能较低，所以现在一般用 ConcurrentHashMap 来实现线程安全的 HashMap（类似的，以上的数据结构在最新的 java.util.concurrent 的包中几乎都有对应的高性能的线程安全的类）。TreeMap 实现 SortMap 接口，能够把它保存的记录按照键排序。LinkedHashMap 保留了元素插入的顺序。WeakHashMap 是一种改进的 HashMap，它对 key 实行“弱引用”，如果一个 key 不再被外部所引用，那么该 key 可以被 GC 回收，而不需要我们手动删除。

树

树（tree）是包含 n（n>0）个节点的有穷集合，其中：

每个元素称为节点（node）
有一个特定的节点被称为根节点或树根（root）
除根节点之外的其余数据元素被分为 m（m≥0）个互不相交的结合 T1，T2，……Tm-1，其中每一个集合 Ti（1<=i<=m）本身也是一棵树，被称作原树的子树（subtree）

树这种数据结构在计算机世界中有广泛的应用，比如操作系统中用到了红黑树，数据库用到了 B+树，编译器中的语法树，内存管理用到了堆（本质上也是树），信息论中的哈夫曼编码等等等等，在 Java 中 TreeSet 和 TreeMap 用到了树来排序（二分查找提高检索速度），不过一般都需要程序员自己去定义一个树的类，并实现相关性质，而没有现成的 API。

下面用 Java 来实现各种常见的树。

二叉树

二叉树是一种基础而且重要的数据结构，其每个结点至多只有二棵子树，二叉树有左右子树之分，第 i 层至多有 2(i-1)个结点（i 从 1 开始）；深度为 k 的二叉树至多有 2(k)-1)个结点，对任何一棵二叉树，如果其终端结点数为 n0，度为 2 的结点数为 n2，则 n0=n2+1。

二叉树的性质：

在非空二叉树中，第 i 层的结点总数不超过 2^(i-1), i>=1;
深度为 h 的二叉树最多有 2^h-1 个结点(h>=1)，最少有 h 个结点;
对于任意一棵二叉树，如果其叶结点数为 N0，而度数为 2 的结点总数为 N2，则 N0=N2+1;
具有 n 个结点的完全二叉树的深度为 log2(n+1);
有 N 个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：若 I 为结点编号则如果 I>1，则其父结点的编号为 I/2；如果 2I<=N，则其左儿子（即左子树的根结点）的编号为 2I；若 2I>N，则无左儿子；如果 2I+1<=N，则其右儿子的结点编号为 2I+1；若 2I+1>N，则无右儿子。
给定 N 个节点，能构成 h(N)种不同的二叉树，其中 h(N)为卡特兰数的第 N 项，h(n)=C(2*n, n)/(n+1)。
设有 i 个枝点，I 为所有枝点的道路长度总和，J 为叶的道路长度总和 J=I+2i。

满二叉树、完全二叉树

满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点；

完全二叉树：若设二叉树的深度为 h，除第 h 层外，其它各层 (1～(h-1)层) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树；

满二叉树是完全二叉树的一个特例。

二叉查找树

二叉查找树，又称为是二叉排序树（Binary Sort Tree）或二叉搜索树。二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：

若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
左、右子树也分别为二叉排序树；
没有键值相等的节点。

二叉查找树的性质：对二叉查找树进行中序遍历，即可得到有序的数列。二叉查找树的时间复杂度：它和二分查找一样，插入和查找的时间复杂度均为 O(logn)，但是在最坏的情况下仍然会有 O(n)的时间复杂度。原因在于插入和删除元素的时候，树没有保持平衡。我们追求的是在最坏的情况下仍然有较好的时间复杂度，这就是平衡二叉树设计的初衷。

平衡二叉树

平衡二叉树又被称为 AVL 树，具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树。它的出现就是解决二叉查找树不平衡导致查找效率退化为线性的问题，因为在删除和插入之时会维护树的平衡，使得查找时间保持在 O(logn)，比二叉查找树更稳定。

堆

堆是一颗完全二叉树，在这棵树中，所有父节点都满足大于等于其子节点的堆叫大根堆，所有父节点都满足小于等于其子节点的堆叫小根堆。堆虽然是一颗树，但是通常存放在一个数组中，父节点和孩子节点的父子关系通过数组下标来确定。

堆的用途：堆排序，优先级队列。此外由于调整代价较小，也适合实时类型的排序与变更。