一 二叉树的五大性质

• 性质一：对于一颗二叉树，第i层的最大结点数量为
  $$2^{i-1}$$

• 性质二：对于一颗深度为k的二叉树，可以具有的最大结点数量为:
  $$n=2^0+2^1+2^2+...+2^{k-1}$$
  简化计算
  $$S_n=\frac{a_1\times (1-q^n)}{1-q}=\frac{1\times (1-2^k)}{1-2}=-(1-2^k)=2^k-1$$

  • 结论：
    • 一颗深度为k的二叉树最大结点数量为$2^k-1$,结点的边数为$E=n-1$

• 性质三：【记忆】
  $$n_0=n_2+1$$

  • 假设一颗二叉树中度为0、1、2的结点数量为$n_0、n_1、n_2$，由于一棵树二叉树中只有这三种类型的结点，可得结点总数：
    $$n=n_0+n_1+n_2$$
  • 从二叉树的边数考虑，因为每个结点有且仪有一条边与具交结点相连，那么边数之和就可以表示为
    $$E=n_1+2n_2$$
  • 度为1的结点有一条边，度为2的结点有两条边，度为0的结点没有，加在一起就是整棵二叉树的边数之和,可得
    $$E=n-1=n_1+2n_{2}n=n_1+2n_2+1$$
  • 再结合第一个公式
    $$n_0=n_2+1$$

• 性质四：【记忆】

  • 完全二叉树除了最后一层有空缺外，其他层数都是饱满的，假设这模二叉树为满二叉树，那么根据我们前面得到的性质，假设层数为$k$，那么结点数量为：$n=2^k-1$，根据完全二叉树的性质，最后一层可以满可以不满，那么一棵完全二叉树结点数$n$满足：
    $$2^{k-1}-1<n<=2^k-1$$
  • 因为n肯定是一个整数，那么可以写为
    $$2^{k-1}<=n<=2^k-1$$
  • 现在我们只看左边的不等式，我们对不等式两边同时取对数，得到
    $$k-1<=lo{g}_{2}n$$
  • 综上所述，一棵具有n个结点的完全二叉树深度为
    $$k=\lfloor lo{g}_{2}n\rfloor +1$$

• 性质五：

  • 一颗有n个结点的完全二叉树，由性质四得到深度为k=log2+1现在对于任意一个结点i，结点的顺序为从上往
    下，从左往右：
  • 对于一个拥有左右孩子的结点来说，其左孩子为$$2i$$，右孩子为$$2i+1$$
  • 如果$i=1$，那么此节点为二叉树的根节点，如果$i>1$，那么其父节点为$\lfloor i/2\rfloor$
  • 如果$2i>n$，则结点$i$没有左孩子
  • 如果$2i+1>n$，则结点i没有右孩子

二 判断题

1. 若二叉树用二叉链表作存贮结构，则在n个结点的二叉树链表中只有$n-1$个非空指针域。（ √ ）
   • 解析：$n$个结点的二叉树，总共有$n-1$条边，其对应的二叉链表的非空指针个数等于二叉树的边数$n-1$,所以答案正确。
2. 二叉树中每个结点的两棵子树的高度差等于1。 （ × ）
   • 解析：
     • 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
     • 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。
     • 这是个平衡二叉树的定义，而不是普通二叉树的要求
3. 二叉树中每个结点的两棵子树是有序的。 （ √ ）
   • 解析：二叉树每个结点的左右子树都有特殊含义【左子树表示其孩子，右子树表示其兄弟】，所以答案正确。
4. 二叉树中每个结点有两棵非空子树或有两棵空子树。 （ × ）
   • 解析：二叉树中允许存在结点有一颗非空子树【完全二叉树】
5. 二叉树中每个结点的关键字值大于其左非空子树（若存在的话）所有结点的关键字值，且小于其右非空子树（若存在的话）所有结点的关键字值。 ( × ）
   • 解析：二叉排序树的特点
6. 二叉树中所有结点个数是$2^{k-1}-1$，其中$k$是树的深度。 （ × ）
   • 解析：由二叉树的性质二可知，树的深度应为$k-1$
7. 二叉树中所有结点，如果不存在非空左子树，则不存在非空右子树。 （ × ）
   • 解析：二叉树中的结点可以不存在左子树【孩子结点】，同时存在右子树【兄弟结点】
8. 对于一棵非空二叉树，它的根结点作为第一层，则它的第i层上最多能有$2^i-1$个结点。（ × ）
   • 解析：由性质一可得，应为$2^{i-1}$
9. 用二叉链表法（link-rlink）存储包含n个结点的二叉树，结点的2n个指针区域中有n+1个为空指针。（ √ ）
   • 解析：用二叉链表存储包含n个结点的二叉树，结点共有$2n$个链域。由于二叉树中，除根结点外，每一个结点有且仅有一个双亲，所以只有$n-1$个结点的链域存放指向非空子女结点的指针，还有$n+1$个空指针。）即有后继链接的指针仅$n-1$个。
10. 具有12个结点的完全二叉树有5个度为2的结点。（ √ ）
    • 解析：叶子数＝$\lceil n/2\rceil$＝6[向上取整]，再求$n_2=n_0-1=5$
11. 一颗完全二叉树有1001个结点，其叶子节点的个数为500（×）
    • 解析：
      • 既然是完全二叉树，那么最下面这一排肯定是按顺序排的，并且上面各层应该是排满了的，那么我们先求出层数，根据性质四
        $$k=lo{g}_{2}n+1=9+1=10$$
    • 所以此二叉树的层数为10，也就是说上面9层都是满满当当的，最后一层不满，那么根据性质二，我们求出前9层的结点数
      $$n=2^k-1=511$$
    • 那么剩下的结点就都是第十层的了，得到$第十层所有叶子结点数量=1001-511=490$，因为第十层并不满，剩下的叶子第九层也有，所以最后我们还需要求出第九层的叶子结点数量，先计算第九层的所有结点数量
      $$n=2^{i-1}=256$$
    • 接着我们需要去掉那些第九层度为一和度为二的结点，其实只需要让第十层都叶子结点除以2就行
      $$n=（490+1）/2=245$$

注意在除的时候+1，因为有可能会出现一个度为1的结点，此时也需要剔除，所以说+1变成偶数这样才可以正确得到结果。最后剔除这些结点，得到最终结果

$$n_0=256-245+490=501$$

• 深入研究
  • 探索：
    • 设叶子节点个数为$n_0$,度为$1$的节点个数为$n_1$,度为$2$的节点个数为$n_2$侧有
      $$n_0+n_1+n_2=n$$
    • 对于二叉树有：
      $$n_0=n_2+1$$
    • 可得
      $$n_0=(n+1-n_1)/2$$
    • 由完全二叉树的性质可知：$n_1=0或1$
    • 总结:
      1. 当n1=0时(即度为1的节点为0个时,此时n为奇数）或者n为奇数时
         $$n_0=(n+1)/2$$
      2. 当n1=1时(即度为1的节点为1个时,此时n为偶数）或者n为偶数
         $$n_0=n/2$$
      3. 一个具有$n$个节点的完全二叉树,其叶子节点的个数$n_0$为: $\lceil n/2\rceil$ 向上取整或者 $\lfloor (n+1)/2\rfloor$向下取整

12. 一颗1025个结点的二叉树的层数$k$的层数范围为$11-1205$（ √ ）
    • 解析：根据性质四可得最小深度为$\lfloor lo{g}_{2}n\rfloor +1=11$,最大的深度为1005【每层只一个结点】
13. 由一棵树转化而来的二叉树，根节点无右子树。由森林转化而来的二叉树，根节点由有右子树。( √ )
    • 解析：一棵树根节点没有兄弟节点，森林中的每棵树的根节点互为兄弟节点。

三 填空题

1. 由３个结点所构成的二叉树有***（5 ）***种形态。
   

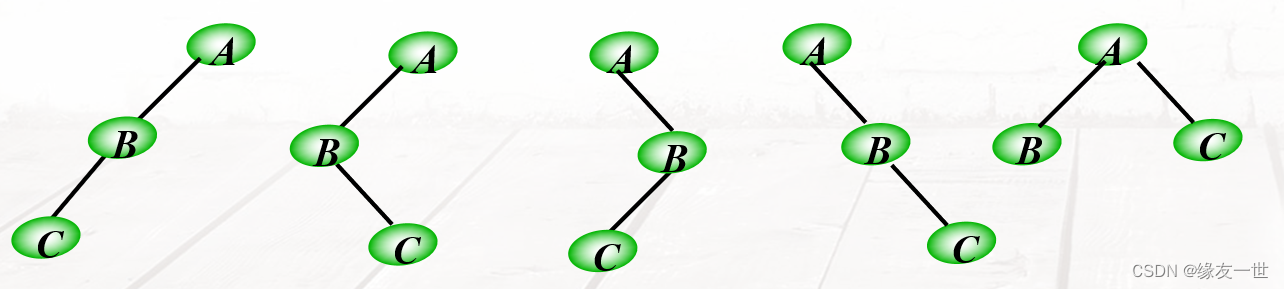
• 深入研究：

  • 如果是$N$个结点的话，利用动态规划进行解答，分析如下：
  • 假设现在只有一个结点或者没有结点、那么只有一种，$h(0)=h(1)=1$
  • 假设现在有两个结点，那么其中一个拿来做根结点，剩下这一个可以左边可以右边，要么左边零个结点右边一个结点，要么左边一个结点右边零个结点，所以说$h(2)=h(1)\times h(0)+h(0)xh(1)=2$
  • 假设现在有三个结点，那么依然是其中一个拿来做根节点，剩下的两个结点情况就多了，要么两个都在左边，两个都在右边，或者一边一个，所以说$h(3)=h(2)xh(0)+h(1)xh(1)+h(1)\times h(2)$
  • 规律:$N每+1$，项数多一项，所以我们只需要按照规律把所有情况的结果相加

  int main() {
      int size;
      cout<<"请输入结点的总个数:";
      cin>>size;
      int dp[size+1];
      dp[0]=dp[1]=1;//没有节点或者只有一个结点直接得到1
      for(int i=2;i<=size;i++) {//从2开始进行叠加的计算
          dp[i]=0;//一开始
          //内层循环，计算所有的情况，如i=3,计算dp[0]*dp[2],dp[1]*dp[1],dp[2]*dp[0]
          for(int j=0;j<i;j++) {
              dp[i]+=dp[j]*dp[i-j-1];
          }
      }
      cout<<"二叉树的种类总数为:"<<dp[size]<<endl;
      return 0;
  }
  

  

  • 这个数列其实其卡特兰数，其通项公式为：
    $$C_n=\frac{1}{n+1}{C}_{2n}^n=\frac{1}{n+1}\times \frac{(2n)!}{n!\times (2n-n)!}=\frac{(2n)!}{n!\times (n+1)!}$$

  int factorial(int n) {
    int res=1;
    for(int i=2;i<=n;i++) res*=i;
    return res;
  	}
  int main() {
      int n;
      cout<<"请输入结点的总个数:";
      cin>>n;
      cout<<"二叉树的种类总数为:";
      cout<<factorial(2*n)/(factorial(n)* factorial(n+1));
      return 0;
  }
  

  

2. 一棵深度为6的满二叉树有 (31) 个分支结点和 (32) 个叶子。

• 解析：
  • 满二叉树没有度为$1$的结点，所以分支结点数就是度$2$为结点数。
  • 满二叉树的最后一层的结点都是叶子节点，个数为$n_0=2^{6-1}=32$
  • 分支结点的个数为$n_1+n_2=0+n_2=n_0-1=31$

3. 一棵具有$257$个结点的完全二叉树，它的深度为 (9) 。

   • 解析：$\lfloor lo{g}_2(n)\rfloor +1=8+1=9$

4. 设一棵完全二叉树有700个结点，则共有 (350) 个叶子结点。

   • 解析：$\lceil n/2\rceil ＝350$

5. 设一棵完全二叉树具有1000个结点，则此完全二叉树有 (500) 个叶子结点，有 (499) 个度为2的结点，有 (1) 个结点只有非空左子树，有 (0) 个结点只有非空右子树。

   • 解析：用叶子数$\lceil n/2\rceil ＝500$ ，$n_2=n_0-1=499$。 另外，最后一结点为$2i$属于左叶子，右叶子是空的，所以有1个非空左子树。完全二叉树的特点决定不可能有左空右不空的情况，所以非空右子树数＝$0$.

6. 【有坑】一棵含有n个结点的k叉树，可能达到的最大深度为 n ，最小深度为 2 。

   • 解析：
   • 当$k=1$(单叉树)时应该最深，深度＝n（层）；
   • 当$k=n-1$（n-1叉树）时应该最浅，深度＝2（层），但不包括n=0或1时的特例情况.
   • 类似的题目：
     • 深度为$h$的满$m$叉树的第$k$层有多少个结点?
     • 类比于二叉树的性质一，可得$n=m^{k-1}$

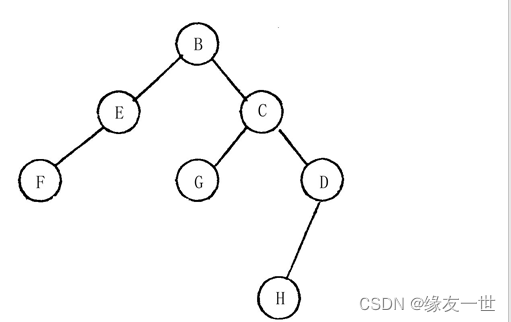
7. 二叉树的基本组成部分是：根（N）、左子树（L）和右子树（R）。因而二叉树的遍历次序有六种。最常用的是三种：前序法（即按N L R次序），后序法（即按 L R N 次序）和中序法（也称对称序法，即按L N R次序）。这三种方法相互之间有关联。若已知一棵二叉树的前序序列是BEFCGDH，中序序列是FEBGCHD，则它的后序序列必是 F E G H D C B 。

   • 解析：先由已知条件画图，再后序遍历得到结果；
     

8. 中序遍历的递归算法平均空间复杂度为 $O(n)$ 。
   -解析：即递归最大嵌套层数，即栈的占用单元数。精确值应为树的深度$k+1$，包括叶子的空域也递归了一次。

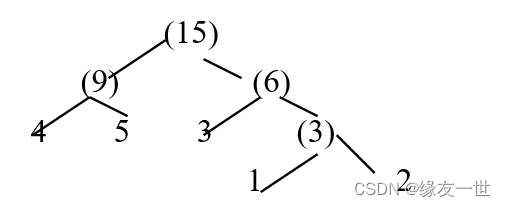
9. 用5个权值{3, 2, 4, 5, 1}构造的哈夫曼（Huffman）树的带权路径长度是 33 。

   • 解析：先构造哈夫曼树，得到各叶子的路径长度之后便可求出WPL＝（4＋5＋3）×2＋（1＋2）×3=33
     

四 选择题

1. 不含任何结点的空树 （ C ） 。
   （Ａ）是一棵树; （Ｂ）是一棵二叉树;
   （Ｃ）是一棵树也是一棵二叉树; （Ｄ）既不是树也不是二叉树

2. 二叉树是非线性数据结构，所以 （ C ） 。
   （Ａ）它不能用顺序存储结构存储; （Ｂ）它不能用链式存储结构存储;
   （Ｃ）顺序存储结构和链式存储结构都能存储; （Ｄ）顺序存储结构和链式存储结构都不能使用

3. 具有n(n>0)个结点的完全二叉树的深度为 （ C ） 。
   (Ａ) $\lceil lo{g}_2(n)\rceil$
   (Ｂ) $\lfloor log2(n)\rfloor$
   (Ｃ) $\lfloor log2(n)\rfloor$+1
   (Ｄ) $\lceil lo{g}_2(n)+1\rceil$

• 解析：由性质四即可解答

4. 把一棵树转换为二叉树后，这棵二叉树的形态是 （ A ） 。
   （Ａ）唯一的 （Ｂ）有多种
   （Ｃ）有多种，但根结点都没有左孩子 （Ｄ）有多种，但根结点都没有右孩子

5. 树是结点的有限集合，它A 根结点，记为T。其余的结点分成为m（m≥0）个 B 的集合T1，T2，…，Tm，每个集合又都是树，此时结点T称为Ti的父结点，Ti称为T的子结点（1≤i≤m）。一个结点的子结点个数为该结点的 C 。
   供选择的答案

• A：
  • ①有0个或1个
  • ②有0个或多个
  • ③有且只有1个
  • ④有1个或1个以上
• B:
  • ①互不相交
  • ② 允许相交
  • ③ 允许叶结点相交
  • ④ 允许树枝结点相交
• C：
  • ①权
  • ② 维数
  • ③ 次数（或度）
  • ④ 序
• 解析：ABC＝1，1，3

6. 二叉树 A 。在完全的二叉树中，若一个结点没有 B ，则它必定是叶结点。每棵树都能惟一地转换成与它对应的二叉树。由树转换成的二叉树里，一个结点N的左子女是N在原树里对应结点的 C ，而N的右子女是它在原树里对应结点的 D 。

• A：
  • ①是特殊的树
  • ②不是树的特殊形式
  • ③是两棵树的总称
  • ④有是只有二个根结点的树形结构
• B:
  • ①左子结点
  • ② 右子结点
  • ③ 左子结点或者没有右子结点
  • ④ 兄弟
• C～D：
  • ①最左子结点
  • ② 最右子结点
  • ③ 最邻近的右兄弟
  • ④ 最邻近的左兄弟
  • ⑤ 最左的兄弟
  • ⑥ 最右的兄弟
• 答案：ABCDE＝2，1，1，3

四 分析求解题

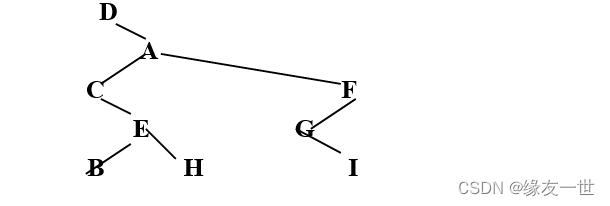
1. 给定二叉树的两种遍历序列，分别是：前序遍历序列：D，A，C，E，B，H，F，G，I； 中序遍历序列：D，C，B，E，H，A，G，I，F，试画出二叉树B。
   
2. 给定如图所示二叉树T，请画出与其对应的中序线索二叉树。
   

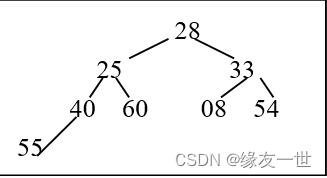
• 解：要遵循中序遍历的轨迹来画出每个前驱和后继。
  • 中序遍历序列：55 40 25 60 28 08 33 54

3. 试写出如图所示的二叉树分别按先序、中序、后序遍历时得到的结点序列。
   

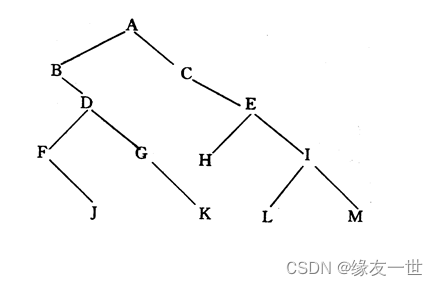
• 前序DLR：A B D F J G K C E H I L M
• 中序LDR: B F J D G K A C H E L I M
• 后序LRD：J F K G D B H L M I E C A

4. 把如图所示的树转化成二叉树
   

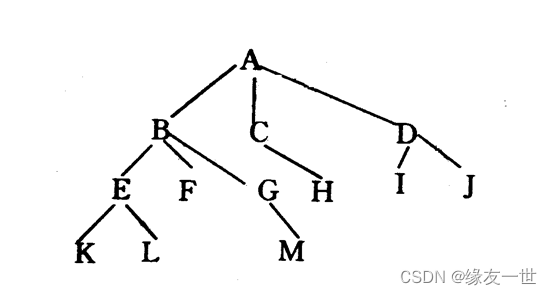
• 解答
  
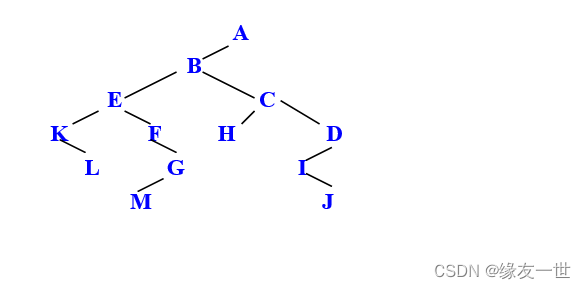
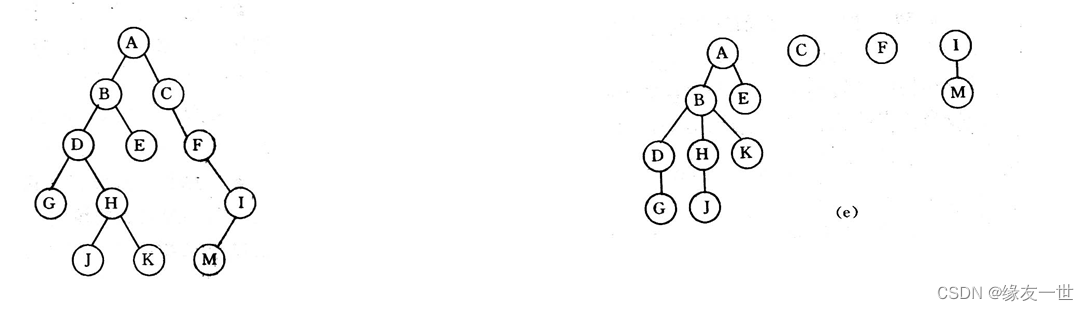
  5．画出和下列二叉树相应的森林。
  答：注意根右边的子树肯定是森林，而孩子结点的右子树均为兄弟。
  

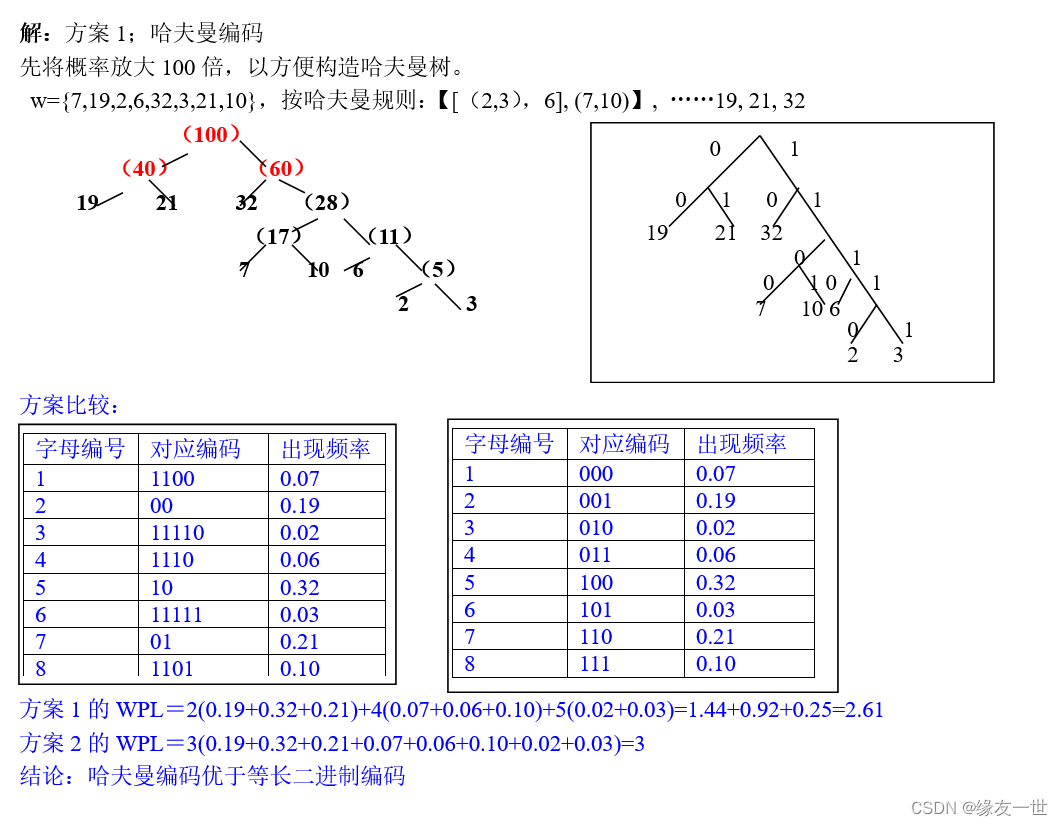
6. 假设用于通信的电文仅由8个字母组成，字母在电文中出现的频率分别为0.07，0.19，0.02，0.06，0.32，0.03，0.21，0.10。试为这8个字母设计哈夫曼编码。使用0～7的二进制表示形式是另一种编码方案。对于上述实例，比较两种方案的优缺点。
   

五 算法设计题

1. 编写递归算法，计算二叉树中叶子结点的数目。
   思路：输出叶子结点比较简单，用任何一种遍历递归算法，凡是左右指针均空者，则为叶子，将其打印出来。
   法一：核心部分为：

DLR(liuyu *root)     /*中序遍历   递归函数*/
{ if (root!=NULL)
 { if ((root->lchild==NULL)&&(root->rchild==NULL)){sum++; printf ("%d\n",root->data);}
  DLR (root->lchild);
  DLR (root->rchild); }
 Return (0);
}
法二：
int LeafCount_BiTree(Bitree T)//求二叉树中叶子结点的数目 
{ 
  If (!T) return 0; //空树没有叶子 
  else if (!T->lchild&&!T->rchild) return 1; //叶子结点 
  else return Leaf_Count(T->lchild)+Leaf_Count(T->rchild);//左子树的叶子数加 
上右子树的叶子数 
}//LeafCount_BiTree 

2. 写出求二叉树深度的算法。
   设计思路：只查后继链表指针，若左或右孩子的左或右指针非空，则层次数加1；否则函数返回。
   但注意，递归时应当从叶子开始向上计数，否则不易确定层数。

int depth(liuyu*root)     /*统计层数*/
{
	int d,p;                   /*注意每一层的局部变量d,p都是各自独立的*/
	p=0;
	if(root==NULL)return(p);      /*找到叶子之后才开始统计*/
	else{ 
		d=depth(root->lchild);
		if(d>p) p=d;              /*向上回朔时，要挑出左右子树中的相对大的那个深度值*/
		d=depth(root->rchild);
		if(d>p)p=d;
	}
	p=p+1;
	return(p);
}

法二：

int Get_Sub_Depth(Bitree T,int x)//求二叉树中以值为x的结点为根的子树深度 
{ 
  if(T->data==x) 
  { 
    printf("%d\n",Get_Depth(T)); //找到了值为x的结点,求其深度 
    exit 1; 
  } 
  } 
  else 
  { 
    if(T->lchild) Get_Sub_Depth(T->lchild,x); 
    if(T->rchild) Get_Sub_Depth(T->rchild,x); //在左右子树中继续寻找 
  } 
}//Get_Sub_Depth 
int Get_Depth(Bitree T)//求子树深度的递归算法 
{ 
  if(!T) return 0; 
  else 
  { 
    m=Get_Depth(T->lchild); 
    n=Get_Depth(T->rchild); 
    return (m>n?m:n)+1; 
  } 
}//Get_Depth 

3. 编写按层次顺序（同一层自左至右）遍历二叉树的算法。
   思路：既然要求从上到下，从左到右，则利用队列存放各子树结点的指针是个好办法。
   这是一个循环算法，用while语句不断循环，直到队空之后自然退出该函数。
   技巧之处：当根结点入队后，会自然使得左、右孩子结点入队，而左孩子出队时又会立即使得它的左右孩子结点入队，……以此产生了按层次输出的效果。

Level (liuyu*T)
/* liuyu *T,*p,*q[100];   假设max已知*/
{
	int f,r;
	f=0; r=0;             /*置空队*/
	r=(r+1)%max;
	q[r]=T;             /*根结点进队*/
	while(f!=r)        /*队列不空*/
	{
		f=(f+1%max);
		p=q[f];            /*出队*/
		printf("%d",p->data);         /*打印根结点*/
		if(p->lchild){r=(r+1)%max; q[r]=p->lchild;}     /*若左子树不空，则左子树进队*/     
		if(p->rchild){r=(r+1)%max; q[r]=p->rchild;}     /*若右子树不空，则右子树进队*/     
	}
	return(0);
}

法二：

void LayerOrder(Bitree T)//层序遍历二叉树 
{ 
  InitQueue(Q); //建立工作队列 

  EnQueue(Q,T); 
  while(!QueueEmpty(Q)) 
  { 
    DeQueue(Q,p); 
    visit(p); 
    if(p->lchild) EnQueue(Q,p->lchild); 
    if(p->rchild) EnQueue(Q,p->rchild); 
  } 
}//LayerOrder 

4. 编写算法判别给定二叉树是否为完全二叉树。

int IsFull_Bitree (Bitree T)//判断二叉树是否完全二叉树,是则返回1,否则返回0 
{ 
  InitQueue(Q); 
  flag=0; 
  EnQueue(Q,T); //建立工作队列 
  while(!QueueEmpty(Q)) 
  { 
  { 
    DeQueue(Q,p); 
    if(!p) flag=1; 
    else if(flag) return 0; 
    else 
    { 
      EnQueue(Q,p->lchild); 
      EnQueue(Q,p->rchild); //不管孩子是否为空,都入队列 
    } 
  }//while 
  return 1; 
}//IsFull_Bitree 

分析：该问题可以通过层序遍历的方法来解决.与6.47相比,作了一个修改,不管当前结点 是否有左右孩子,都入队列.这样当树为完全二叉树时,遍历时得到是一个连续的不包含空 指针的序列.反之,则序列中会含有空指针.