目录

DEFINITION 2.3 完美保密加密方案的定义

LEMMA 2.5 完美保密方案的等价定义(一)

LEMMA 2.7 完美保密方案的等价定义(二)

三个等价定义的通俗描述

等价性的证明（手写过程）

---

DEFINITION 2.3 完美保密加密方案的定义

一个在明文空间M上的加密方案（Gen，Enc，Dec），如果对于每个明文 m ∈ M，对每个密文c ∈ C，其中Pr[C=c]>0，有：

Pr[ M = m | C = c ] = Pr[ M = m ]

则称这种加密方案是完美保密

LEMMA 2.5 完美保密方案的等价定义(一)

一个在明文空间M上的加密方案是完美保密的，当且仅当，对于每个明文m，m‘ ∈ M，以及每个密文 c ∈ C有：（即加密不同的明文得到相同的密文的概率是一样的，这个概率是通过遍历密钥空间得出来的）

LEMMA 2.7 完美保密方案的等价定义(二)

一个在明文空间M上的加密方案：Π = (Gen, Enc, Dec)是完美不可区分的，当且仅当对每个敌手A都有：

 一个加密方案 Π 是完美保密的，当且仅当它是完美不可区分的。

---

三个等价定义的通俗描述

定义一：密文中无法得到关于明文的任何信息，明文的后验概率等于明文的先验概率。明文和密文存在统计独立关系，明密文之间的互信息为0，攻击者分析密文的统计规律无法得到关于明文的信息。

Pr[ M = m | C = c ] = Pr[ M = m ]

定义二：密文的分布不依赖与明文，不管明文是m还是m’，得到的密文分布是相同的。还是说明明文和密文存在统计独立关系。

 

定义三：m是m0或者m1的概率都是0.5，任意选择m并加密为c后，敌手根据c判断m是m0还是m1，概率仍然是0.5。敌手没有从密文中获取任何有用的信息 

 

 

---

等价性的证明（手写过程）

先证明定义2.3和引理2.5是等价的

 再证明定义2.3和引理2.7是等价的

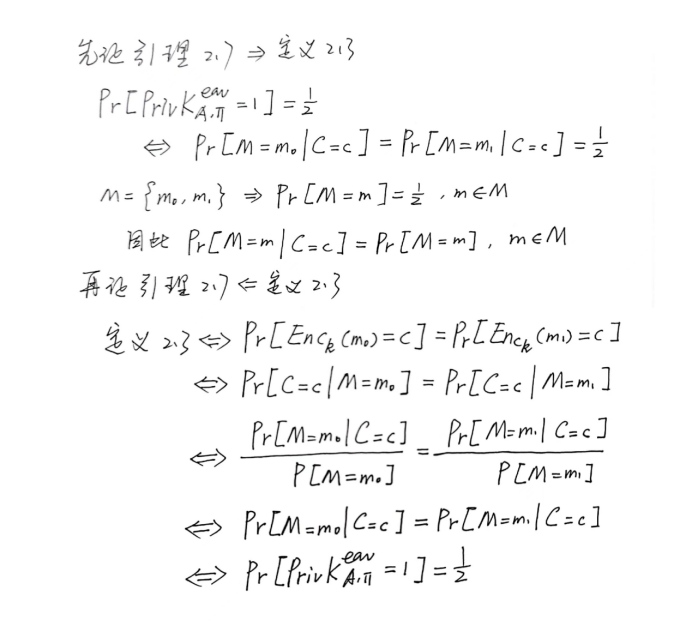
证明涉及到概率论相关知识，可参考本书附录A.3

IMC附录A_南鸢北折的博客-CSDN博客