一、实验内容
- 掌握基于密度的聚类方法的基本思想;
- 掌握单变量函数的梯度下降的原理、算法及python实现;
- 掌握双变量函数的梯度下降的原理、算法及python实现,并测试分析;
- 理解学习率η的选择并测试分析。
二、实验过程
1、算法思想
在机器学习中应用十分的广泛,不论是在线性回归还是逻辑回归中,它的主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值。
2、算法原理
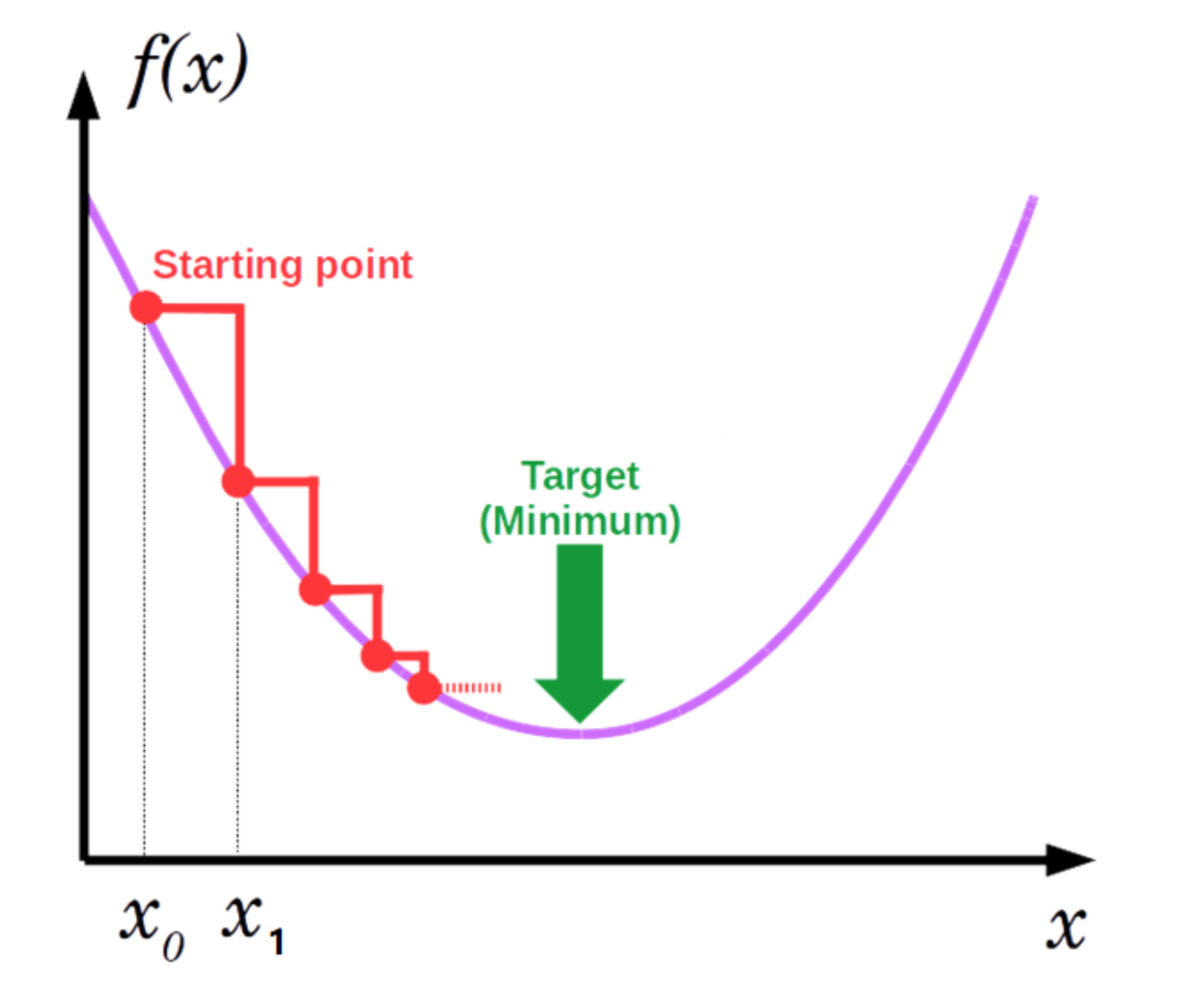
梯度下降的基本过程就和下山的场景很类似。首先,我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值,也就是山底。
根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向。
3、算法分析
从第0个到第i个训练数据的个数:
(1)计算第 i 个训练数据的权重和偏差 b 相对于损失函数的梯度。于是我们最终会得到每一个训练数据的权重和偏差的梯度值。
(2)计算当前所有训练数据权重的梯度的总和。
(3)计算当前所有训练数据偏差的梯度的总和。
做完上面的计算之后,我们开始执行下面的计算:
使用上面第(2)、(3)步所得到的结果,计算所有样本的权重和偏差的梯度的平均值。
使用下面的式子,更新每个样本的权重值和偏差值。

重复上面的过程,直至损失函数收敛不变。
三、源程序代码
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
# 目标函数
def f(x, y):
return x ** 2 + y ** 2 + x * y
# 对x求偏导
def partial_x(x, y):
return 2 * x + y
# 对y求偏导
def partial_y(x, y):
return 2 * y + x
X = np.arange(-10, 10, 1)
Y = np.arange(-10, 10, 1)
X, Y = np.meshgrid(X, Y)
Z = f(X, Y)
# 绘制曲面
fig = plt.figure()
ax = Axes3D(fig,auto_add_to_figure=False)
fig.add_axes(ax)
surf = ax.plot_wireframe(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.viridis)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
# 随机初始点
x = 8
y = 5
z = f(x, y)
next_x = x
next_y = y
xlist = [x]
ylist = [y]
zlist = [z]
# 设定一个学习率
step = 0.01
while True:
next_x = x - step * partial_x(x, y)
next_y = y - step * partial_y(x, y)
next_z = f(next_x, next_y)
print(next_x,next_y,next_z)
# 小于阈值时,停止下降
if z - next_z < 1e-9:
break
x = next_x
y = next_y
z = f(x, y)
xlist.append(x)
ylist.append(y)
zlist.append(z)
ax.plot(xlist, ylist, zlist, 'r--')
plt.show()四、运行结果及分析
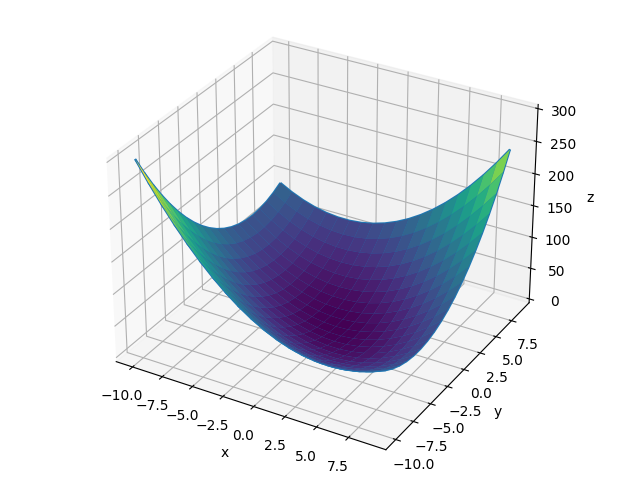
五、实验总结
梯度下降法实现简单,当目标函数是凸函数时,梯度下降法的解是全局解。
缺点:靠近极小值时收敛速度减慢,求解需要很多次的迭代;
一般情况下,其解不保证是全局最优解,梯度下降法的速度也未必是最快的。






![[注塑]各种进胶方式优缺点分析](https://img-blog.csdnimg.cn/d415d6f71c2c4f979a43d90bda07a8b9.png)


![[Spring Cloud] GateWay自定义过滤器/结合Nacos服务注册中心](https://img-blog.csdnimg.cn/fb4fe2cccab34b23b8f372e5850e2ef4.png)
