01背包、完全背包、多重背包、分组背包总结

文章目录

- 一、01背包问题
- 二、完全背包问题
- 三、多重背包问题
- 四、分组背包

一、01背包问题

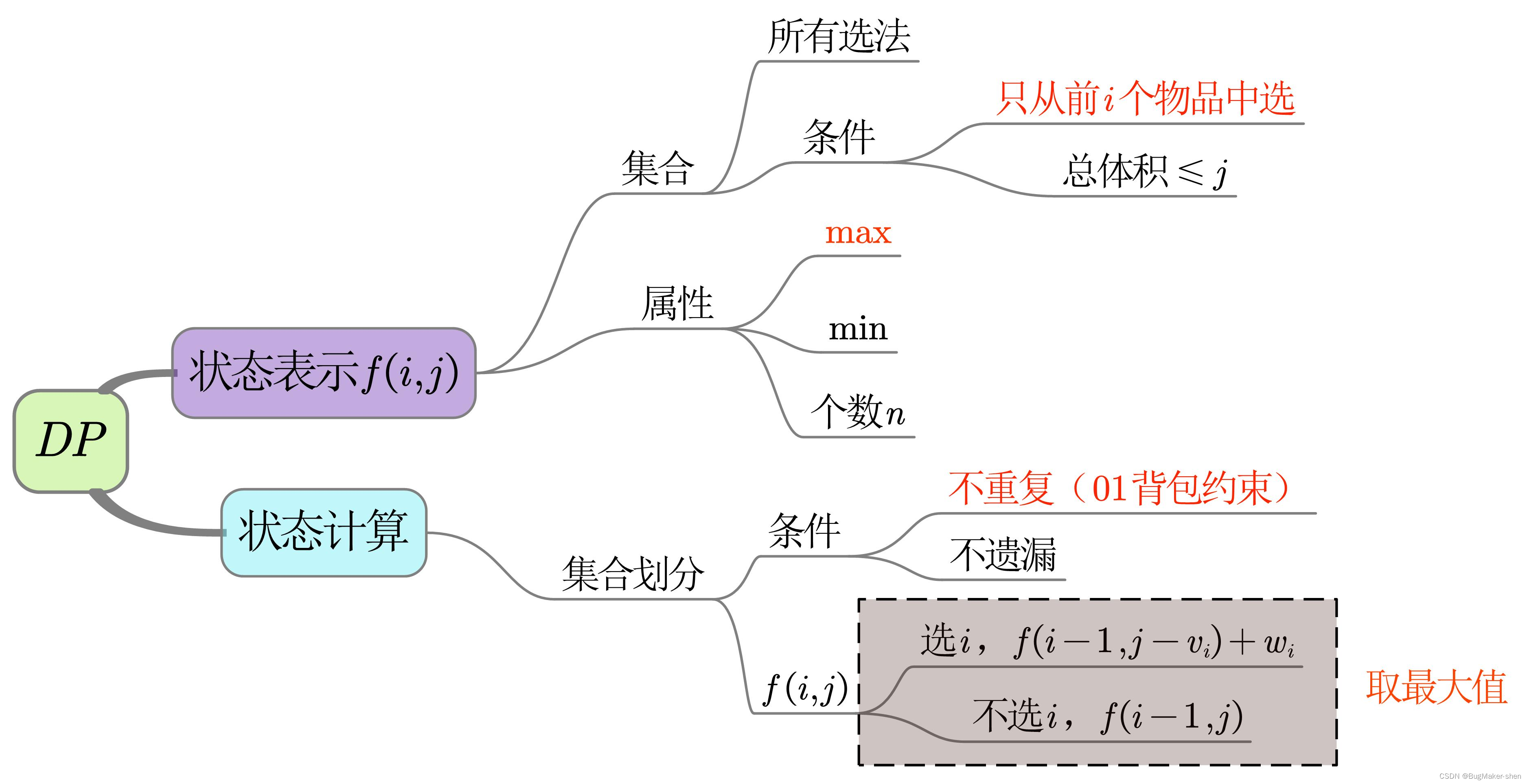
在这里插入图片描述

n个物品，每个物品的重量是 $w_i$ ，价值是 $v_i$ ，背包的容量是 $m$

若每个物品最多只能装一个，且不能超过背包容量，则背包的最大价值是多少？

模板

int n;              // 物品总数
int m;              // 背包容量
int v[n];           // 价值 
int w[n];           // 重量

二维形式

// f[i][j]表示在考虑前i个物品后，背包容量为j条件下的最大价值
int f[n][m];
// 先遍历物品，后遍历容量
for(int i = 1; i <= n; ++i){
	for(int j = 1; j <= m; ++j){
		if(j < w[i]) f[i][j] = f[i-1][j];   //  当前重量装不进，价值等于前i-1个物品   
        else f[i][j] = max(f[i-1][j], f[i-1][j-w[i]] + v[i]); // 能装，需判断  
	}
}
cout << f[n][m];

一维形式

int f[m];   // f[j]表示背包容量为j条件下的最大价值
for(int i = 1; i <= n; ++i) 
    for(int j = m; j >= w[i]; --j)
        f[j] = max(f[j], f[j - w[i]] + v[i]);           // 注意是倒序，否则出现写后读错误
cout << f[m];           // 注意是m不是n

注意f[i][j]的含义：在考虑前i个物品后，背包容量为j条件下的最大价值。而不是表示选了i个物品的最大价值，实际上选择的物品数<=i。f[j]表示背包容量为j条件下的最大价值

二维压缩成一维，实际上是寻找避开写后读错误的方法:

f[i][j]始终只用上一行的数据f[i-1][...]更新（迭代更新的基础，如果还需用上上行数据则不可压缩）
f[i][j]始终用靠左边的数据f[i-1][<=j]更新（决定了只能倒序更新）

显然i=0时，f(i,j)=0，而初始化时自动赋予0，故不必但单独处理第0行

二、完全背包问题

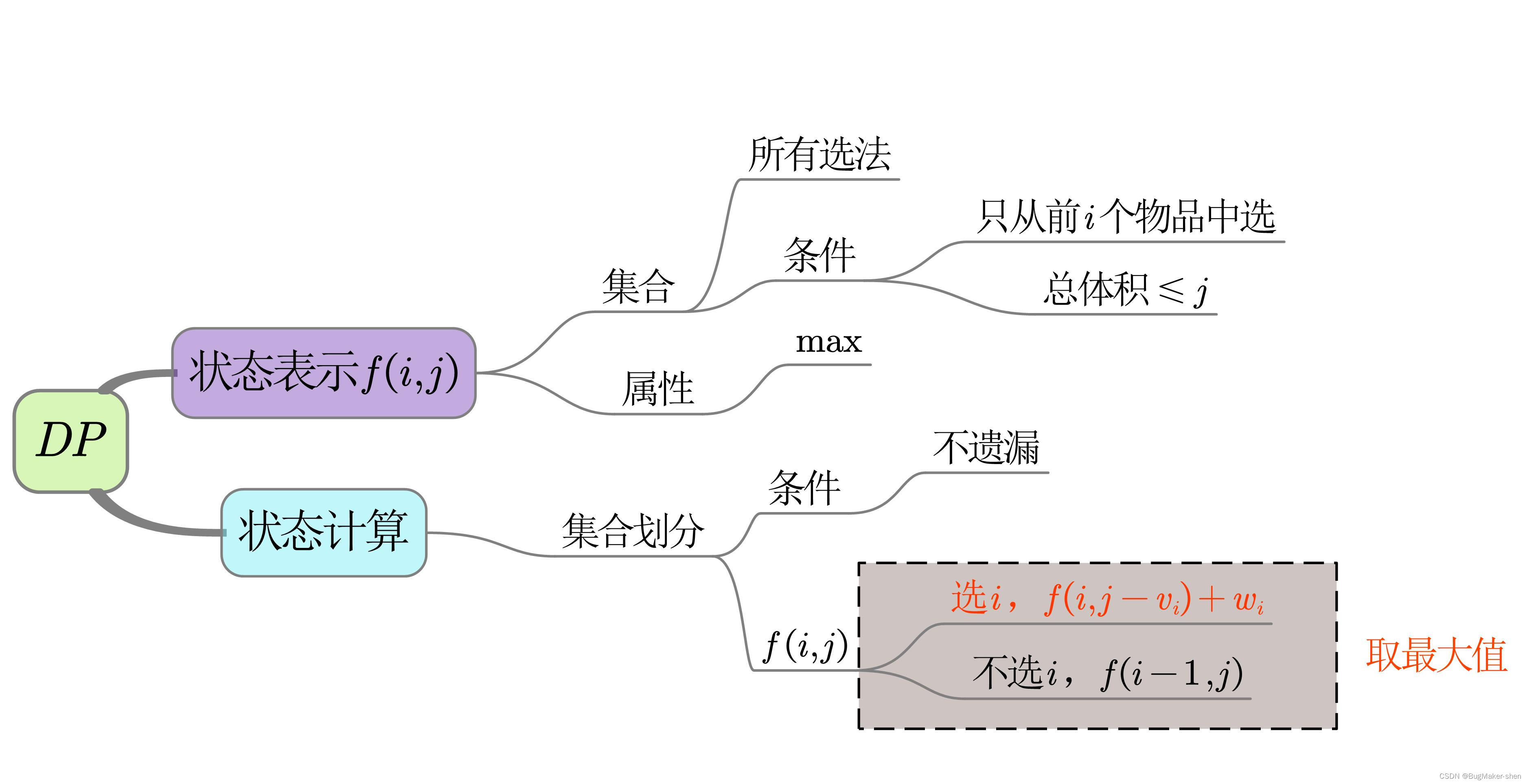
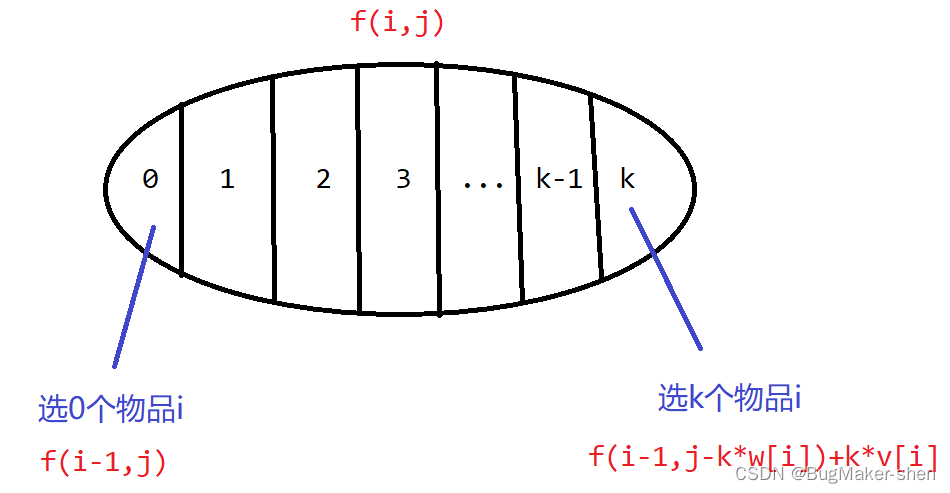
在这里插入图片描述
假设背包容量为j时，最多可装入k个物品i，k不能无限大，因为背包容量有限，则有：

$f(i,j)=max(f(i−1,j),f(i−1,j−w_i)+v_i,f(i−1,j−2w_i)+2v_i,⋯,f(i−1,j−kw_i)+kv_i)$

上述max括号里总共k+1项

考虑到：

$f(i,j−w_i)=max(f(i−1,j−w_i),f(i−1,j−2w_i)+v_i,f(i−1,j−3w_i)+2v_i,⋯,f(i−1,j−kw_i)+(k−1)v_i)$

上述max括号里总共k项

上式变形得：

$f(i,j−w_i)+v_i=max(f(i−1,j−w_i),f(i−1,j−2w_i)+v_i,f(i−1,j−3w_i)+2v_i,⋯,f(i−1,j−kw_i)+(k−1)v_i)+v_i$

因此我们得到：

$f(i,j)=max(f(i−1,j),f(i,j-w_i)+v_i)$

也就是f[i][j]可以由其左侧的f[i,j-w[i]]和其正上方的f[i−1][j]推导出来

在这里插入图片描述
未优化的二维形式

// f[i][j]表示在考虑前i个物品后，背包容量为j条件下的最大价值
int f[N][M];    
for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
    	// 第三重循环遍历上述的椭圆，找最大值，分别表示物品i取 0 ... j/w[i]次
        for (int k = 0; k <= j / w[i]; k++)
            f[i][j] = max(f[i][j], f[i - 1][j - k * w[i]] + k * v[i]);   // 注意和01背包的对比
cout << f[n][m];

// 最内层的for循环求出 f[i-1][j] , f[i-1][j-w[i]] + v[i],  f[i-1][j-2*w[i]] + 2*v[i], ..., f[i-1][j-k*w[i]] + k*v[i]中的最大值

优化的二维形式

// f[i][j]表示在考虑前i个物品后，背包容量为j条件下的最大价值
int f[N][M];    
for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
    	if(j < v[i]) f[i][j] = f[i-1][j];   //  当前重量装不进，价值等于前i-1个物品   
        else f[i][j] = max(f[i-1][j], f[i][j - w[i]] + v[i]); // max(不装物品i，装物品i(包含了装1个...装j/w[i]个的情况))  
cout << f[n][m];

// f[i][j - w[i]] + v[i] = max(装0个物品i,装1个物品i,...,装k个物品i) + v[i] 
// f[i][j - w[i]] + v[i] = max(f[i-1][j-w[i]], f[i-1][j-2*w[i]]+v[i], ..., f[i-1][j-(k+1)*w[i]]+k*v[i]) + v[i]
// f[i][j - w[i]] + v[i] = max(f[i-1][j-w[i]] + v[i], f[i-1][j-2*w[i]]+2*v[i], ..., f[i-1][j-(k+1)*w[i]]+(k+1)*v[i])
// f[i][j - w[i]] + v[i] = max(f[i-1][j-w[i]] + v[i], f[i-1][j-2*w[i]]+2*v[i], ..., f[i-1][j-(k+1)*w[i]]+(k+1)*v[i])
// f[i][j - w[i]] + v[i] = max(装1个,...,装j/w[i]个)

优化的一维形式

// f[i][j]表示在考虑前i个物品后，背包容量为j条件下的最大价值
for (int i = 1; i <= n; i++)
    for (int j = w[i]; j <= m; j++)
        f[j] = max(f[j], f[j - w[i]] + v[i]); // max(不装物品i，装物品i(包含了装1个...装j/w[i]个的情况))  
cout << f[m];

注意： 内层循环遍历容量时，一定要是顺序的，因为我们在优化后的二维形式中写道，二维数组中计算f[i][j]时，就是需要使用到左侧（同一层）的计算结果，对于一维形式来说就是要使用已经计算后的结果。一维形式中，如果逆序遍历容量，计算后面容量时，使用的就是没有计算过的结果，体现在二维中，使用的就是上一层的结果，这是不对的

01背包和完全背包问题的一维写法只差了一个遍历的顺序，01背包使用逆序遍历，完全背包使用顺序遍历，因为转换到二维形式，01背包只需要使用的是上一层的结果，完全背包需要使用当前层的结果

三、多重背包问题

01背包：物品i最多选1次
完全背包：物品i可以选无数次
多重背包：物品i最多选 $s_i$ 次

由于多重背包和完全背包都是可以物品选多次，所以状态转移方程也一样，只是多了一个限制条件

朴素写法如下：

f[i][j] = max(f[i-1][j], f[i-1][j-k*w[i]]+k*v[i]) // k为 0 -> s[i]

// f[i][j]表示在考虑前i个物品后，背包容量为j条件下的最大价值
int f[N][M];    
for (int i = 1; i <= n; i++)
    for (int j = 1; j <= m; j++)
    	// 第三重循环遍历上述的椭圆，找最大值，分别表示物品i取几次
        for (int k = 0; k <= j / w[i] && k <= s[i]; k++)
            f[i][j] = max(f[i][j], f[i - 1][j - k * w[i]] + k * v[i]);   // 注意和01背包的对比
cout << f[n][m];

我们试试使用完全背包问题的优化方式

$f(i,j)=max(f(i−1,j),f(i−1,j−w_i)+v_i,f(i−1,j−2w_i)+2v_i,⋯,f(i−1,j−s_iw_i)+s_iv_i)\quad\quad\quad(1)$

上述max括号里总共s[i]+1项

考虑到：

$f(i,j−w_i)=max(f(i−1,j−w_i),f(i−1,j−2w_i)+v_i,f(i−1,j−3w_i)+2v_i,⋯,f(i−1,j−s_iw_i)+(s_i−1)v_i),\\\quad\quad\quad\quad\quad\quad\quad f(i−1,j−(s_i+1)w_i)+s_iv_i)\quad\quad\quad\quad\quad\quad\quad(2)$

max(放0个物品i，放1个物品i，放2个物品i，放s[i]个物品i)

上述max括号里总共s[i]+1项

上式变形得：

$f(i,j−w_i)+v_i=max(f(i−1,j−w_i)+v_i,f(i−1,j−2w_i)+2v_i,f(i−1,j−3w_i)+3v_i,⋯,f(i−1,j−s_iw_i)+s_iv_i,\\\quad\quad\quad\quad\quad\quad\quad\quad\quad f(i−1,j−(s_i+1)w_i)+(s_i+1)v_i))\quad\quad\quad(3)$

我们现在需要根据(3)式的结果，推出(1)式的结果，(1)式的后s[i]项和(3)式的前s[i]项完全一样，但我们无法使用(3)式中s[i]+1项的最大值，推出(3)式的前s[i]项的最大值，所以无法使用完全背包问题的优化方式

二进制优化

根据二进制表示，可以知道 $1,2,4,⋯,2^k$ 可以由系数0和1线性组合出 $0,2^k-1]$ ，如果我们用k+1个新的物品，来代替多重背包的一个物品，使用01背包的方式计算出这k+1个物品选或不选

比如说S=200，我们使用1、2、4、8、16、32、64、73这8个物品，代替200这个物品，对这8个物品进行选或不选，我们就能表示出当前这个物品选[0,200]次

按照上面的，如果给我们一个一般的S，我们使用1、2、4、8、…、 $2^k$ 、C，组合出S，则我们有 $1+2+4+8+...+2^k\leq s$ ，以及 $\\0\leq C<2^{k+1}$

也就是说，给我们一个物品最多选择S次，其实就是有S个这样的物品，我们可以将S个相同的物品，按照二进制的方式合并成 $log_2S+1$ 个物品，再对这 $log_2S+1$ 个物品使用01背包算法，如果说原来有n类物品，每类物品有s个，总共 $n s$ 个，我们合并后，就变成了总共 $n(log_2S+1)$ 个

// 读入物品个数时顺便打包
int k = 1;              // 当前包裹大小
int idx = 0;
// n表示原来物品数量，循环读入n个物品的重量，价值，数量
for(int i = 1; i <= n; i++){
	cin >> wi >> vi >> si;   // 物品重量，物品价值，物品数量
	// 开始用si个物品合成log2 si个物品
	while (k <= si){
	    idx++ ;              // 实际物品种数
	    w[idx] = wi * k;
	    v[idx] = vi * k;
	    si -= k;
	    k *= 2;             // 二进制倍增包裹大小
	}
	if(si > 0){
		idx++;
		w[idx] = wi * si;
		v[idx] = vi * si;
	}
}
//现在的n表示合成后的物品数量
int n = idx;
for(int i = 1; i <= n; i++){
	for(int j = m; j >= v[i]; j--){
		f[j] = max(f[j], f[j-w[i]]+v[i]);
	}
}
cout << f[m];

四、分组背包

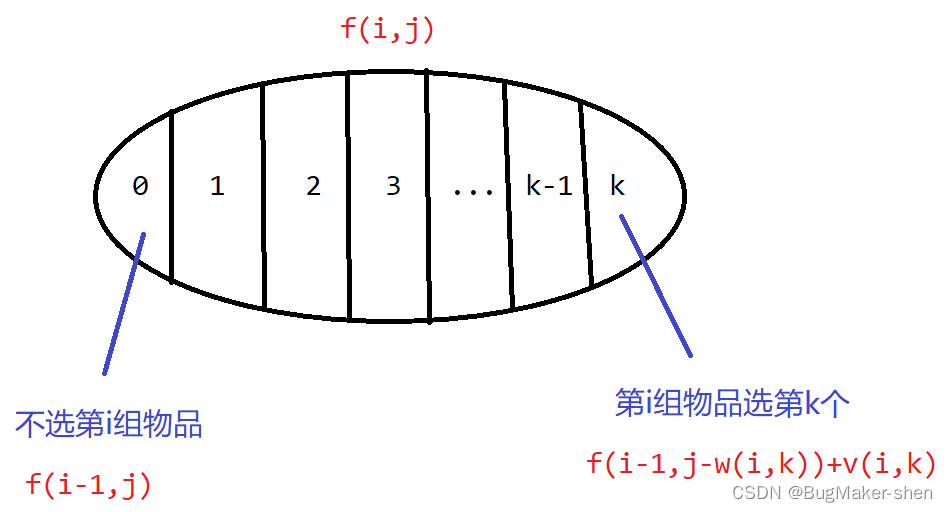
完全背包问题是考虑第i个物品选几个，分组背包问题是考虑第i组物品选哪个或不选（每组物品中至多拿1个）

实际上是带有约束的01背包问题，状态计算为： $f (i, j) = m a x (f (i - 1, j), f (i - 1, j - w (i, k)) + v (i, k))$

在这里插入图片描述

// n组物品
for(int i = 1; i <= n; i++){
	cin >> s[i];
	for(int j = 1; j <= s[i]; j++){
		cin >> w[i][j] >> v[i][j];
	}
}

// 遍历物品组数
for(int i = 1; i <= n; i++){
	// 遍历背包容量
	for (int j = m; j >= 1; j -- ){
		// 组内遍历物品
		for(int k = 0; k <= s[i]; k++){
			f[j] = max(f[j], f[j-w[i][k]]+v[i][k]);
		}
	}
}
cout << f[m] << endl;