1.什么是树
1.1树的概念
树(Tree)是n(n>0)个节点的有限集,n=0称为空树。
在任意一个棵非空树中:
1.有且仅有一个特定的称为根(Root)的结点;
2.当n>1时,其余节点可以分为m个(m>0)互不相交的T1,T2.....Tm其中每一个集合本身也是一课树并且称为根的子树(SubTree)
注:
在一棵完整的树中,根节点时唯一的;
子树的个数是不限的但是也是互不相交的
1.2 节点度
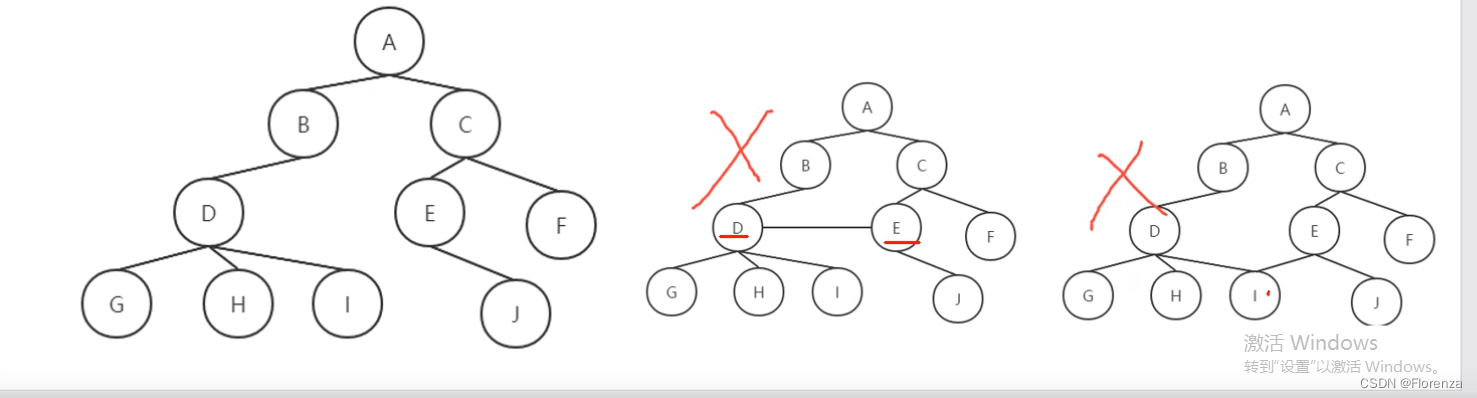
节点度(Degree)算法为每个节点计算与其相连的边的数量;当边上有权重时,则计算权重的总和。节点度是面向节点的浅层(≤ 1层)计算,是一种最简单、最高效的图算法,在科学计算、特征提取、超级节点识别等领域扮演着至关重要的角色。
A的度为2
B的度为1
C的度为2
D的度为3
...

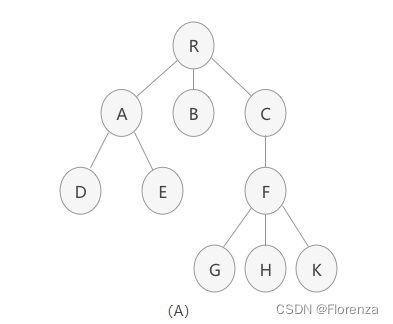
1.3 树的度
树的度指的是结点拥有的子树称为子树的度。一棵树中,最大的节点的度称为树的度。树由根结点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点,所定义的关系称为父子关系
上面树的度就是3
2.树的表示
2.1双亲表示法
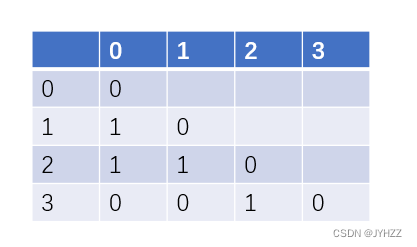
我们假设以一段连续空间存储树的结点,同时在每个结点中,附设一个指示器指示其双亲结点到链表中的位置。也就是说,每个结点除了直到自己是谁外,还要直到自己的双亲在哪里。如图
通过一个编号来指明节点,再通过一个字段来指明节点的父级
有了这样的结构定义,我们就可以实现双亲定义法了。由于跟结点没有双亲,所以我们约定根结点的位置域设置为-1,这就意味着,我们所有结点都直到他双亲的位置。如图的树结构和双亲表示法的图表。
我们可以通过上面快速的找到结点的双亲。
存在问题:
但是我们要知道结点的孩子怎么办?那就只有遍历整个结构了。
2.2孩子表示法
2.2.1 孩子表示法一:每一个节点有一个域,域等于树的度
指针域的个数等于树的度。(树的度是树各个结点度的最大值)。(结点拥有的子树称为结点的度)。
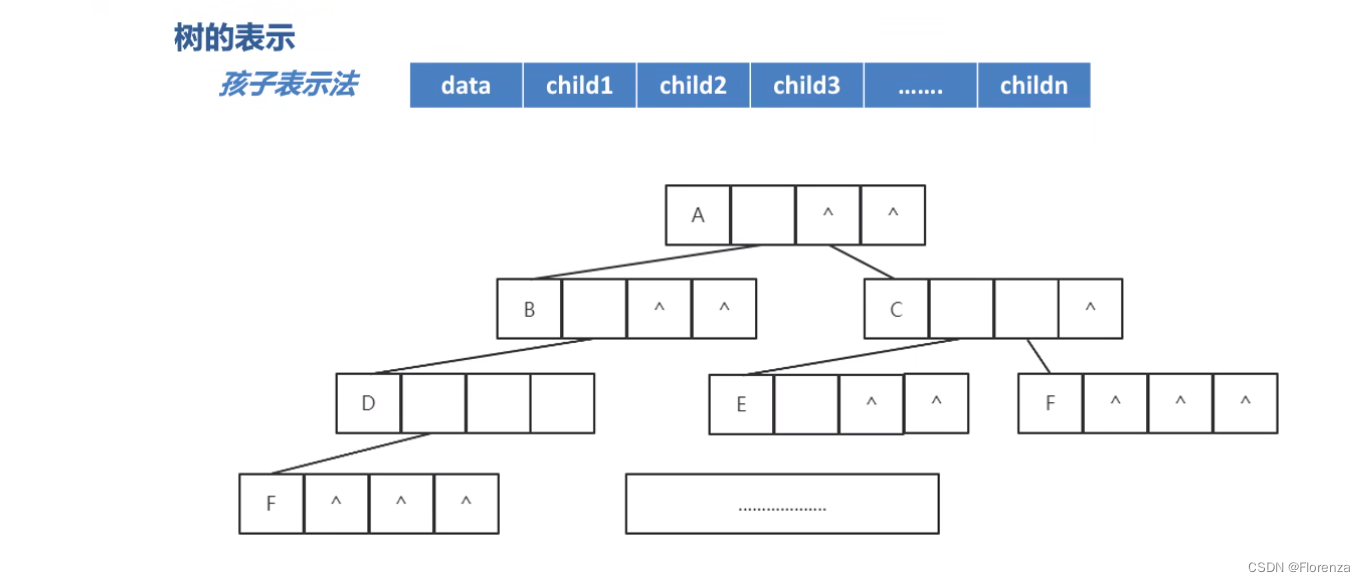
存在问题:
空间浪费
^这个符号就是代表当前这个指针域并没有用到。这样如果树的各结点的度差距过大的话,显然非常浪费空间。那我们为什么不按需分配空间呢?这样就有第二种方案了
2.2.2 孩子表示法二:
每个结点指针域的个数等于该结点的度,我们专门来取一个位置来存储结点指针域的个数。如图
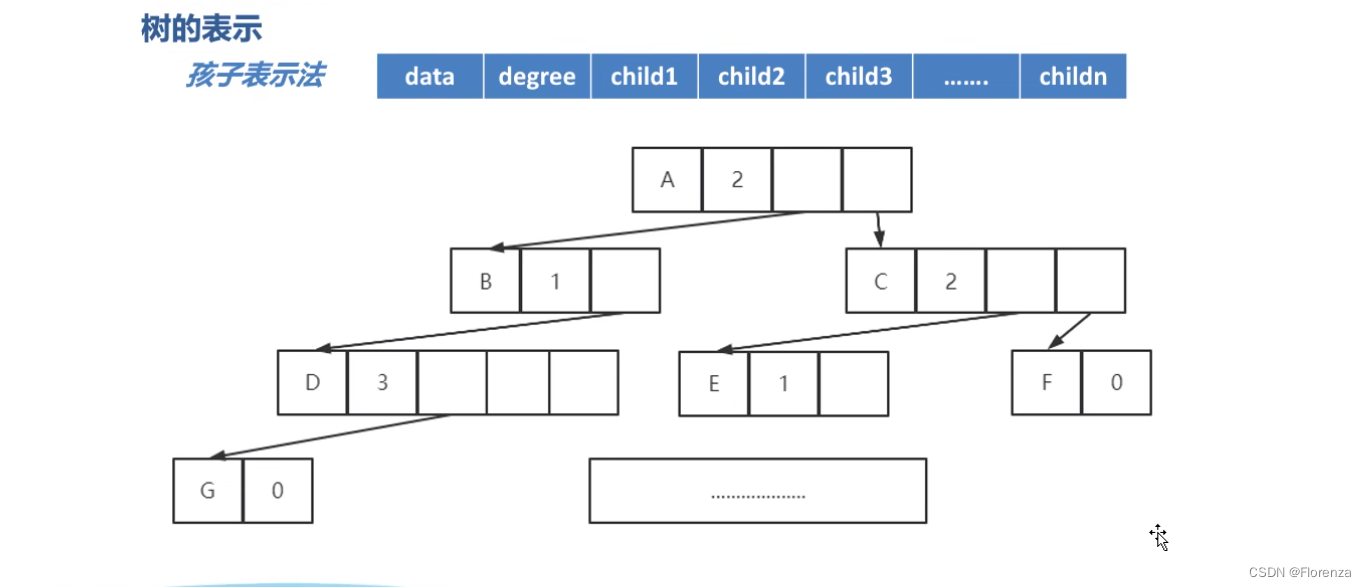
显然,方案二克服了浪费空间的缺点,
存在问题:
由于各个结点的链表结构是不相同的,在加上要维护结点的度的数值,在运算上显然有损耗。
能否有更好的方法?既可以减少浪费,又能使结点结构相同。
我们把每一个结点放入顺序存储结构中是合理的,但是每个结点的孩子多少是不确定的,所以我们再对每个结点的孩子建立一个单链表来体现他们的关系。
这就是我们的孩子表示法。
具体办法:把每个结点的孩子排列起来,以单链表作存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空。然后n个头指针有组成一个线性表,采用顺序存储结构,存进一个一维数组。如图 所示
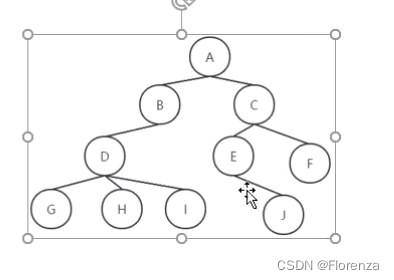
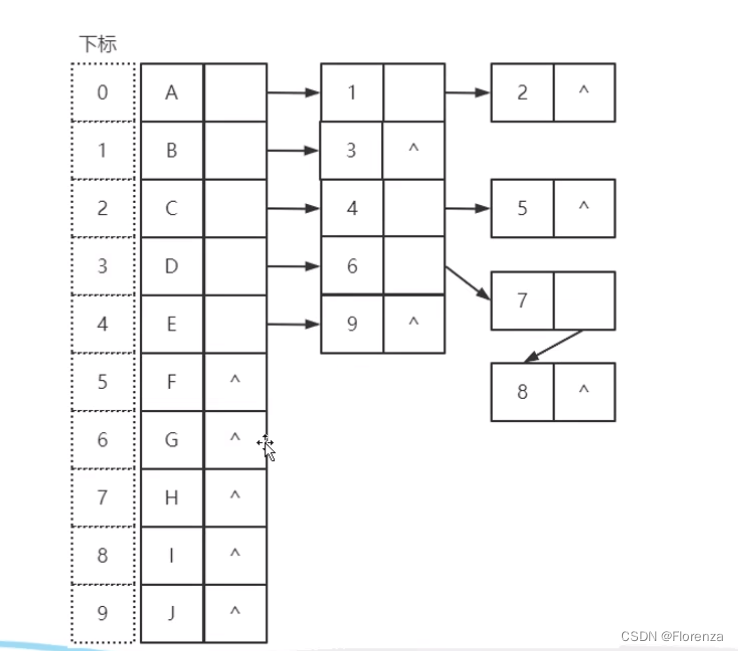
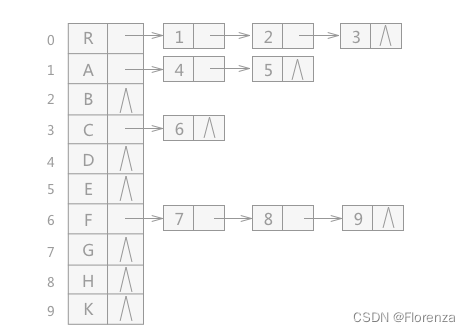
存在问题:
不好去找双亲节点
2.2.3 孩子表示法二:
我们可以改进一下。把双亲表示法和孩子表示法综合一下,加一个双亲域。如图。(双亲孩子表示法)
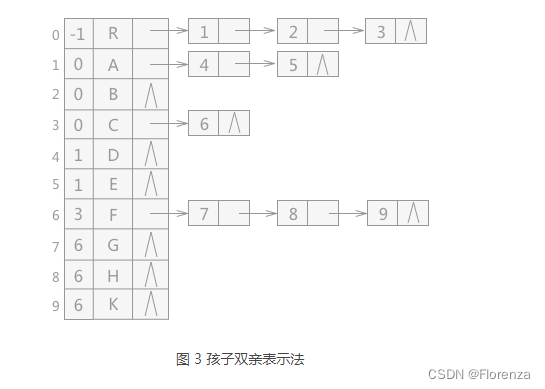
2.3 二叉树
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分 。
二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个节点 。
特殊类型:
1、满二叉树:如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树 。
2、完全二叉树:深度为k,有n个节点的二叉树当且仅当其每一个节点都与深度为k的满二叉树中编号从1到n的节点一一对应时,称为完全二叉树 。
二叉树 从左到右 一次编号与满二叉树对应编号一样则称为完全二叉树
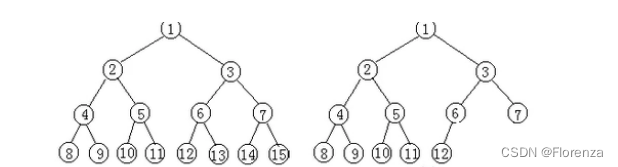
上图中 一一对应 所以就是一个完全二叉树
完全二叉树的特点是叶子节点只可能出现在层序最大的两层上,并且某个节点的左分支下子孙的最大层序与右分支下子孙的最大层序相等或大1。
推论
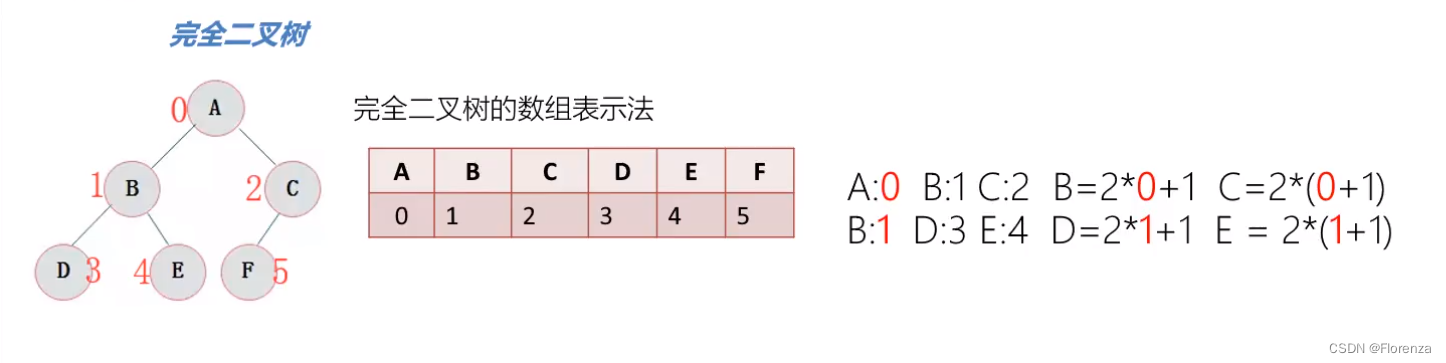
推论1:
对于位置为K(K为父节点序号)的节点,左子节点=2*K+1 右子节点=2K+2
验证: C=2*A+2 F=2*C+1
推论2:
最后一个非叶子节点的序号为 (N/2)-1 N为数组存储二叉树的 length
验证: 6/2-1=2 -------> C