1.一棵有124个结点的完全二叉树,其叶结点个数是确定的。T
什么是完全二叉树?(会的可以跳过)
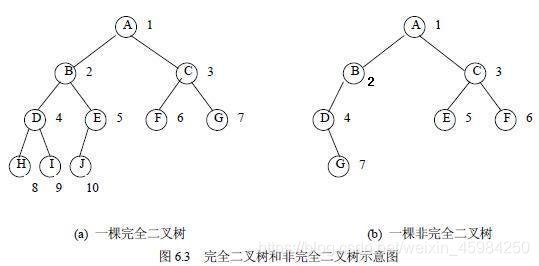
完全二叉树:一棵深度为k的有n个结点的二叉树,对其结点按从上至下,从左至右的顺序进行编号,如果编号为i的结点与满二叉树中编号为i的结点在二叉树的位置相同,则这棵二叉树为完全二叉树。
因为一棵非空二叉树的第i层上最多有 2的(i-1)次方个结点,所以可以推广到完全二叉树
性质1:一棵完全二叉树的第i层上最多有 2的(i-1) 次方个结点
因为一棵深度为k的二叉树中,最多有 2的k次方-1 个结点,也可以推广到完全二叉树
性质2:一棵深度为k的完全二叉树中,最多有 2的k次方-1 个结点
性质3:具有n个结点的完全二叉树的深度k为 log₂n向下取整,再+ 1。
例:有5个结点,log₂n向下取整为2,再+1为3。
由性质3可得,log₂124 向下取整 =6,再+1为7。
所以该二叉树的深度为7。
由性质2可得,深度为6的完全二叉树有2的6次方-1个结点,即63个结点。
总共有124个结点,那么还剩下124-63=61个结点,分布在第7层。
由性质1可得,第7层最多有2的(i-1)次方个结点,也就是2的6次方,最多64个,可以容纳下61个结点。
下面计算叶结点,第7层的结点全是叶节点,有61个,剩下的叶节点在第6层。
第7层的每2个结点是第6层的1个结点的左右孩子,因为61是奇数,所以最后还剩下一个结点对应第6层的一个结点。
(61-1)/2=30,即第6层有30个结点有左右孩子,有1个结点有1个孩子,第六层有2的5次方个结点,也就是32个,那么第6层没有孩子的结点有32-30-1=1个,这个结点是叶节点之一。
所以该完全二叉树共有61+1=62个叶节点
2.二叉树中序线索化后,不存在空指针域。 F
(无特殊说明的话,是没有头结点的,如果有头结点的话,为T)
第一个结点无前驱,最后一个结点无后继。
构造一个二叉树就偷点懒,用这个的结果(这叫复习/doge):
4-14 还原二叉树&&4-15 根据后序和中序遍历输出先序遍历
生成的树:
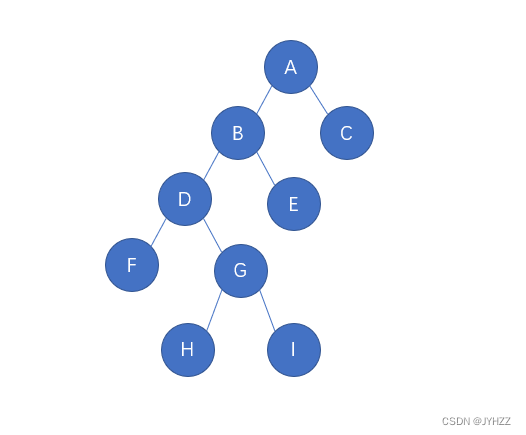
咱们就中序线索化这个。
代码:(有头结点的中序线索二叉树,不存在空指针域)
#include<iostream>
using namespace std;
typedef struct Tnode* Tree;
typedef struct Tnode{
char data;
Tree lchild;
Tree rchild;
unsigned ltag;
unsigned rtag;
};
Tree get(char s1[], char s2[], int n) {
if (n <= 0) {
return NULL;
}
Tree tree = (Tree)malloc(sizeof(struct Tnode));
tree->lchild = NULL;
tree->rchild = NULL;
tree->ltag = 0;
tree->rtag = 0;
tree->data = s1[0];
int i;
for (i = 0; s2[i] != s1[0]; i++);
tree->lchild = get(s1+1, s2, i);
tree->rchild = get(s1 + i + 1, s2 + i + 1, n - i - 1);
return tree;
}
int len(Tree tree) {
if (tree == NULL) {
return 0;
}
int left = len(tree->lchild);
int right = len(tree->rchild);
return (left >= right ? left : right) + 1;
}
Tree pre;
void InTreading(Tree tree) {
if (tree) {
InTreading(tree->lchild);
if (tree->lchild == NULL) {
tree->ltag = 1;
tree->lchild = pre;
}
if (pre->rchild == NULL) {
pre->rtag = 1;
pre->rchild = tree;
}
pre = tree;
InTreading(tree->rchild);
}
}
Tree InOrderThr(Tree tree) {
Tree head = (Tree)malloc(sizeof(struct Tnode));
head->lchild = 0;
head->rtag = 1;
head->rchild = head;
if (!tree) {
head->lchild = head;
}
else {
head->lchild = tree;
pre = head;
InTreading(tree);
pre->rchild = head;
pre->rtag = 1;
head->rchild = pre;
}
return head;
}
Tree InpostNode(Tree p) {
Tree post;
post = p->rchild;
if (p->rtag != 1) {
while (post->ltag == 0) {
post = post->lchild;
}
}
return post;
}
void Search(Tree tree) {
Tree temp;
temp = tree->lchild;
while (temp->ltag == 0 && temp != tree) {
temp = temp->lchild;
}
while(temp!=tree){
printf("%c ", temp->data);
temp = InpostNode(temp);
}
}
int main()
{
int n;
cin >> n;
char s1[51], s2[51];
for (int i = 0; i < n; i++) {
cin >> s1[i];
}
for (int i = 0; i < n; i++) {
cin >> s2[i];
}
Tree st= get(s1, s2, n);
st = InOrderThr(st);
Search(st);
return 0;
}3.对N(≥2)个权值均不相同的字符构造哈夫曼树,则树中任一非叶结点的权值一定不小于下一层任一结点的权值。T
解析:考察哈弗曼树的构造方法,哈弗曼树的构造思想就是贪心的思想,每次选择权值最小的两个节点来形成新的节点,自底向上建树,因此对于一棵哈弗曼树来说,树中任一非叶节点的权值一定不小于下一层的任意节点的权值。
在构造哈夫曼树时会遇到两种情况,一种是造成树的高度增加,一种是不增加:
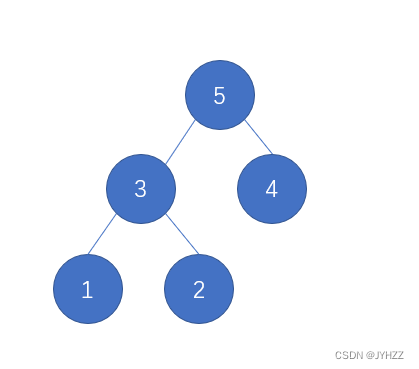
高度增加的情况:1,2,3,4。即每向树增加结点,树高加一
高度不增加的情况:比如6,7,8,9。在增加8和9时,树高不会立刻增加(就当成是树吧)
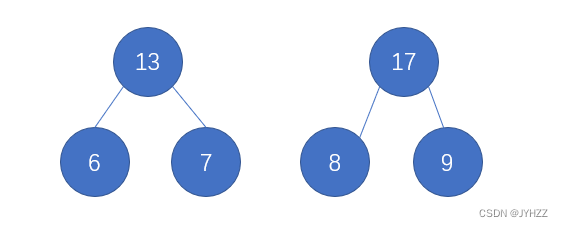
无论是这两种那种情况,都满足题意
4.哈夫曼编码是一种最优的前缀码。对一个给定的字符集及其字符频率,其哈夫曼编码不一定是唯一的,但是每个字符的哈夫曼码的长度一定是唯一的。T
哈夫曼编码一般左0右1
比如这个哈夫曼树:
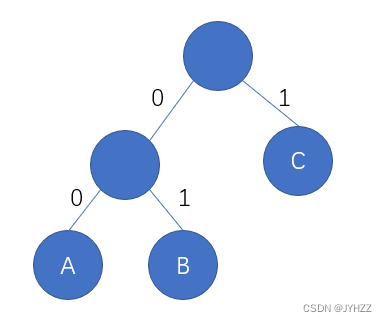
哈夫曼编码:
A:00
B:01
C:1
我们在构造时也可能会这样:
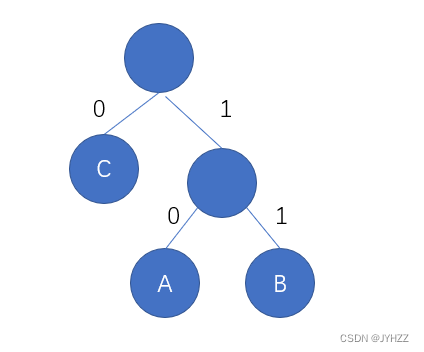
这样构造也是对的,但是哈夫曼编码就不一样了:
哈夫曼编码:
A:10
B:11
C:0
所以,对一个给定的字符集及其字符频率,哈夫曼编码不一定是唯一的。
因为无论怎么构造,对一个给定的字符集及其字符频率,不同的哈夫曼树的“样子”只是交换左右子树造成的,所以每个字符的哈夫曼码的长度一定是唯一的。(哈夫曼码的长度即该字符所在叶节点的树的分叉的高)
5.对于一个有N个结点、K条边的森林,不能确定它共有几棵树。F
对于一棵树,有这样的性质:节点数-边数=1。
例如:
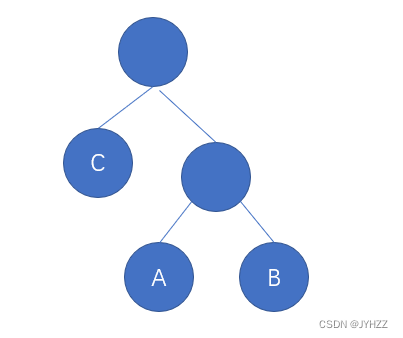
有5个结点,4条边
森林是0棵或有限棵不相交的树的集合,比如森林中有3棵树,那么每棵树的结点数比边数多1,那么三棵树的总结点数就比总边数多3。由此可得,对于一个有N个结点、K条边的森林,它有N-K棵树
6.树的后根序遍历序列等同于它所对应二叉树的中序遍历序列。T
树的先序遍历与其转换成二叉树的先序遍历的结果相同;
树的后序遍历与其转换成二叉树的中序遍历的结果相同;
7.二叉树可以用二叉链表存储,树无法用二叉链表存储。F
一个结点的第一个孩子(长子)作为该节点的左孩子,这个结点的兄弟这个结点作为右孩子。
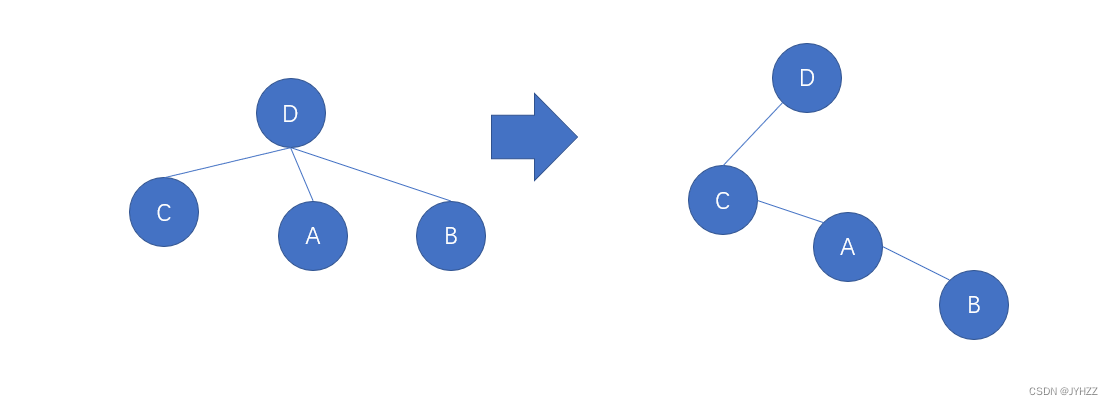
8.将一棵树转成二叉树,根结点没有左子树。F
根节点没有兄弟,所以根节点没有右子树
9.用邻接矩阵法存储图,占用的存储空间数只与图中结点个数有关,而与边数无关。T
占用的存储空间数只与图中结点个数有关,而与边数无关,空间代价为O(n*n);
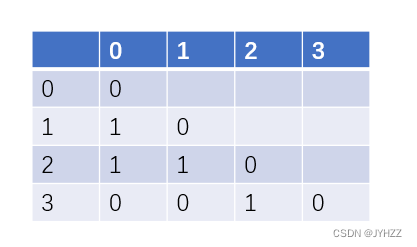
10.用一维数组G[]存储有4个顶点的无向图如下:
G[] = { 0, 1, 0, 1, 1, 0, 0, 0, 1, 0 }
则顶点2和顶点0之间是有边的。T
下三角矩阵