目录
Gauss算法
Strassen算法
Winograd算法
Winograd 1D
Winograd 2D
在硬件设计中,乘法无论是在逻辑资源的使用上还是组合逻辑的延时上都要比加法高很多。从硬件方面考虑,我们都更倾向于将乘法转换成移位和加法,譬如乘以8,可以转换为左移3位。A*15可以转换为(A<<4) - A,将乘法转换为其他的运算以减少资源消耗和组合逻辑延时。
但有时候乘以的数值不是定值的时候,我们在硬件上就很难将乘法转化为移位和加法,那么在乘法无法避免的时候,如何减少乘法的次数就显得至关重要。
Gauss算法
Gauss算法优化乘法
计算(a+bi)*(c+di) 时,总共涉及到的乘法次数为四次乘法和三次加法。
使用gauss算法优化:
经过Gauss算法优化之后,实部为,虚部为
。整个计算量从原来的4次乘法+3次加法,变到了3次乘法+5次加法,减少了乘法次数。
Strassen算法

上面的矩阵乘法,总共用到了8次乘法+4次加法。
Strassen算法和Gauss算法很相似,优化的方法如下:
Strassen算法应用在2X2的矩阵乘法可以将8次乘法+4次加法,转换为7次乘法 + 18次加法。
如果矩阵B是常数,譬如权重矩阵。那么Strassen算法可以将8次乘法+4次加法,转换为7次乘法 + 13次加法,减少了乘法次数。
Strassen算法通过减少乘法数,把矩阵乘法的复杂度从 Θ(N3) 减少到 Θ(N2.807),减少了计算次数的代价就是需要更多的内存。
Winograd算法
Winograd是一种计算短卷积的快速算法。
一维卷积运算定义为F(m,r),m为Output Size,r为Filter Size,则输入信号的长度为m+r−1: 
卷积运算是对应位置相乘然后求和,输入信号每个位置至少要参与1次乘法,所以乘法数量最少与输入信号长度相同,记为:
在行列上分别进行一维卷积运算,可得到二维卷积,记为F(m×n,r×s),输出为m×n,卷积核为r×s,则输入信号为(m+r−1)(n+s−1),乘法数量至少为μ(F(m×n,r×s))=μ(F(m,r))μ(F(n,s))=(m+r−1)(n+s−1)。
Winograd 1D
输入信号为,卷积核为
,输入为1*4矩阵,卷积核为1*3矩阵,两者卷积结果会得到两个值,可以把上述卷积过程写为如下矩阵乘法形式
如果是一般的矩阵乘法,则需要进行6次乘法和4次加法,过程如下:
WInograd 算法是面向卷积的运算而不是普通的矩阵相乘:
其中:
Winograd的计算需要进行4次乘法+12次加法+2次移位。如果卷积核filter的为常数,例如filter为固定权重矩阵,则Winograd的计算需要进行4次乘法+8次加法。
为了方便,Winograd 1D可以表示为:
其中为点积,即对位相乘。
为Input transform矩阵,尺寸为
,G为Filter transform矩阵,尺寸为
r,
为output transform矩阵,尺寸为
:
g卷积核:; d输入信号:
,将这些矩阵带入到Y等式中,就能推出和上面F(2,3)一样的结果。
Winograd 2D
根据Winograd 1D公式,可以如下化简:
对于二维卷积,如右图所示,用一个3*3的卷积核对4*4的区域进行卷积,总共会卷积四次,我们将3*3的卷积核拉长成一个9*1的矩阵,4*4的区域按照和卷积核的乘法方式,扩展为一个4*9的矩阵,这样这个4*9的区域扩展矩阵和9*1的卷积核扩展矩阵的乘积还是等于卷积结果:
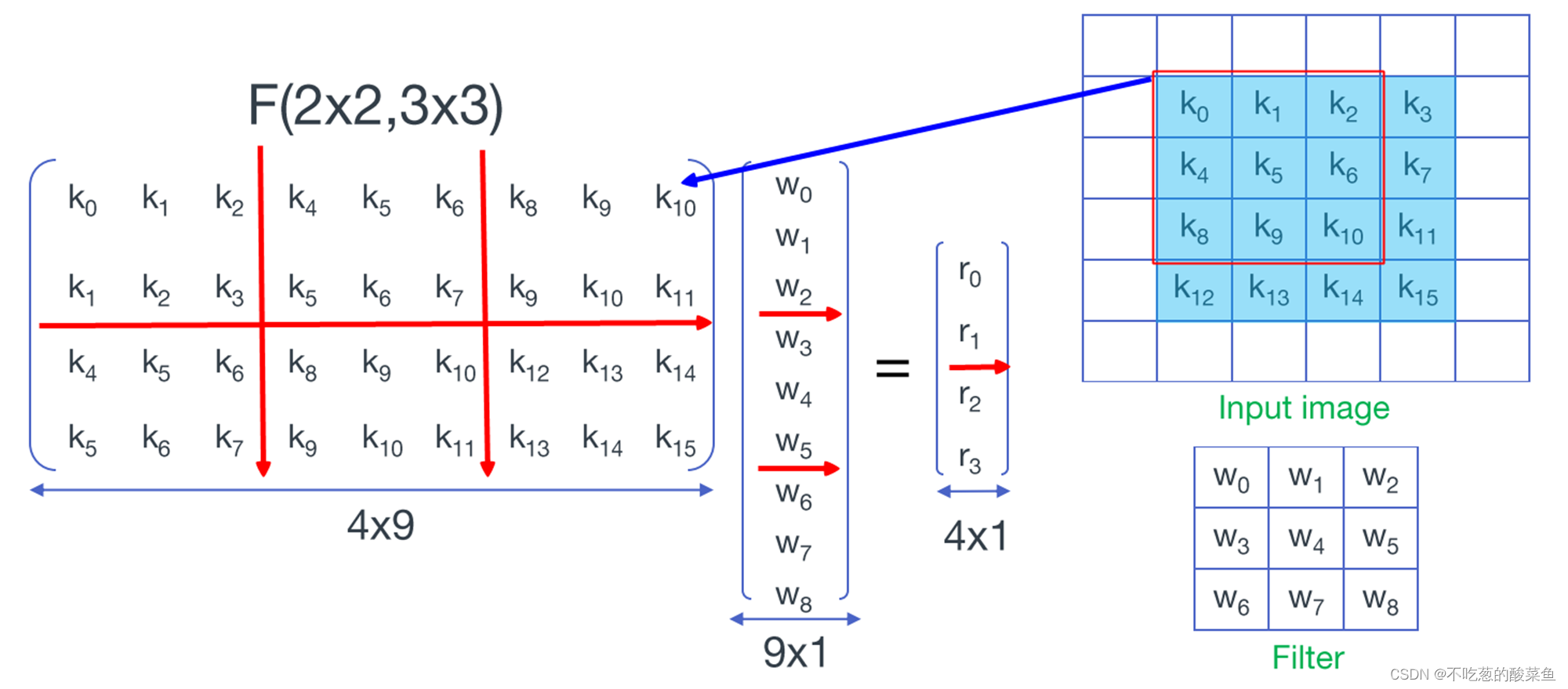
通过上面这种方式优化,我们就成功的将2D的卷积,转化为了1D的乘法,就可以使用我们前面Winograd 1D的化简公式来优化卷积乘法。
每个子矩阵中重复元素的位置与一维时相同,同时重复的子矩阵也和一维时相同

我们就可以把Winograd 1D的乘法模块复用到2D中:
令,即窗口中的第0行元素,
表示第1、2、3行;
,因此我们可以推导出如下结果:

简单来说,1D Winograd被嵌套成了2D Winograd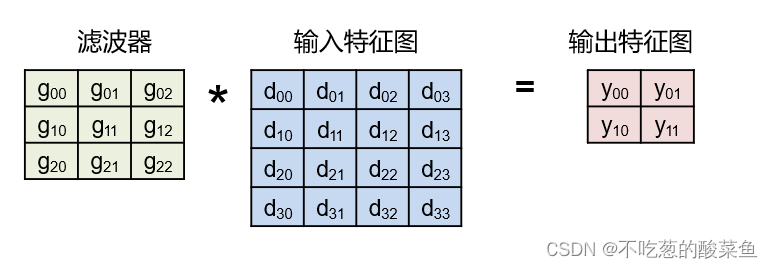
对于如上的乘法,直接卷积将会进行36次乘法(4*9),采用Winograd算法,可以将乘法的数目减少到16次,减少了2.25倍,对优化卷积算法效果显著。