前言

前面我们介绍了指数函数及其基本性质以及如何在笛卡尔直角坐标系下绘制静态的指数函数图像，这一节，我们将重点讨论一下指数函数的导函数以及导函数的动态表示，为方便起见，以下列指数函数为例

$$f(x)=e^x$$

指数函数的导函数

下面我们先来推导一下指数函数的导函数，根据导函数的定义式

$$\begin{array}{rl}(e^x{)}^{\prime }& =\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x)-f(x)}{\Delta x}\\ & =\underset{\Delta x\to 0}{\lim }\frac{e^{x+\Delta x}-e^x}{\Delta x}\\ & =\underset{\Delta x\to 0}{\lim }\frac{e^x(e^{\Delta x}-1)}{\Delta x}\end{array}$$
令 $e^{\Delta x}-1=y$， 则 $\Delta x=ln(y+1)$，代入上式有

$$\begin{array}{rl}(e^x{)}^{\prime }& =\underset{\Delta x\to 0}{\lim }\frac{e^x(e^{\Delta x}-1)}{\Delta x}\\ & =e^x\underset{y\to 0}{\lim }\frac{y}{ln(y+1)}\\ & =e^x\underset{y\to 0}{\lim }\frac{1}{\frac{1}{y}ln(y+1)}\\ & =e^x\underset{y\to 0}{\lim }\frac{1}{ln(y+1{)}^{\frac{1}{y}}}\\ & =e^x\end{array}$$

非常有趣的是，指数函数$e^x$的导函数表达式与其原函数一样，这也就是说导函数和原函数在同一位置的取值相等，下面我们可以通过动图能够非常清晰的看到这一个性质。

指数函数导函数动图绘制

因为导函数的定义是根据极限来定义的，为此，我们通过控制自变量的增量$\Delta x$，让其足够的小，最好近似趋向于0，导函数的取值就是近似该点的切线斜率，依循这个思路可以模拟出指数函数各点的切线，通过切线的移动来对比指数函数的值和切线斜率的取值。

# -*- coding: utf-8 -*-
"""
Created on Sun Feb 16 10:19:23 2020
project name:
@author: 帅帅de三叔
"""
import math
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

#初始化画布
fig = plt.figure()
plt.grid(True)

#绘制一条正弦函数曲线
x = np.linspace(0, 7,100)
y = np.exp(x)
curve_ani, = plt.plot(x, y, color = 'red', alpha=0.8, label = '$y=e^x$') #指数函数曲线
point_ani, = plt.plot(0,0, color = 'red',alpha=0.5, marker='o') #切点


xtext_ani = plt.text(5.5,50,'',fontsize=12)#自变量
ytext_ani = plt.text(5.5,130,'',fontsize=12)#因变量
ktext_ani = plt.text(5.5,200,'',fontsize=12)#斜率

delta = 0.05 #用来控制精度

def gradient(x0): #x0处的切线斜率
    num_min = np.exp(x0 - delta)
    num_max = np.exp(x0 + delta)
    k = (num_max - num_min) / (2*delta)
    return k

def tangent_line(x0,y0,k): #过x0,y0的切线段
    xs = np.linspace(x0 - 0.5,x0 + 0.5,100)
    ys = y0 + k * (xs - x0) #切线方程
    return xs,ys

k = gradient(x[0])
xs,ys = tangent_line(x[0],y[0],k)

tangent_ani,  = plt.plot(xs,ys,c='blue',alpha=0.8)


def update(num):
    k=gradient(x[num])
    xs,ys = tangent_line(x[num],y[num],k)
    tangent_ani.set_data(xs,ys)
    point_ani.set_data(x[num],y[num])
    xtext_ani.set_text('x=%.3f'%x[num])
    ytext_ani.set_text('y =%.3f'%y[num])
    ktext_ani.set_text('y\'=%.3f'%k)
    return [point_ani,xtext_ani,ytext_ani,tangent_ani,k]

ani = animation.FuncAnimation(fig=fig,func=update,frames=np.arange(0,100),interval=200)

ani.save('D:\exponential.gif')
plt.legend()
plt.show()

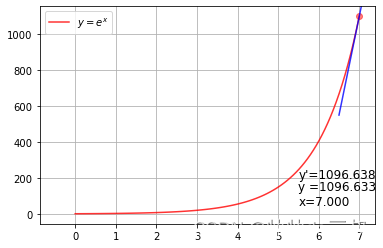
效果预览

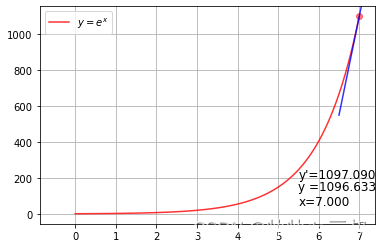
从效果预览，我们可以看到随着切点横坐标的不断增大，切线段的长度也在不断变长，指数函数取值y与其导函数取值y’取值很靠近，最后定格在x=7，此时因变量取值是1096.633，切线斜率为1097.090。

由导函数的推导可以看出，有兴趣的读者可以自行控制$\Delta$大小来观察原函数取值与导函数取值的大小放缩关系，如下就是Delta取值0.005的效果，很明显y与y’的差距更小了，我们知道随着delta趋向于0，二者的值将相等，这也符合我们的预期。

参考文献

1，https://blog.csdn.net/zengbowengood/article/details/104260155
2，https://blog.csdn.net/zengbowengood/article/details/104338878
2，https://blog.csdn.net/weixin_43628432/article/details/105879254