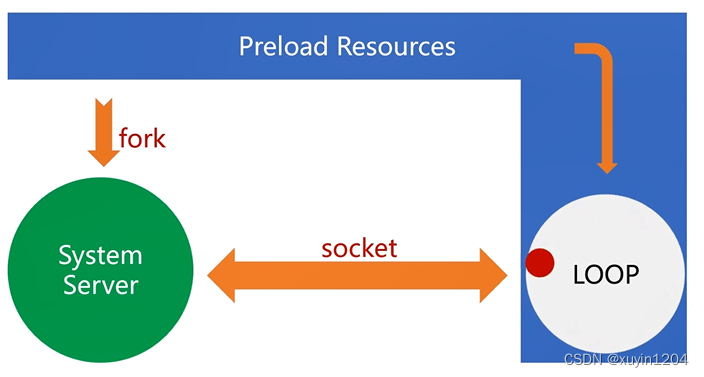
题目描述

一个正整数如果能被 a 或 b 整除，那么它是神奇的。
给定三个整数 n , a , b ，返回第 n 个神奇的数字。因为答案可能很大，所以返回答案 对 109 + 7 取模 后的值。

示例 1：

输入：n = 1, a = 2, b = 3
输出：2

示例 2：

输入：n = 4, a = 2, b = 3
输出：6

提示：

1 <= n <= 10⁹
2 <= a, b <= 4 * 10⁴

方法一：二分查找+容斥原理

class Solution {
public:
    const int MOD = 1e9 + 7;
    int nthMagicalNumber(int n, int a, int b) {
        long lcm = std::lcm(a, b); // 计算a和b的最小公倍数
        // 二分上界为a，b中较小值的 n 倍
        // 此时能够保证最少有 n 个神奇数字
        long left = 0, right = (long) min(a,b) * n; // 开区间
        while(left + 1 < right){
            long mid = (left + right) / 2;
            if(mid / a - mid / lcm + mid / b < n){
	            // 增大下界 left = mid
                left = mid;
            }
            else{
                // 减小上界
                right = mid;
            }
        }
        return right % MOD;
    }
};

心得

• 今天时间比较赶，看了困难就没打算自己敲了，不过看到题目提示了暴力求解可能会出现TLE，有想到前几天一道题目，[ 891.子序列宽度之和 ]，果然， 这道题也是要用二分查找的方法，今天听了灵神的视频把二分查找学会了，希望下次可以自己敲出来。

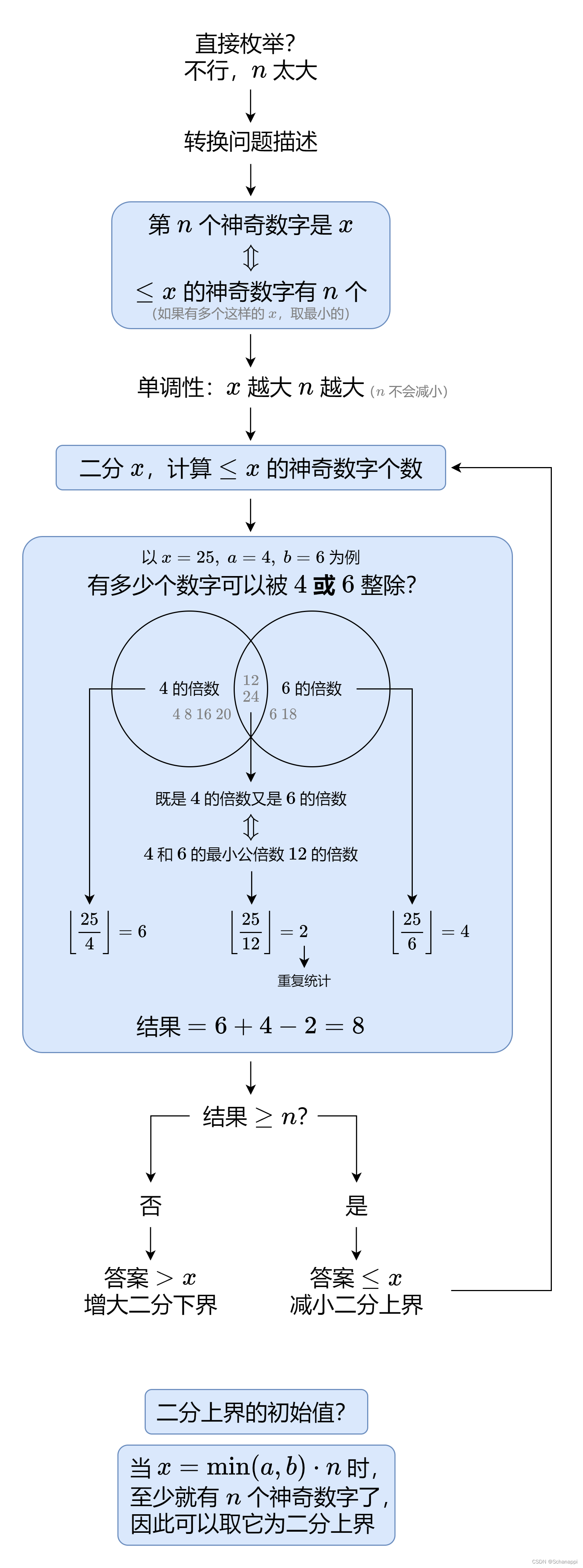
• 方法：二分查找+容斥原理
  具体思路看下面的图解，很清晰了。
  主要讲一下需要注意的几个点：

  • 求解最小公倍数有函数lcm，不过使用的时候记得要std::lcm()，前面的std不可以缺少；
  • 以后遇到数字很大的情况，记得要灵活使用long的数字类型；

• 解释一下：为什么二分循环结束时，得到的一定是一个神奇数字？
  答：设答案为 x，循环结束时，≤ x 的神奇数字有 n 个，而 ≤x−1 的神奇数字不足 n 个（可结合视频中的红蓝染色来理解）。只有当 x 是一个神奇数字时，才会出现这种情况。
  这也同时说明，在二分循环中，我们不能在计算结果恰好等于 n 的时候，直接返回答案，而是要继续二分。