推翻了自己的三次理论，最终确定informer流程。自己梳理，有错请提示，以便及时改正
一、流程图

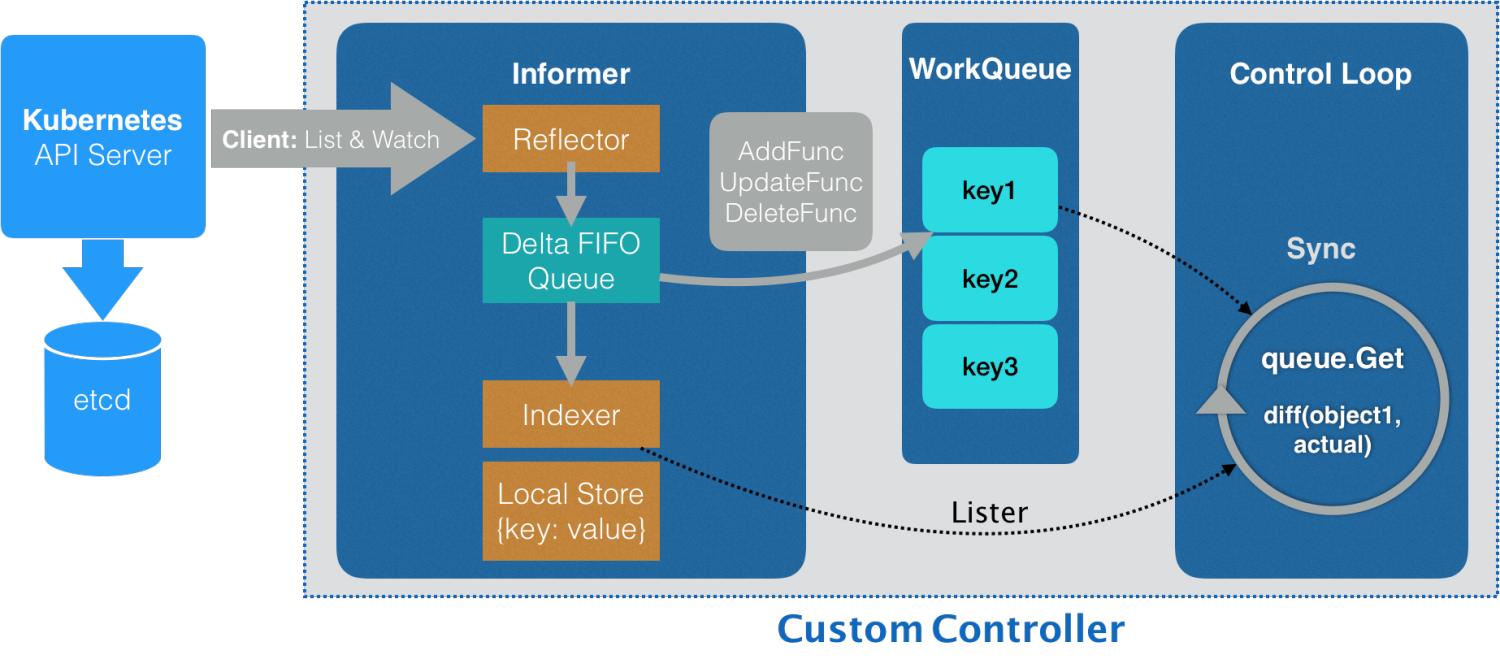
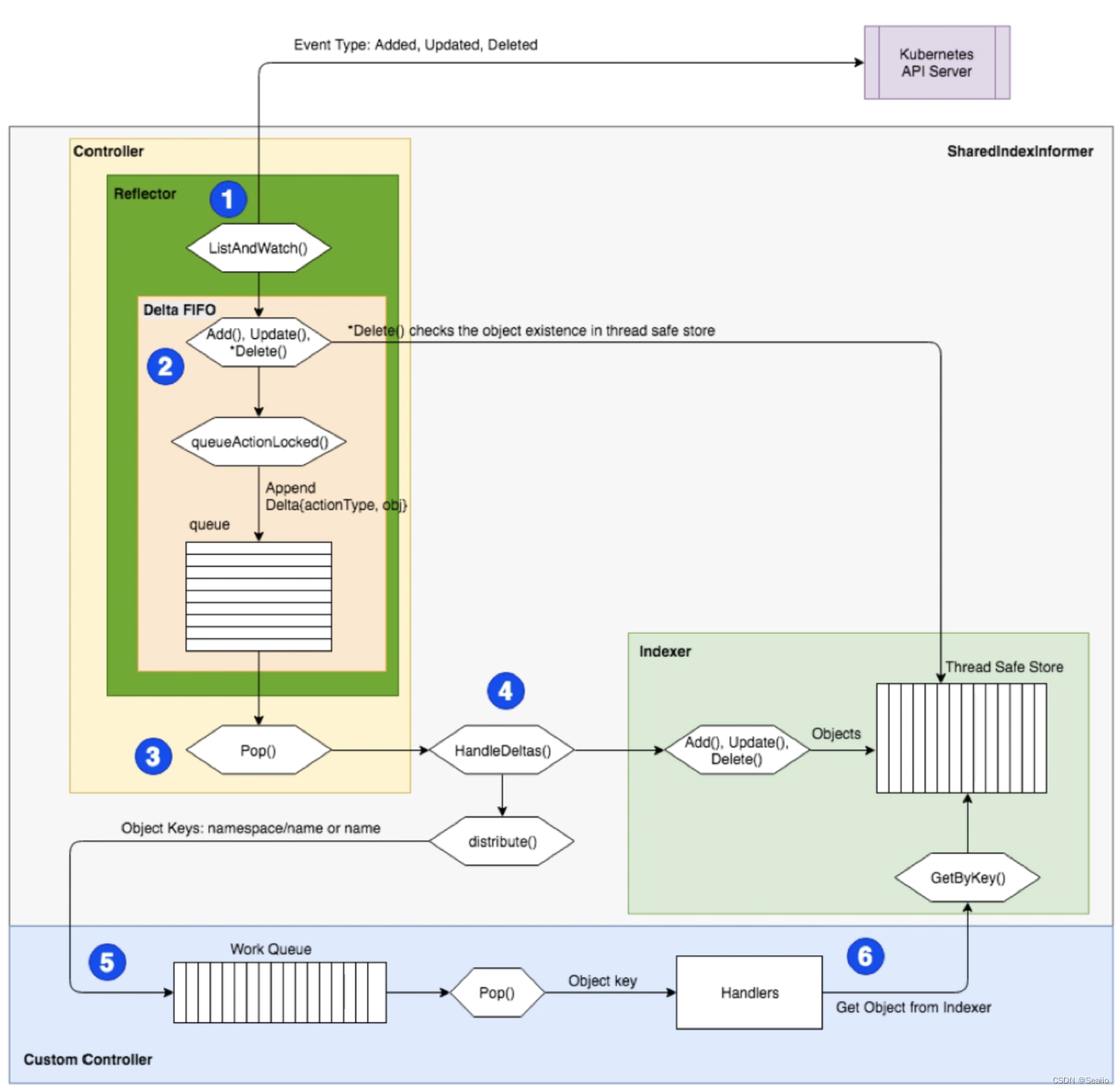
图1为整体流程，图2位细节流程
二、主要组件

1. Reflector-负责与API-Server进行绑定
2. Delta FIFO-增量先进先出队列
3. Indexer-本地缓存
4. ResourceEventHandler-可以注册EventHandler的client（用于回调）
5. Work Queue-工作队列，负责用户处理
6. Handler-用户的Handler，负责处理真正的业务逻辑

三、步骤解析

1. informer分两步，一步为k8s内部处理，一步为Custom用户自行处理
2. Reflector负责ListAndWatch与api-server连通。List短连接一次性获取所有最新版本的API对象，WATCH长链接“监听”API对象的变化
3. 获取到的数据推入Delta FIFO队列中，并同时更新Indexer本地缓存数据（key=>val格式）
4. 从Delta FIFO中pop一个数据，触发EventHandler回调，将key推送到Work Queue队列
5. 从Work Queue中pop一个key，然后根据key去Indexer取到val。根据当前的EventHandler（增、删、更新）进行创建pod操作。
   四、细节分析
6. 第3步和第4步，用了两个队列的原因，为了监听获取到的数据和用户处理数据时间不一致。导致用户时间处理过长，进而阻塞住Delta FIFO。导致崩死。分成两个队列处理解耦，”消费者“/”生产者“进行区分
7. resync机制，该机制是通过定时从API-Server读取最新数据更新到本地缓存indexer中，确保本地缓存的一致性。该机制会触发EventHandler的update操作。会重新讲key推入到Delta FIFO中，逐步到达Work Queue后，通过判断新的（LIST过来的）和老的（曾经indexer中的）数据的版本号进行比对，如果相同则跳过，否则更新。该机制是为了确保Custom Controller在最后一步创建pod时失败。