纪念本狗第三次AK！！！

2469. 温度转换

给你一个四舍五入到两位小数的非负浮点数 celsius 来表示温度，以 摄氏度（Celsius）为单位。

你需要将摄氏度转换为 开氏度（Kelvin）和 华氏度（Fahrenheit），并以数组 ans = [kelvin, fahrenheit] 的形式返回结果。

返回数组 ans 。与实际答案误差不超过 $10^{-5}$ 的会视为正确答案。

注意：

• 开氏度 = 摄氏度 + 273.15
• 华氏度 = 摄氏度 * 1.80 + 32.00

提示：

• 0 <= celsius <= 1000

示例

输入：celsius = 36.50
输出：[309.65000,97.70000]
解释：36.50 摄氏度：转换为开氏度是 309.65 ，转换为华氏度是 97.70 。

思路

简单模拟

// C++
class Solution {
public:
    vector<double> convertTemperature(double celsius) {
        vector<double> ans(2);
        ans[0] = celsius + 273.15;
        ans[1] = celsius * 1.80 + 32.00;
        return ans;
        
    }
};

2470. 最小公倍数为 K 的子数组数目

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 nums 的 子数组 中满足 元素最小公倍数为 k 的子数组数目。

子数组 是数组中一个连续非空的元素序列。

数组的最小公倍数 是可被所有数组元素整除的最小正整数。

提示：

• 1 <= nums.length <= 1000
• 1 <= nums[i], k <= 1000

示例

输入：nums = [3,6,2,7,1], k = 6
输出：4
解释：以 6 为最小公倍数的子数组是：

• [3,6,2,7,1]
• [3,6,2,7,1]
• [3,6,2,7,1]
• [3,6,2,7,1]

思路

暴力+gcd。

由于数据范围较小，可以暴力枚举所有的子数组，然后计算子数组的最小公倍数，

// C++
class Solution {
public:
    
    int gcd(int a, int b) {
        return b ? gcd(b, a % b) : a;
    }
    
    int subarrayLCM(vector<int>& nums, int k) {
        int ans = 0, n = nums.size();
        for (int i = 0; i < n; i++) {
            int lcm = nums[i]; // 最小公倍数
            for (int j = i; j < n; j++) {
                lcm = lcm  * nums[j] / gcd(lcm, nums[j]);
                if (lcm == k) ans++;
                else if (lcm > k) break;
            }
        }
        return ans;
    }
};

如果这道题的数据范围较大，则不能用暴力枚举。

可以考虑用双指针，但是从一个区间内去掉一个数，再更新这个区间的最小公倍数，并不是那么好计算，需要用线段树或树状数组进行优化。

一些在区间上的操作是能够合并，也能拆分的。比如一个区间[i, j]的前缀和，从中去掉一个数，或往里添加一个数，都很容易计算出新的前缀和；但是有一些操作是只能合并，无法拆分的，比如一个区间[i, j]的最大值，往里添加一个数，很容易计算出新的最大值，但从中去掉一个数，就无法计算新的最大值了。像这种无法进行拆分的操作，就需要用线段树来进行优化。

2471. 逐层排序二叉树所需的最少操作数目

给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的 层数 是该节点和根节点之间的路径的边数。

提示：

• 树中节点的数目在范围 [1, 10^5] 。
• 1 <= Node.val <= 10^5
• 树中的所有值 互不相同 。

示例

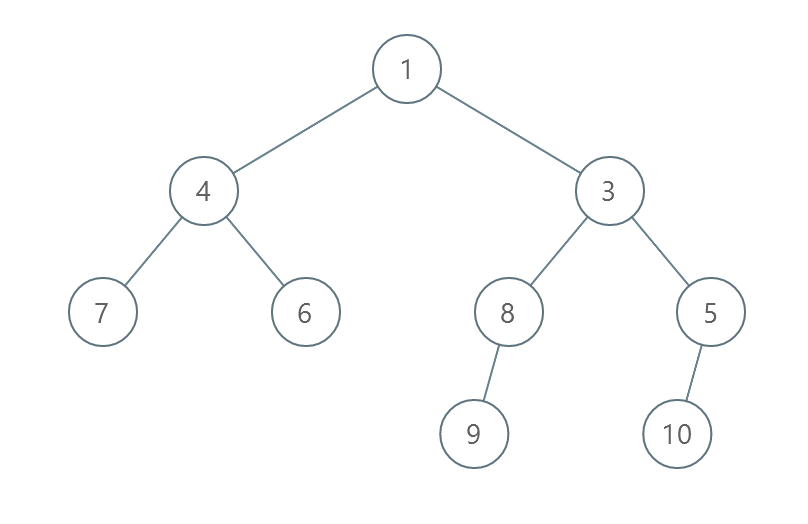
输入：root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出：3
解释：
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作，所以返回 3 。
可以证明 3 是需要的最少操作数目。

思路

层序遍历+选择排序

要将同一层的节点排序，并且要采用交换，且有最小交换次数。我们可以使用选择排序进行模拟，每次将最小的节点交换到最左侧。用一个小根堆来维护未确认位置的点，并用一个指针标记当前需要确认的位置。

// C+++
typedef pair<int, int> PII;
const int N = 1e5 + 10;
class Solution {
public:
    
    int idx_to_val[N];
    
    int val_to_idx[N];
    
    int minimumOperations(TreeNode* root) {
        int ans = 0;
        queue<TreeNode*> q;
        priority_queue<int, vector<int>, greater<int>> heap;
        q.push(root);
        while (q.size()) {
            memset(idx_to_val, -1, sizeof idx_to_val);
            memset(val_to_idx, -1, sizeof val_to_idx);
            int size = q.size();
            for (int i = 0; i < size; i++) {
                auto x = q.front();
                q.pop();
                heap.push(x->val);
                idx_to_val[i] = x->val;
                val_to_idx[x->val] = i;
                if (x->left != nullptr) q.push(x->left);
                if (x->right != nullptr) q.push(x->right);
            }
            // 左侧边界
            int cur = 0;
            while (heap.size()) {
                int x = heap.top();
                heap.pop();
                if (val_to_idx[x] != cur) {
                    int val = x, o_val = idx_to_val[cur];
                    int idx = val_to_idx[x], o_idx = cur;
                    idx_to_val[idx] = o_val;
                    idx_to_val[o_idx] = val;
                    val_to_idx[val] = o_idx;
                    val_to_idx[o_val] = idx;
                    ans++; // 需要交换
                }
                cur++;
            }
        }
        return ans;
    }
};

这道题的另一个经典做法是：置换环。

置换环算法能够求出数组排序需要的最小交换次数。其思想是；对每个元素，将其指向其排序后应该放到的位置，直到首尾相接形成一个环。

具体来说，若一个数，在排序前，其在数组中的位置是a，排序后，其在数组中的位置是b，那么新建一条边，从a指向b，a -> b。那么其实，对于每个位置所代表的点x，其都有一条出边和一条入边。

x的出边指向的点，假设是y，表示：排序前位置x上的数，在排序后其最终的位置是y；

x的入边来自的点，假设是w，表示：排序后最终位置是x的数，其排序前的位置是w。

容易得知，每个位置，该位置原本的数一定会去到一个最终位置（出边），也会有另一个位置的数的最终位置是该位置（入边）。所以，每个位置的出度和入度都不多不少恰好是1。

这样以来，将所有位置表示为点，将位置的关系用边进行连接，那么最终会产生一个或多个首尾相接的环。

当我们交换两个位置的数时，无非有两种情况

• 交换的是同一个环里的两个位置
• 交换的是不同环里的两个位置

我们举一组样例数据：7 1 9 3 2 5 4，

排序前: 7 1 9 3 2 5 4
排序后: 1 2 3 4 5 7 9

按照上述规则，画出的图如下

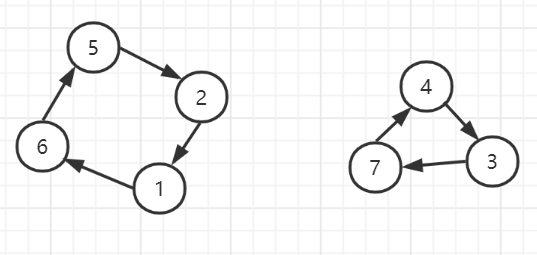
解释如下：

• 排序前位置为1的数是7，排序后最终位置是6，所以1->6
• 排序前位置为2的数是1，排序后最终位置是1，所以2->1
• 排序前位置为3的数是9，排序后最终位置是7，所以3->7
• 排序前位置为4的数是3，排序后最终位置是3，所以4->3
• 排序前位置是5的数是2，排序后最终位置是2，所以5->2
• 排序前位置是6的数是5，排序后最终位置是5，所以6->5
• 排序前位置是7的数是4，排序后最终位置是4，所以7->4

我们尝试交换位置2和位置6（交换同一个环内的2个位置），交换后，更新的图如下

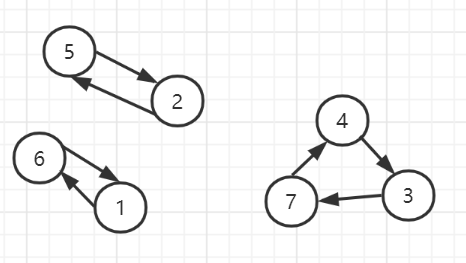
如果我们交换位置3和2（交换不同环中的2给位置），交换后，更新的图如下

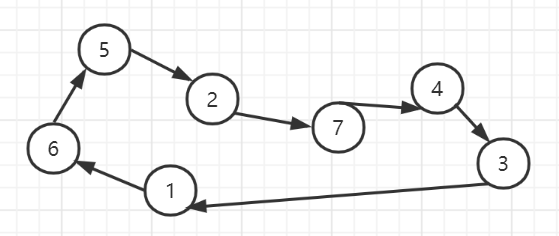
容易得到如下结论：

• 若交换同一个环内的2个位置，会将1个环拆分成2个环
• 若交换不同环内的2个位置，会将2个环合并为1个环

我们最终要得到的状态，是每个位置都是一个自环，即最终要得到n个环。

那么，最少的交换次数，一定是每次交换，都将一个环拆成更小的环，而不是将2个环合并成1个更大的环。

假设一个环内的节点数量为k，则这个环最终将被拆成k个自环，共需要k - 1次拆分，即需要k - 1次交换。

一共有n个环，每个环需要的拆分次数是环中节点的数量减1，则所有环需要的拆分次数就是所有节点的数量减去环的数量。

于是这样就能求出最小的交换次数。

由于这种环图的特殊性，每个环都是首尾相连，所以每个环都是一个连通块。故这道题也可以用并查集来做。我们只要按照上述规则，进行集合的合并，并维护一下连通块的数量，即可求得需要的最小交换次数。

// C++
class Solution {
public:
	// 并查集模板
    int find(int x, vector<int>& p) {
        if (x != p[x]) p[x] = find(p[x], p);
        return p[x];
    }

    int calc(vector<int>& v) {
        int n = v.size();
        // 记录元素和原位置的关系
        unordered_map<int, int> idx;
        // 并查集 parent数组
        vector<int> p(n);
        for (int i = 0; i < n; i++) {
            idx[v[i]] = i;
            p[i] = i;
        }
        sort(v.begin(), v.end());
        // 开始做集合合并
        int cnt = n; // 连通块个数
        for (int i = 0; i < n; i++) {
            int a = i, b = idx[v[i]];
            if (find(a, p) != find(b, p)) {
                p[find(a, p)] = find(b, p);
                cnt--; // 合并后连通块减少一个
            }
        }
        return n - cnt; // 最少交换次数
    }

    int minimumOperations(TreeNode* root) {
        queue<TreeNode*> q;
        q.push(root);
        int ans = 0;
        while (q.size()) {
            int sz = q.size();
            vector<int> v(sz);
            for (int i = 0; i < sz; i++) {
                TreeNode* x = q.front();
                q.pop();
                v[i] = x->val;
                if (x->left != nullptr) q.push(x->left);
                if (x->right != nullptr) q.push(x->right);
            }
            ans += calc(v); // 计算这一层的交换次数
        }
        return ans;
    }
};

2472. 不重叠回文子字符串的最大数目

给你一个字符串 s 和一个 正 整数 k 。

从字符串 s 中选出一组满足下述条件且 不重叠 的子字符串：

• 每个子字符串的长度 至少 为 k 。
• 每个子字符串是一个 回文串 。

返回最优方案中能选择的子字符串的 最大 数目。

子字符串 是字符串中一个连续的字符序列。

提示：

• 1 <= k <= s.length <= 2000
• s 仅由小写英文字母组成

示例

输入：s = "abaccdbbd", k = 3
输出：2
解释：可以选择 s = "abaccdbbd" 中斜体加粗的子字符串。"aba" 和 "dbbd" 都是回文，且长度至少为 k = 3 。
可以证明，无法选出两个以上的有效子字符串。

思路

中心开花+贪心

先求出以每个点为中心的最短回文串，记录其左端点和右端点。然后将这些回文区间按照左端点排个序，随后挨个取出并计数。这是一种贪心的思想，基于的是要想选出的不重叠字符串数量最多，在尽可能要选择长度短的。

// c++
typedef pair<int, int> PII;
class Solution {
public:
    
    bool isPalin(string s, int i, int j) {
        while (i < j) {
            if (s[i] != s[j]) return false;
            i++;
            j--;
        }
        return true;
    }
    
    int maxPalindromes(string s, int k) {
        int n = s.size();
        vector<PII> v; // 存储所有可能的回文
        // 求出以每个点为中心的最短回文
        for (int i = 0; i < n; i++) {
            // 求奇数长度
            int l = i, r = i;
            bool yes = false;
            while (l >= 0 && r < n && s[l] == s[r]) {
                yes = true;
                if (r - l + 1 >= k) break;
                l--;
                r++;
            }
            if (yes && l >= 0 && r < n && s[l] == s[r] && r - l + 1 >= k) v.push_back({l, r}); 
            // 求偶数长度
            l = i;
            r = i + 1;
            yes = false;
            while (l >= 0 && r < n && s[l] == s[r]) {
                yes = true;
                if (r - l + 1 >= k) break;
                l--;
                r++;
            }
            if (yes && l >= 0 && r < n && s[l] == s[r] && r - l + 1 >= k) v.push_back({l, r}); 
        }
        // 将全部的回文排序
        sort(v.begin(), v.end());
        int ans = 0;
        int r = -1; // 维护当前右端点
        for (auto& p : v) {
            if (r == -1) {
                r = p.second;
                ans++;
            } else if (p.first > r) {
                r = p.second;
                ans++;
            }
        }
        return ans;
    }
};

动态规划

也可以直接用动态规划来做，用g[i][j]表示区间[i, j]是否是回文；f[i]表示从[0, i]中能拆出的满足条件的回文串的最大数量。g的状态一共有n^2，计算需要 $O(n^2)$，f的状态也是 n^2，所以总的时间复杂度就是 $O(n^2)$，在这道题的数据范围下大概是 $10^6$，不会超时。

// C++
class Solution {
public:
    int maxPalindromes(string s, int k) {
        int n = s.size();
        // g[i][j] 表示[i, j]是否是回文串, 下标从1开始
        vector<vector<bool>> g(n + 1, vector<bool>(n + 1, false));
        // 状态转移, 区间DP, 需要从小到达枚举区间长度
        for (int len = 1; len <= n; len++) {
            for (int i = 1; i + len - 1 <= n; i++) {
                int j = i + len - 1;
                if (len == 1) g[i][j] = true;
                else if (s[i - 1] == s[j - 1] && (len == 2 || g[i + 1][j - 1])) g[i][j] = true;
            }
        }

        // f[i]表示[1, i]区间选出不重叠的子字符串的最大数量，下标从1开始
        vector<int> f(n + 1, 0);
        for (int i = 1; i <= n; i++) {
            f[i] = f[i - 1]; // 第i个位置不选
            // 第i个位置选上, 则枚举可能的回文串的长度, 回文串长度至少是k
            // 注意这里要枚举到 j = 0
            for (int j = i - k; j >= 0; j--) {
                if (g[j + 1][i]) {
                    f[i] = max(f[i], f[j] + 1);
                }
            }
        }
        return f[n];
    }
};

总结

第三次AK，还是有点小激动的！

T1是模拟；T2是数论；T3是层序遍历+选择排序/置换环；T4是回文串题目，其实是2个问题的组合，1是求回文串，2是求不重叠回文子串的最大数目；可以用中心开花求回文串，并用贪心求答案；也可以用更为朴素的动态规划。