一文带你学习,动态规划算法
- 1.什么是动态规划(DP)
- 2.青蛙跳台阶问题
- 暴力递归解法
- 自顶向下的递归解法
- 自底向上的动态规划解法
- 3.动态规划的解题套路
- 穷举分析
- 确定边界
- 确定最优子结构
- 写出状态转移方程
- 4.经典线性DP:数字三角形
- 5.01背包:摘花生
1.什么是动态规划(DP)
动态规划其实就是,给定一个问题,我们把它拆成一个个子问题,直到子问题可以直接解决。然后呢,把子问题答案保存起来,以减少重复计算。再根据子问题答案反推,得出原问题解的一种方法
一般这些子问题很相似,可以通过函数关系式(DP方程)递推出来。动态规划就致力于解决每个子问题一次,减少重复计算。其核心思想就是:拆分子问题,记住过往,减少重复计算
一个具体的例子:
A : “1+1+1+1+1+1+1+1 =?”
A : “上面等式的值是多少”
B : 计算 “8”
A : 在上面等式的左边写上 “1+” 呢?
A : “此时等式的值为多少”
B : 很快得出答案 “9”
A : “你怎么这么快就知道答案了”
A : “只要在8的基础上加1就行了”
A : “所以你不用重新计算,因为你记住了第一个等式的值为8!动态规划算法也可以说是 ‘记住求过的解来节省时间’”
2.青蛙跳台阶问题
青蛙跳台阶问题

暴力递归解法
要想到第10级台阶,要么是先跳到第9级,然后再跳1级台阶上去;要么是先跳到第8级,然后一次迈2级台阶上去。
同理,要想到第9级台阶,要么是先跳到第8级,然后再跳1级台阶上去;要么是先跳到第7级,然后一次迈2级台阶上去。
要想到第8级台阶,要么是先跳到第7级,然后再跳1级台阶上去;要么是先跳到第6级,然后一次迈2级台阶上去。
假设跳到第n级台阶的跳数我们定义为f(n),很显然就可以得出以下公式:
f(10) = f(9) + f(8)
f (9) = f(8) + f(7)
f (8) = f(7) + f(6)
...
f(3) = f(2) + f(1)
即通用公式为: f(n) = f(n-1) + f(n-2)
那f(2) 或者 f(1) 等于多少呢?显然f(2) = 2,f(1) = 1
于是我们萌生了使用暴力递归解题的方法:
class Solution {
public:
int numWays(int n) {
if(n == 1 || n == 0) {
return 1;
}
if(n == 2) {
return 2;
}
return (numWays(n-1) + numWays(n-2)) % 1000000007;
}
};
一发提交直接TLE:

分析算法的时间复杂度:
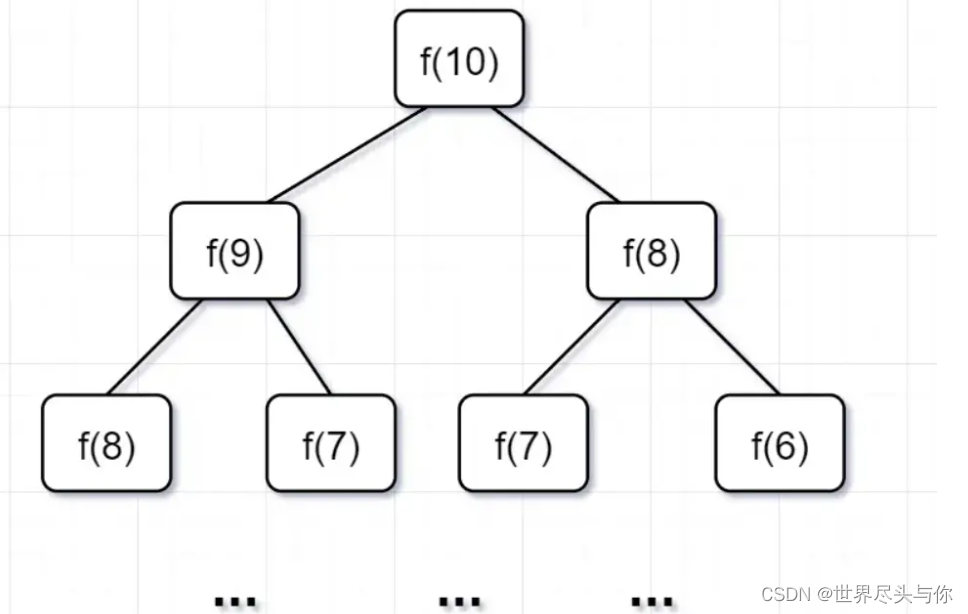
递归时间复杂度 = 解决一个子问题时间(本例为1)*子问题个数
问题个数 = 递归树节点的总数,递归树的总节点 = 2^n-1,所以是复杂度O(2^n)
本题数据范围n的最大值为100,而2的100次方等于1.2676506e+30,惊人的数字!
自顶向下的递归解法
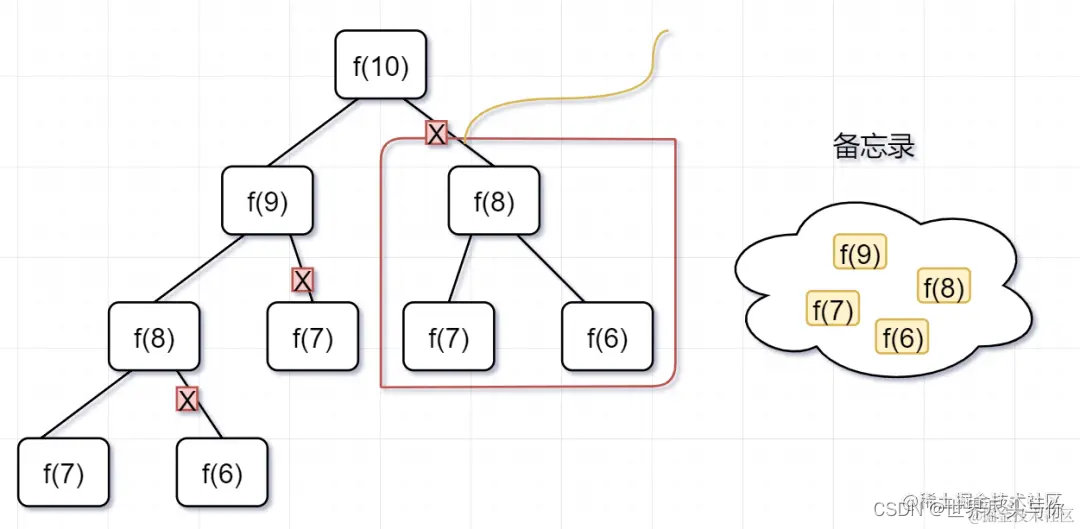
一般使用一个数组或者一个哈希map充当一个备忘录,保存之前求解过的值,避免重复计算
- 第一步,
f(10)= f(9) + f(8),f(9) 和f(8)都需要计算出来,然后再加到备忘录中,如下:
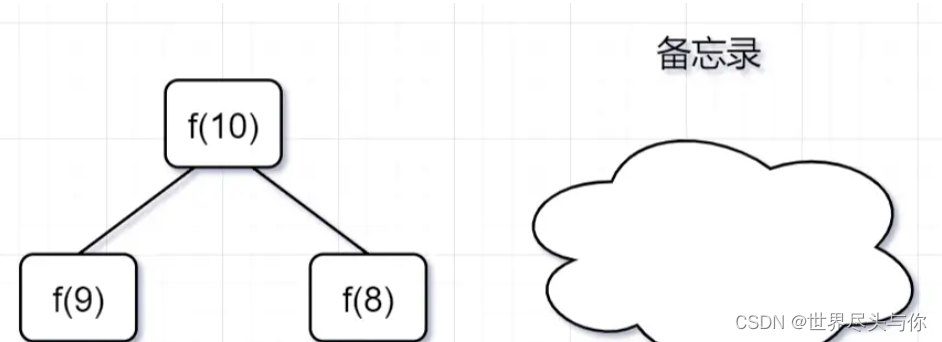
- 第二步,
f(9) = f(8) + f(7),f(8) = f(7) + f(6), 因为 f(8) 已经在备忘录中啦,所以可以省掉,f(7),f(6)都需要计算出来,加到备忘录中
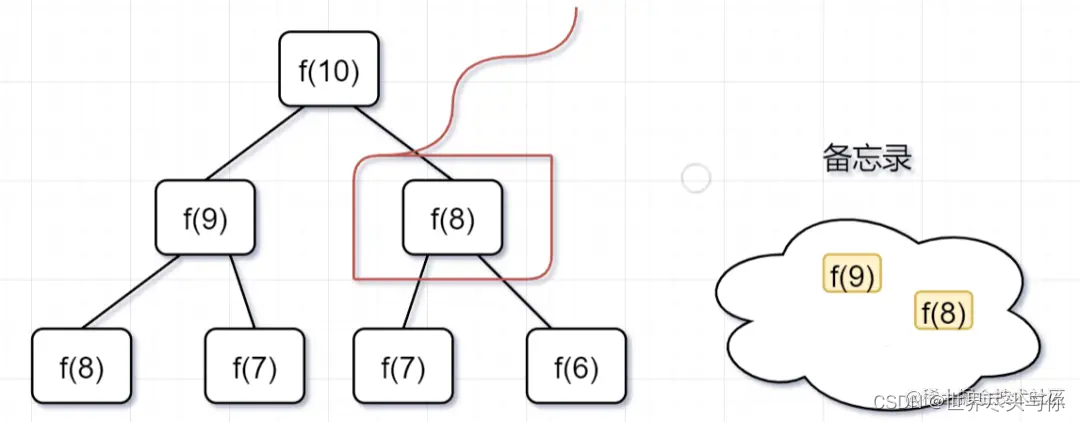
- 第三步,
f(8) = f(7) + f(6),发现f(8),f(7),f(6)全部都在备忘录上了,所以都可以剪掉
实现算法:
class Solution {
public:
int arr[100 + 5]; // 这个数组用作备忘录
int numWays(int n) {
if(n == 1 || n == 0) {
return 1;
}
if(n == 2) {
return 2;
}
if(arr[n] !=0) {
return arr[n];
} else {
arr[n] = (numWays(n - 1) + numWays(n - 2)) % 1000000007;
return arr[n];
}
}
};
自底向上的动态规划解法
动态规划跟带备忘录的递归解法基本思想是一致的,都是减少重复计算,时间复杂度也都是差不多
- 带备忘录的递归,是从f(10)往f(1)方向延伸求解的,所以也称为自顶向下的解法。
- 动态规划从较小问题的解,由交叠性质,逐步决策出较大问题的解,它是从f(1)往f(10)方向,往上推求解,所以称为自底向上的解法。
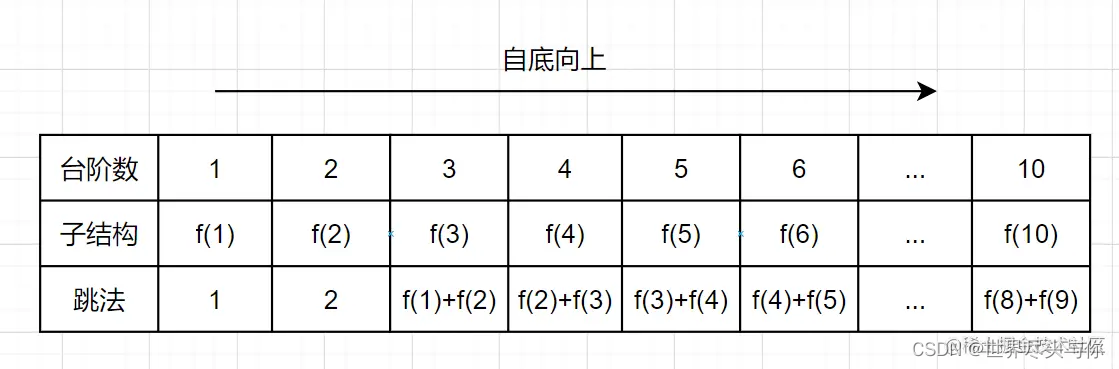
实现算法:
class Solution {
public:
int dp[100 + 5]; // DP数组
int numWays(int n) {
if(n <= 1) {
return 1;
}
dp[0] = 1;
dp[1] = 1;
for(int i = 2 ; i <= n ; i++) {
dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
}
return dp[n];
}
};
算法的世界多么美妙!
3.动态规划的解题套路
如果一个问题,可以把所有可能的答案穷举出来,并且穷举出来后,发现存在重叠子问题,就可以考虑使用动态规划。如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等,都是动态规划的经典应用场景
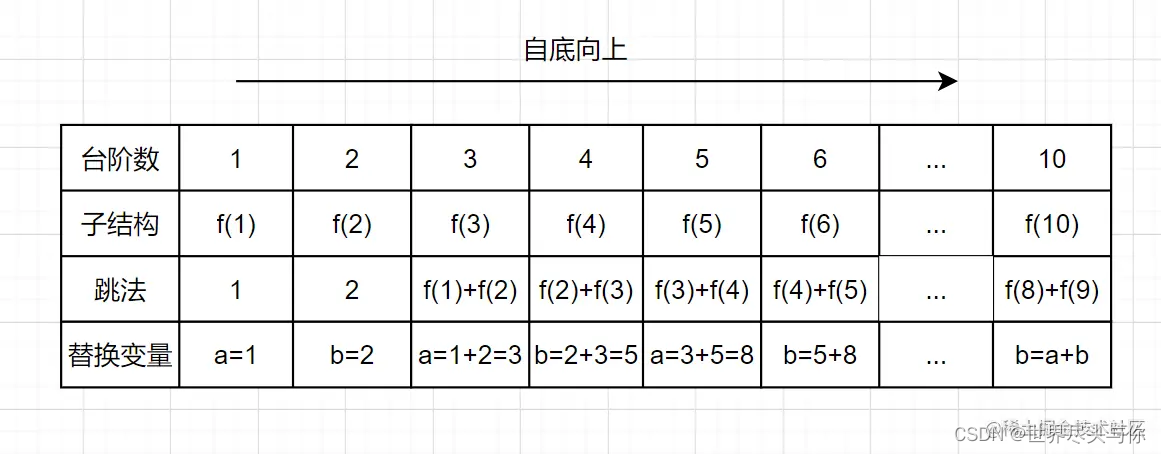
穷举分析
- 当台阶数是1的时候,有一种跳法,
f(1) =1 - 当只有2级台阶时,有两种跳法,第一种是直接跳两级,第二种是先跳一级,然后再跳一级。即
f(2) = 2 - 当台阶是3级时,想跳到第3级台阶,要么是先跳到第2级,然后再跳1级台阶上去,要么是先跳到第 1级,然后一次迈 2 级台阶上去。所以
f(3) = f(2) + f(1) =3 - 当台阶是4级时,想跳到第3级台阶,要么是先跳到第3级,然后再跳1级台阶上去,要么是先跳到第 2级,然后一次迈 2 级台阶上去。所以
f(4) = f(3) + f(2) =5 - …
确定边界
f(1) =1,f(2) = 2就是青蛙跳阶的边界,因为我们可以明确这两个结果的准确值
确定最优子结构
n>=3时,已经呈现出规律 f(n) = f(n-1) + f(n-2) ,因此,f(n-1)和f(n-2) 称为 f(n) 的最优子结构
一道动态规划问题,其实就是一个递推问题。假设当前决策结果是f(n),则最优子结构就是要让 f(n-k) 最优,最优子结构性质就是能让转移到n的状态是最优的,并且与后面的决策没有关系,即让后面的决策安心地使用前面的局部最优解的一种性质
写出状态转移方程

4.经典线性DP:数字三角形
IMUSTACM:数字三角形
本题是一道非常经典且历史悠久的动态规划题,其作为算法题出现,最早可以追溯到 1994 年的 IOI(国际信息学奥林匹克竞赛)的 The Triangle。时光飞逝,经过 20 多年的沉淀,往日的国际竞赛题如今已经变成了动态规划的入门必做题,不断督促着我们学习和巩固算法

在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点,一直走到底层,要求找出一条路径,使路径上的数字的和最大。

穷举分析
要求总路径的最大值,就要求出走到最后一排数字每个数字的最大值,再对最后一排结果取最大值
同时,以2为例,走到它有两种情况,一个是来自左上角f(i-1,j-1)7,一个是来自右上角f(i-1,j)4,事实上,我们只要分析出f(i-1,j-1)和f(i-1,j)那个较大取之即可
同理,对于2左上角的7,走到它有两种情况,一个是来自左上角f(i-1,j-1)8,一个是来自右上角f(i-1,j)1
…
那f(1,1) 等于多少呢?显然f(1,1) =数字三角形的第一个数字
确定边界
f(1,1) =a(1,1)就是数字三角形的边界,因为我们可以明确这两个结果的准确值
确定最优子结构,写出状态转移方程
max(f[i-1][j-1] + a[i][j] , f[i-1][j] + a[i][j])
题解代码:
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int a[N][N],f[N][N];
int main()
{
int n;
scanf("%d",&n);
// 输入数字三角形
for(int i = 1 ;i <= n ; i++)
for(int j = 1 ; j <= i ; j++)
scanf("%d",&a[i][j]);
f[1][1] = a[1][1];
for(int i = 2 ; i <= n ; i++)
for(int j = 1 ; j <= i ; j++)
f[i][j] = max(f[i-1][j-1] + a[i][j] , f[i-1][j] + a[i][j]);
// 求解最后一排数字的最大值得到结果
int res = -0x3f3f3f3f;
for(int i = 1 ; i <= n ; i++)
res = max(res , f[n][i]);
printf("%d",res);
return 0;
}
5.01背包:摘花生
背包问题(Knapsack problem)是一种组合优化的NP完全问题。 问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。 问题的名称来源于如何选择最合适的物品放置于给定背包中。
IMUSTACM:摘花生

题解代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int f[N][N],w[N][N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int t,r,c;
cin >> t;
while(t--)
{
cin >> r >> c;
for(int i = 1 ; i <= r ; i++)
for(int j = 1 ; j <= c ; j++)
cin >> w[i][j];
for(int i = 1 ; i <= r ; i++)
for(int j = 1 ; j <= c ; j++)
f[i][j] = max(f[i-1][j] , f[i][j-1]) + w[i][j];
cout << f[r][c] << endl;
}
return 0;
}
推荐资源:背包九讲