目录
1 相关知识点
2 Matlab完整代码实现
3 结果及可视化

1 相关知识点
这里总结一位博主的目录:梳理如下:
| 粒子群算法(带约束处理)——Python&Matlab实现 |
| 智能优化算法——粒子群算法(Matlab实现) |
| 灰狼算法和粒子群算法比较(附完整Matlab代码)——可应用于电气期刊论文 |
| 粒子群算法求解电力系统环境经济调度+微电网调度(风、光、电动车、柴油机、主网)(Python代码实现) |
| 改进的多目标差分进化算法在电力系统环境经济调度中的应用(Python代码实现)【电气期刊论文复现】 |
| 风电随机性动态经济调度模型(Python&Matlab代码) |
| 多目标灰太狼算法求解环境经济调度问题(IEEE30)(Matlab实现) |
| 多元宇宙算法求解电力系统多目标优化问题(Matlab实现)【电气期刊论文复现】 |
| 求解热电联产经济调度问题的改进遗传与粒子群算法 |
| 改进粒子群算法的配电网故障定位(Python&Matlab代码实现) |
2 Matlab完整代码实现
知识点讲解完毕,下面就是Matlab代码:
clc;
clear;
close all;
%% 经济调度问题
extmodel=CreateModel();
CostFunction=@(x) MyCostExt(x,extmodel); % 成本函数(目标函数)
nVar=extmodel.nPlant; % 发电机台数(决策变量的个数)
VarSize=[1 nVar]; % 决策变量矩阵的大小
VarMin=0; % 变量下限
VarMax=1; % 变量上限
%% 粒子群算法相关参数
MaxIt=100; % 最大迭代次数
nPop=10; % 总群数量
% w=1; % 惯性权重
% wdamp=0.99; % 惯性重量阻尼比
% c1=2; % 个体学习系数
% c2=2; % 种群学习系数
%% 约束系数
phi1=2.05;
phi2=2.05;
phi=phi1+phi2;
chi=2/(phi-2+sqrt(phi^2-4*phi));
w=chi; % 惯性权重
wdamp=1; % 惯性重量阻尼比
c1=chi*phi1; % 个体学习系数
c2=chi*phi2; % 种群学习系数
%% 飞行速度限制
VelMax=0.1*(VarMax-VarMin);
VelMin=-VelMax;
%% 初始化
empty_particle.Position=[];
empty_particle.Cost=[];
empty_particle.Out=[];
empty_particle.Velocity=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
empty_particle.Best.Out=[];
particle=repmat(empty_particle,nPop,1);
BestSol.Cost=inf;
for i=1:nPop
%=====初始化粒子群位置===============
particle(i).Position=unifrnd(VarMin,VarMax,VarSize);
%=====初始化速度======
particle(i).Velocity=zeros(VarSize);
%=====目标函数计算===========
[particle(i).Cost, particle(i).Out]=CostFunction(particle(i).Position);
%====更新粒子个体最优=====
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Out=particle(i).Out;
%====更新粒子群全局最优========
if particle(i).Best.Cost<BestSol.Cost
BestSol=particle(i).Best;
end
end
BestCost=zeros(MaxIt,1);
%% PSO 主循环
for it=1:MaxIt
for i=1:nPop
%============更新速度(跟着公式写就可以啦)===============
particle(i).Velocity = w*particle(i).Velocity ...
+c1*rand(VarSize).*(particle(i).Best.Position-particle(i).Position) ...
+c2*rand(VarSize).*(BestSol.Position-particle(i).Position);
%============适用速度限制============
particle(i).Velocity = max(particle(i).Velocity,VelMin);
particle(i).Velocity = min(particle(i).Velocity,VelMax);
%============更新位置================
particle(i).Position = particle(i).Position + particle(i).Velocity;
IsOutside=(particle(i).Position<VarMin | particle(i).Position>VarMax);
particle(i).Velocity(IsOutside)=-particle(i).Velocity(IsOutside);
%============适用位置限制============
particle(i).Position = max(particle(i).Position,VarMin);
particle(i).Position = min(particle(i).Position,VarMax);
%============计算目标函数===========
[particle(i).Cost, particle(i).Out] = CostFunction(particle(i).Position);
%==========更新个体最优==========
if particle(i).Cost<particle(i).Best.Cost
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Out=particle(i).Out;
%=======更新全局最优============
if particle(i).Best.Cost<BestSol.Cost
BestSol=particle(i).Best;
end
end
end
BestCost(it)=BestSol.Cost;
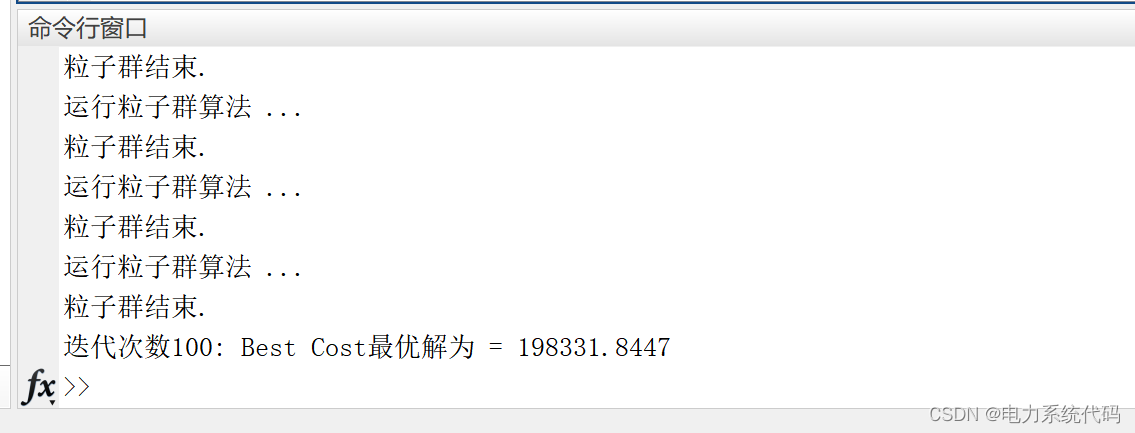
disp(['迭代次数' num2str(it) ': 最优解为 = ' num2str(BestCost(it))]);
w=w*wdamp;
end
%% 结果
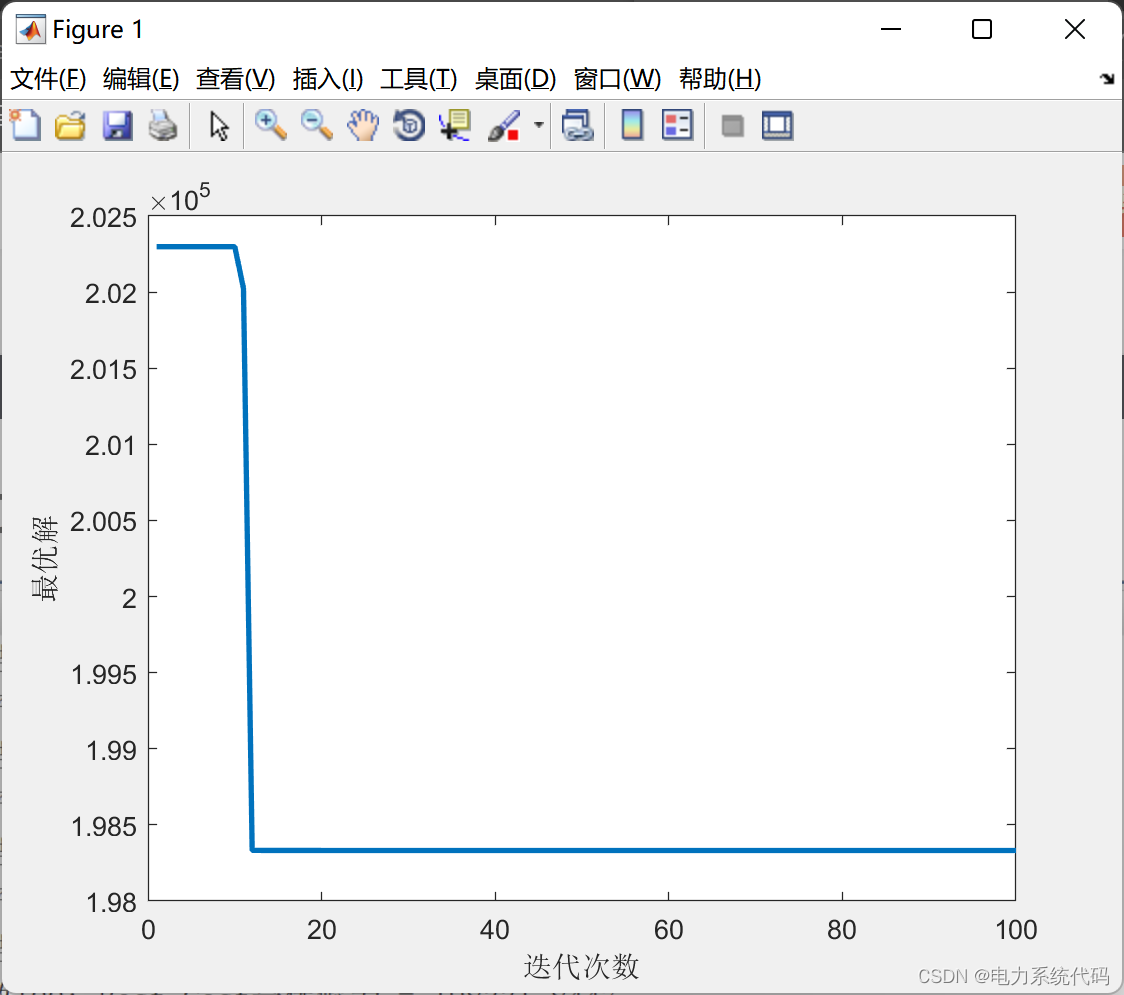
figure;
plot(BestCost,'LineWidth',2);
xlabel('迭代次数');
ylabel('最优解');
function results=RunInternalPSO(intmodel)
disp('运行粒子群算法 ...');
%% 本文参数定义
CostFunction=@(x) MyCost(x,intmodel); % 目标函数
nVar=intmodel.nPlant; %决策变量个数
VarSize=[1 nVar]; % 决策变量矩阵的大小
VarMin=0; %变量下限
VarMax=1; %变量上
%% 粒子群参数
MaxIt=100;
nPop=50;
% w=1;
% wdamp=0.99;
% c1=2;
% c2=2;
%% 约束系数
phi1=2.05;
phi2=2.05;
phi=phi1+phi2;
chi=2/(phi-2+sqrt(phi^2-4*phi));
w=chi;
wdamp=1;
c1=chi*phi1;
c2=chi*phi2;
%% 速度限制
VelMax=0.1*(VarMax-VarMin);
VelMin=-VelMax;
%% 初始化
empty_particle.Position=[];
empty_particle.Cost=[];
empty_particle.Out=[];
empty_particle.Velocity=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
empty_particle.Best.Out=[];
particle=repmat(empty_particle,nPop,1);
BestSol.Cost=inf;
for i=1:nPop
% 初始化位置
particle(i).Position=unifrnd(VarMin,VarMax,VarSize);
% 初始化速度
particle(i).Velocity=zeros(VarSize);
% 目标函数计算
[particle(i).Cost, particle(i).Out]=CostFunction(particle(i).Position);
% 个体最优
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Out=particle(i).Out;
% 全局最优
if particle(i).Best.Cost<BestSol.Cost
BestSol=particle(i).Best;
end
end
BestCost=zeros(MaxIt,1);
%% PSO主循环
for it=1:MaxIt
for i=1:nPop
% 更新速度
particle(i).Velocity = w*particle(i).Velocity ...
+c1*rand(VarSize).*(particle(i).Best.Position-particle(i).Position) ...
+c2*rand(VarSize).*(BestSol.Position-particle(i).Position);
%速度限制
particle(i).Velocity = max(particle(i).Velocity,VelMin);
particle(i).Velocity = min(particle(i).Velocity,VelMax);
% 更新位置
particle(i).Position = particle(i).Position + particle(i).Velocity;
IsOutside=(particle(i).Position<VarMin | particle(i).Position>VarMax);
particle(i).Velocity(IsOutside)=-particle(i).Velocity(IsOutside);
% 位置限制
particle(i).Position = max(particle(i).Position,VarMin);
particle(i).Position = min(particle(i).Position,VarMax);
% 目标函数计算
[particle(i).Cost, particle(i).Out] = CostFunction(particle(i).Position);
%更新个体最优
if particle(i).Cost<particle(i).Best.Cost
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Out=particle(i).Out;
% 更新全局最优
if particle(i).Best.Cost<BestSol.Cost
BestSol=particle(i).Best;
end
end
end
BestCost(it)=BestSol.Cost;
w=w*wdamp;
end
%% 结果
results.BestSol=BestSol;
results.BestCost=BestCost;
disp('粒子群结束.');
endfunction results=RunInternalPSO(intmodel)
disp('运行粒子群算法 ...');
%% 本文参数定义
CostFunction=@(x) MyCost(x,intmodel); % 目标函数
nVar=intmodel.nPlant; %决策变量个数
VarSize=[1 nVar]; % 决策变量矩阵的大小
VarMin=0; %变量下限
VarMax=1; %变量上
%% 粒子群参数
MaxIt=100;
nPop=50;
% w=1;
% wdamp=0.99;
% c1=2;
% c2=2;
%% 约束系数
phi1=2.05;
phi2=2.05;
phi=phi1+phi2;
chi=2/(phi-2+sqrt(phi^2-4*phi));
w=chi;
wdamp=1;
c1=chi*phi1;
c2=chi*phi2;
%% 速度限制
VelMax=0.1*(VarMax-VarMin);
VelMin=-VelMax;
%% 初始化
empty_particle.Position=[];
empty_particle.Cost=[];
empty_particle.Out=[];
empty_particle.Velocity=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
empty_particle.Best.Out=[];
particle=repmat(empty_particle,nPop,1);
BestSol.Cost=inf;
for i=1:nPop
% 初始化位置
particle(i).Position=unifrnd(VarMin,VarMax,VarSize);
% 初始化速度
particle(i).Velocity=zeros(VarSize);
% 目标函数计算
[particle(i).Cost, particle(i).Out]=CostFunction(particle(i).Position);
% 个体最优
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Out=particle(i).Out;
% 全局最优
if particle(i).Best.Cost<BestSol.Cost
BestSol=particle(i).Best;
end
end
BestCost=zeros(MaxIt,1);
%% PSO主循环
for it=1:MaxIt
for i=1:nPop
% 更新速度
particle(i).Velocity = w*particle(i).Velocity ...
+c1*rand(VarSize).*(particle(i).Best.Position-particle(i).Position) ...
+c2*rand(VarSize).*(BestSol.Position-particle(i).Position);
%速度限制
particle(i).Velocity = max(particle(i).Velocity,VelMin);
particle(i).Velocity = min(particle(i).Velocity,VelMax);
% 更新位置
particle(i).Position = particle(i).Position + particle(i).Velocity;
IsOutside=(particle(i).Position<VarMin | particle(i).Position>VarMax);
particle(i).Velocity(IsOutside)=-particle(i).Velocity(IsOutside);
% 位置限制
particle(i).Position = max(particle(i).Position,VarMin);
particle(i).Position = min(particle(i).Position,VarMax);
% 目标函数计算
[particle(i).Cost, particle(i).Out] = CostFunction(particle(i).Position);
%更新个体最优
if particle(i).Cost<particle(i).Best.Cost
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Out=particle(i).Out;
% 更新全局最优
if particle(i).Best.Cost<BestSol.Cost
BestSol=particle(i).Best;
end
end
end
BestCost(it)=BestSol.Cost;
w=w*wdamp;
end
%% 结果
results.BestSol=BestSol;
results.BestCost=BestCost;
disp('粒子群结束.');
end
完整代码:评论区回复关键字
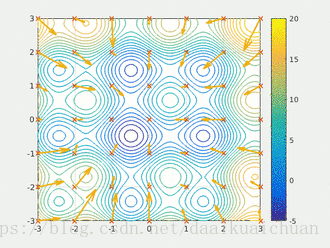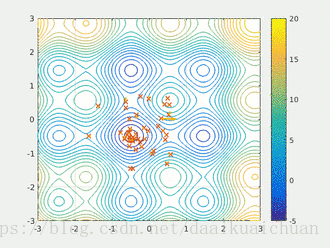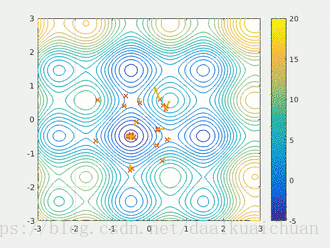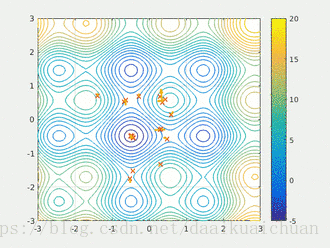
3 结果及可视化