【摘要】容灾设计过程当中需要考虑的故障切换的场景有很多，数据中心内部的高可用切换不在本次讨论范围之内，我们讨论的是容灾恢复过程中的关键跨数据中心级的故障切换场景，从网络层到存储层都会涉及到。（文中涉及相关技术产品参数请以官网最新发布为准）

1. 容灾设计需要进行故障切换的场景

容灾设计过程当中需要考虑的故障切换的场景有很多，数据中心内部的高可用切换不在本次讨论范围之内，我们讨论的是容灾恢复过程中的关键跨数据中心级的故障切换场景，从网络层到存储层都会涉及到，其主要涉及如下几个方面：

① 网络层故障切换（路由、 DNS、交换机、负载均衡 ）。

② 应用服务计算层故障切换（应用 APP ） 。

③ 数据库服务实例层故障切换（数据库 Instance ）。

④ 数据副本层故障切换（数据副本）。

2. 网络层的故障切换策略

2.1 网络流量路径分析

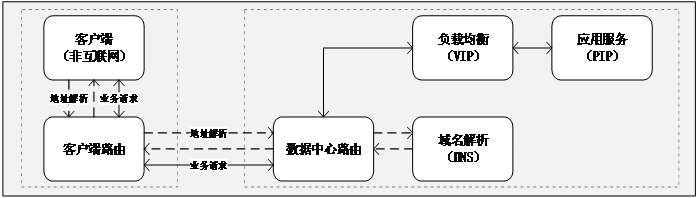
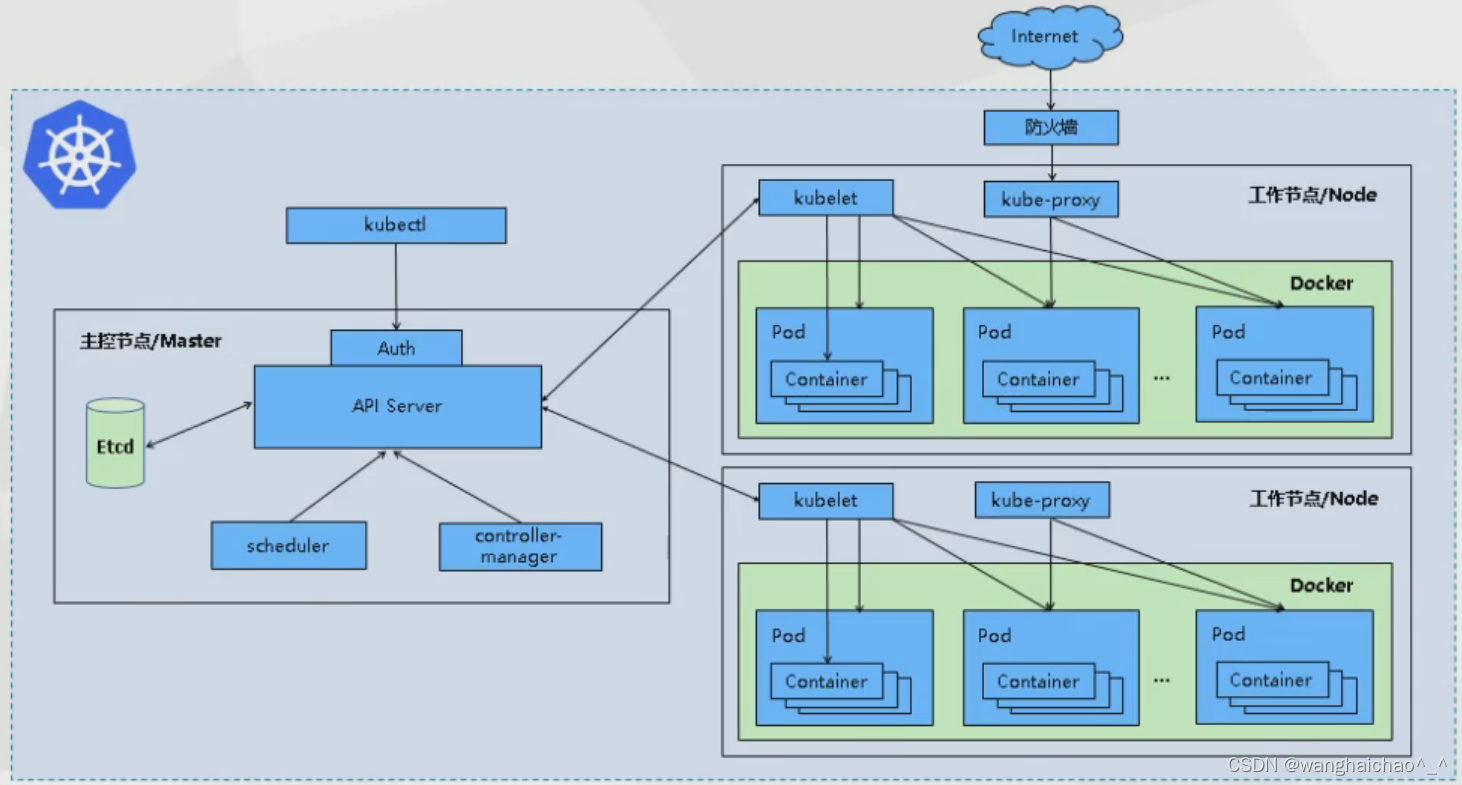
如图所示，来自客户端的流量访问会分为两个过程：

1、客户端需要获取到业务系统的地址信息。通过路由交换机找到域名解析设备得到业务地址信息。

2、客户端利用获取地址和应用服务端口与应用服务建立 Socket连接，然后交互通讯 。

2.2 域名解析层主中心故障场景切换策略