2049. 统计最高分的节点数目-数组树构造+遍历求解最大值数目

给你一棵根节点为 0 的 二叉树 ，它总共有 n 个节点，节点编号为 0 到 n - 1 。同时给你一个下标从 0 开始的整数数组 parents 表示这棵树，其中 parents[i] 是节点 i 的父节点。由于节点 0 是根，所以 parents[0] == -1 。

一个子树的 大小 为这个子树内节点的数目。每个节点都有一个与之关联的 分数 。求出某个节点分数的方法是，将这个节点和与它相连的边全部 删除 ，剩余部分是若干个 非空 子树，这个节点的 分数 为所有这些子树 大小的乘积 。

请你返回有 最高得分 节点的 数目 。

示例 1:

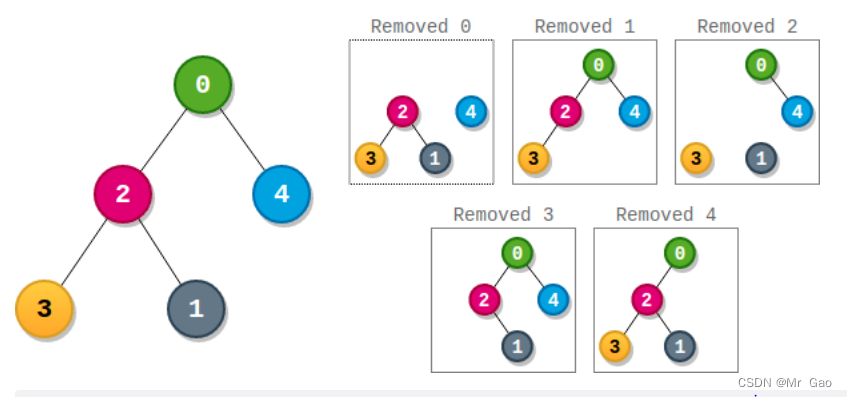
example-1

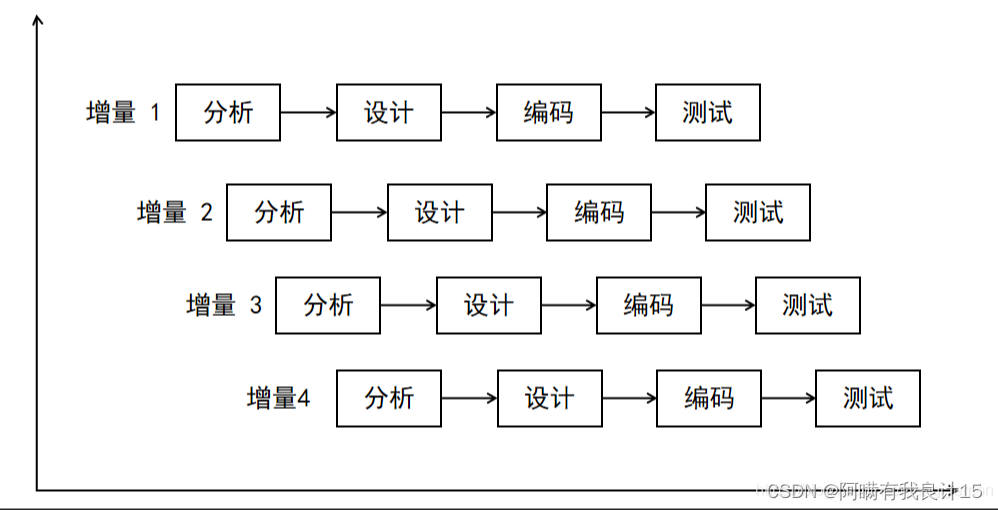
输入：parents = [-1,2,0,2,0]
输出：3
解释：

• 节点 0 的分数为：3 * 1 = 3
• 节点 1 的分数为：4 = 4
• 节点 2 的分数为：1 * 1 * 2 = 2
• 节点 3 的分数为：4 = 4
• 节点 4 的分数为：4 = 4
  最高得分为 4 ，有三个节点得分为 4 （分别是节点 1，3 和 4 ）。

示例 2：

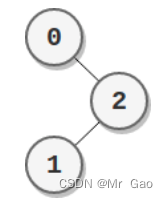
example-2

输入：parents = [-1,2,0]
输出：2
解释：

• 节点 0 的分数为：2 = 2
• 节点 1 的分数为：2 = 2
• 节点 2 的分数为：1 * 1 = 1
  最高分数为 2 ，有两个节点分数为 2 （分别为节点 0 和 1 ）。

对于这一题，博主构造了一个数组树，还是很不错的一个数据结构来处理问题，方便我们的一些工作，感兴趣，可以学习一下，关于这种数组树的构造，时间复杂度O(n) 空间复杂度 O(n),解题代码如下：

int  dfs(int **tree,int now,int * tree_sum){
    if(now!=-1){
        int l=dfs(tree,tree[now][0],tree_sum);
        int r=dfs(tree,tree[now][1],tree_sum);
        tree_sum[now]=1+l+r;

        return l+r+1;


    }
    else{
        return 0;
    }
}
long long max;
int count;
void stasticals_tree(int **tree,int now,int * tree_sum,int pre,int sum){
     if(now!=-1){
          long long pre_sum,left_sum,right_sum;
          if(tree[now][0]!=-1){
               left_sum=tree_sum[tree[now][0]];

          }
          else{
              left_sum=0;

          }
           if(tree[now][1]!=-1){
               right_sum=tree_sum[tree[now][1]];

          }
          else{
              right_sum=0;

          }
          

         if(pre==-1){
                 pre_sum=0;
            }
            else{
                pre_sum=sum-left_sum-right_sum-1;
            

            }
        //  printf("||%d %d %d ",pre_sum,right_sum,left_sum);
     max=fmax(max,fmax(1,pre_sum)*fmax(1,right_sum)*fmax(1,left_sum));
     stasticals_tree(tree,tree[now][0],tree_sum,now,sum);
     stasticals_tree(tree,tree[now][1],tree_sum,now,sum);
   

     }
    
}

void stasticals_treefind(int **tree,int now,int * tree_sum,int pre,int sum){
     if(now!=-1){
          int pre_sum,left_sum,right_sum;
          if(tree[now][0]!=-1){
               left_sum=tree_sum[tree[now][0]];

          }
          else{
              left_sum=0;

          }
           if(tree[now][1]!=-1){
               right_sum=tree_sum[tree[now][1]];

          }
          else{
              right_sum=0;

          }
          

         if(pre==-1){
                 pre_sum=0;
            }
            else{
                pre_sum=sum-left_sum-right_sum-1;
            

            }
      //    printf("||%d %d %d ",pre_sum,right_sum,left_sum);
        if(fmax(1,pre_sum)*fmax(1,right_sum)*fmax(1,left_sum)==max){
            count++;
        }
     stasticals_treefind(tree,tree[now][0],tree_sum,now,sum);
     stasticals_treefind(tree,tree[now][1],tree_sum,now,sum);
   

     }
    
}


int countHighestScoreNodes(int* parents, int parentsSize){
    int **tree=(int **)malloc(sizeof(int *)*parentsSize);
     int *tree_sum=(int *)malloc(sizeof(int )*parentsSize);

  
    for(int i=0;i<parentsSize;i++){
        tree[i]=(int *)malloc(sizeof(int )*2);
        tree[i][0]=-1;
        tree[i][1]=-1;
    }
    for(int i=1;i<parentsSize;i++){
        
        if(tree[parents[i]][0]==-1){
            tree[parents[i]][0]=i;

        }
        else{
            tree[parents[i]][1]=i;
        }
       
    }
    dfs(tree,0,tree_sum);
    //  for(int i=0;i<parentsSize;i++){
    //   //    printf("left rigt %d %d ",tree[i][0],tree[i][1]);
      //    printf("sum %d ",tree_sum[i]);

    //  }
     int sum=tree_sum[0];
      max=0;
      count=0;
     stasticals_tree(tree,0,tree_sum,-1,sum);
     printf("max %d ",max);
     stasticals_treefind(tree,0,tree_sum,-1,sum);


     return count;


}