文章目录
- 1. 树的双亲表示法
- 2. 孩子表示法
- 3. 孩子兄弟表示法(树转化为二叉树)
普通树的存储一半采用三种方式:
- 双亲表示法;
- 孩子表示法;
- 孩子兄弟表示法;
1. 树的双亲表示法
思路和图片来源

采用双亲表示法后的图为:

//顺序存储三叉树的每个节点,数组的值为父节点的下标
//这里练习使用双亲表示法构建层序构建三叉树
#include <vector>
#include <math.h>
#include <assert.h>
template <class T>
struct Elem
{
//每个树节点有两个数据,当前的值个父亲节点的位置
T data;
int parent;
Elem(T data, int parent) : data(data), parent(parent) {}
};
template <class T>
class Tree
{
typedef Elem<T> ElemNode;
public:
Tree(const std::vector<T> &vet)
{
int parent = 0; //第一个父节点
int times = 0; //记录父节点有几个孩子
int level = 0; //记录这是二叉树的第几次
int pos = 0; //记录访问到数组的第几个位置
while (pos < vet.size())
{
if (nodes.empty())
{
//第一个节点
nodes.push_back(ElemNode(vet[pos++], -1));
}
else
{
//计算这层最多可以有几个节点
for (int j = 0; j < pow(3, level - 1); j++)
{
nodes.push_back(ElemNode(vet[pos++], parent));
times++;
if (times == 3)
{
//这里实现的三叉树,所以当这个节点有三个子节点后父亲节点+1
parent++;
times = 0;
}
}
}
level++;
}
}
//获取某个节点的父节点
ElemNode getParent(const T &num)
{
//在数组中查找这个元素
size_t pos = findElem(num);
assert(pos < nodes.size());
return nodes[nodes[pos].parent];
}
std::vector<ElemNode> nodes;
private:
size_t findElem(T num)
{
for (int i = 0; i < nodes.size(); i++)
{
if (nodes[i].data == num)
{
return i;
}
}
return -1;
}
};
#include "Tree.h"
#include <iostream>
using namespace std;
int main(int argc, char const *argv[])
{
Tree<int> tree({1, 2, 3, 4, 5, 6, 7, 8, 9});
cout << tree.getParent(9).data;
return 0;
}

2. 孩子表示法
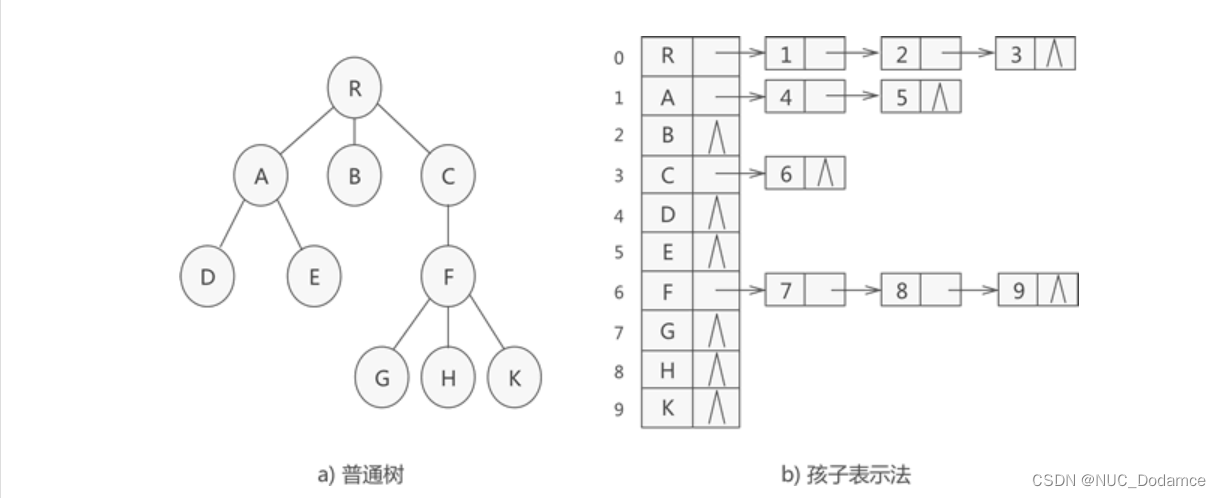
孩子表示法存储普通树采用的是 “顺序表+链表” 的组合结构。
其存储过程是:从树的根节点开始,使用顺序表依次存储树中各个节点。需要注意,与双亲表示法不同的是,孩子表示法会给各个节点配备一个链表,用于存储各节点的孩子节点位于顺序表中的位置。
如果节点没有孩子节点(叶子节点),则该节点的链表为空链表。
/**
孩子表示法存储普通树采用的是 "顺序表+链表" 的组合结构,其存储过程是:从树的根节点开始,使用顺序表依次存储树中各个节点。
需要注意,与双亲表示法不同的是,孩子表示法会给各个节点配备一个链表,用于存储各节点的孩子节点位于顺序表中的位置。
如果节点没有孩子节点(叶子节点),则该节点的链表为空链表。
链表存储的值不是数据本身,而是数据在数组中的位置
*
*/
#include <vector>
#include <iostream>
#include <stdio.h>
#include <assert.h>
struct listNode
{
int pos;
listNode *next = nullptr;
listNode(int _pos) : pos(_pos) {}
};
struct ChildList
{
int data;
listNode *node = nullptr;
ChildList(int _data) : data(_data){};
};
//让用户构建树
class Tree
{
std::vector<ChildList> node;
public:
Tree()
{
std::cout << "输入树的节点个数" << std::endl;
int capacity = 0;
std::cin >> capacity;
int size = 0;
while (size < capacity)
{
std::cout << "输入数组下标" << size << "的值";
int data = 0;
std::cin >> data;
ChildList list(data);
std::cout << "输入这个节点有几个孩子" << std::endl;
int child = 0;
std::cin >> child;
listNode *next = nullptr;
for (int i = 1; i <= child; i++)
{
printf("输入第%d个孩子节点在数组的下标", i);
int pos = 0;
std::cin >> pos;
listNode *node = new listNode(pos);
if (list.node == nullptr)
{
list.node = node;
next = node;
}
else
{
next->next = node;
next = next->next;
}
}
node.push_back(list);
size++;
}
}
//尽可能的表示树结构
void DisPlay()
{
//打印树结构
std::vector<std::vector<int>> msg; //保存树的结构
//读取树每层的结构
std::vector<int> pos(1, 0); //存放下一层节点的位置
std::vector<int> prev;
int max = 0; //记录层最大节点个数
for (int i = 0; i < this->node.size(); i++)
{
std::vector<int> data;
for (int i = 0; i < pos.size(); i++)
{
data.push_back(this->node[pos[i]].data);
}
max = data.size() > max ? data.size() : max;
msg.push_back(data);
//修改存放下一层pos数组
prev = pos;
pos.clear();
for (int i = 0; i < prev.size(); i++)
{
listNode *node = this->node[prev[i]].node;
while (node != nullptr)
{
pos.push_back(node->pos);
node = node->next;
}
}
}
//如果层节点小于max先打印
for (int i = 0; i < msg.size(); i++)
{
int size = msg[i].size();
if (size < max)
{
//打印空格
for (int j = 0; j <= (max - size) / 2; j++)
{
std::cout << " ";
}
}
for (int k = 0; k < size; k++)
{
std::cout << msg[i][k] << " ";
}
std::cout << "\n";
}
}
//查找树节点值data的子节点
void findChild(int data)
{
int pos = findPos(data);
if (pos == -1)
{
printf("树中没有此元素\n");
}
else
{
listNode *list = this->node[pos].node;
printf("%d的子节点值为:\n", data);
while (list != nullptr)
{
std::cout << this->node[list->pos].data << " ";
list = list->next;
}
std::cout << "\n";
}
}
private:
int findPos(int data)
{
for (int i = 0; i < this->node.size(); i++)
{
if (this->node[i].data == data)
{
return i;
}
}
return -1;
}
};
#include "Tree.h"
using namespace std;
int main(int argc, char const *argv[])
{
Tree tree;
tree.DisPlay();
tree.findChild(0);
return 0;
}

3. 孩子兄弟表示法(树转化为二叉树)
所谓孩子兄弟表示法,指的是用将整棵树用二叉链表存储起来.
具体实现方案是:从树的根节点开始,依次存储各个结点的孩子结点和兄弟结点。
在二叉链表中,各个结点包含三部分内容:
- 节点的值;
- 指向孩子结点的指针;
- 指向兄弟结点的指针;
通过孩子兄弟表示法,任意一棵普通树都可以相应转化为一棵二叉树,它们是一一对应的。

/**
所谓孩子兄弟表示法,指的是用将整棵树用二叉链表存储起来.
具体实现方案是:从树的根节点开始,依次存储各个结点的孩子结点和兄弟结点。
在二叉链表中,各个结点包含三部分内容:
1. 节点的值;
2. 指向孩子结点的指针;
3. 指向兄弟结点的指针;
通过孩子兄弟表示法,任意一棵普通树都可以相应转化为一棵二叉树,它们是一一对应的。
*
*/
#include <iostream>
#include <vector>
struct TreeNode
{
char val;
TreeNode *child;
TreeNode *brother;
TreeNode(int _val) : val(_val), child(nullptr), brother(nullptr) {}
};
class Tree
{
public:
TreeNode *root;
Tree()
{
std::vector<TreeNode *> cur_roots; //保存这一层的节点
std::cout << "请输入根节点的值" << std::endl;
char val = 0;
std::cin >> val;
root = new TreeNode(val);
cur_roots.push_back(root);
while (cur_roots.size() != 0)
{
std::vector<TreeNode *> next_roots;
for (int i = 0; i < cur_roots.size(); i++)
{
TreeNode *root = cur_roots[i];
std::cout << "输入" << root->val << "孩子节点个数" << std::endl;
int size = 0;
std::cin >> size;
TreeNode *tail = nullptr;
for (int j = 0; j < size; j++)
{
std::cout << "输入第" << j + 1 << "个孩子节点的值" << std::endl;
char data = 0;
std::cin >> data;
if (j == 0)
{
//第一个节点放到左链表上,代表孩子
root->child = new TreeNode(data);
tail = root->child;
}
else
{
tail->brother = new TreeNode(data);
tail = tail->brother;
}
next_roots.push_back(tail);
}
}
cur_roots = next_roots;
}
}
//最后构造完树后成二叉树,可以直接使用前序遍历
void _PreDisplay(TreeNode *node)
{
if (node == nullptr)
return;
std::cout << node->val << " ";
_PreDisplay(node->child);
_PreDisplay(node->brother);
}
void PreDisplay()
{
_PreDisplay(root);
}
};
#include "Tree.h"
int main(int argc, char const *argv[])
{
Tree tree;
tree.PreDisplay();
return 0;
}