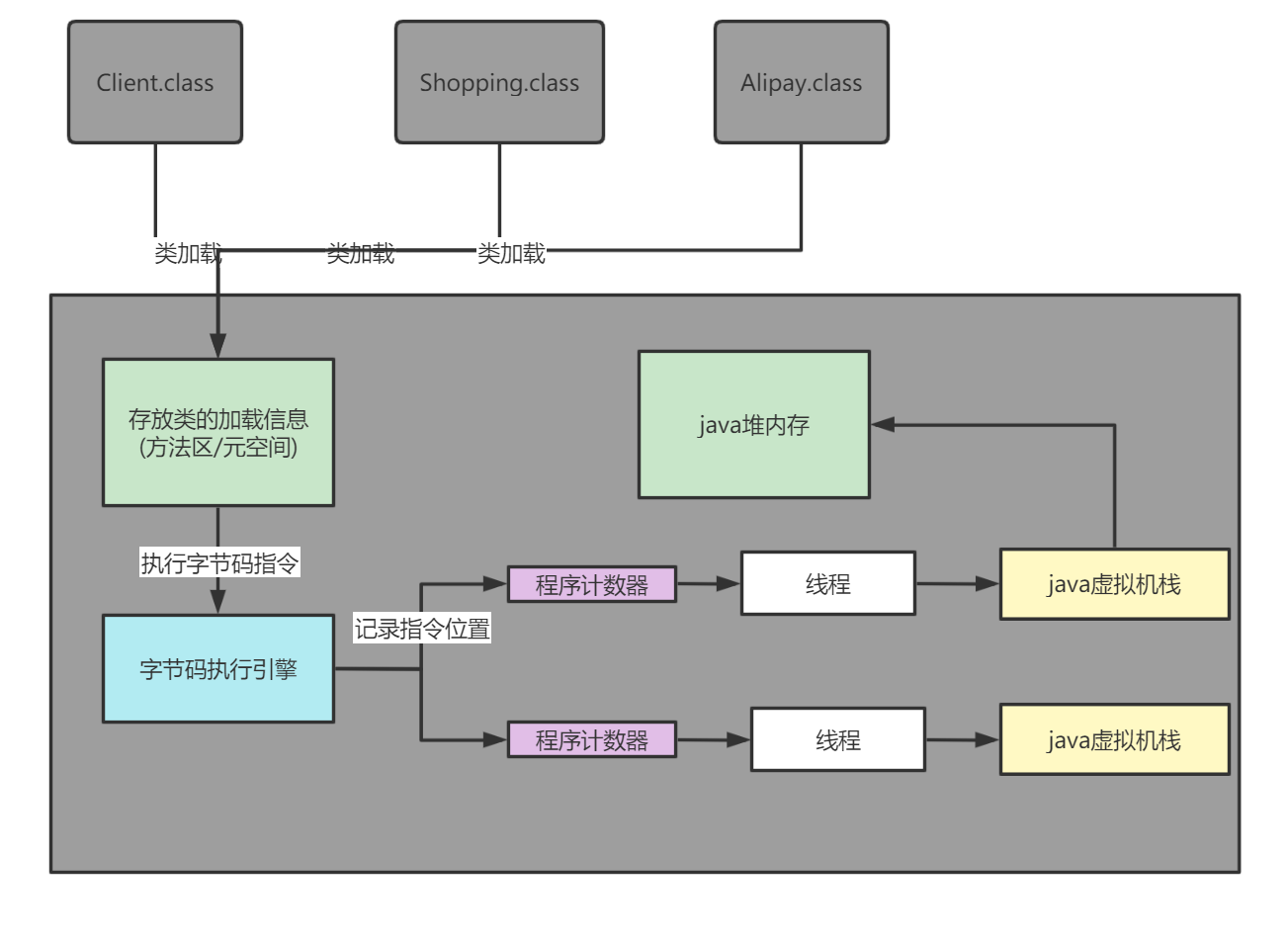
GMC Graph-Based Multi-View Clustering

基于图的多视图聚类

abstract

现有的大多数方法没有充分考虑不同视图的权重，需要额外的聚类步骤来生成最终的聚类。还通常基于所有视图的固定图相似矩阵来优化目标。

本文提出了一种通用的基于图的多视图聚类算法(GMC)来解决上述问题：

• GMC获取所有视图的数据图矩阵，并将其融合生成统一的图矩阵。
• 统一图矩阵反过来又改进了各个视图的数据图矩阵，也直接给出了最终的聚类。

GMC的主要新颖之处在于它的学习方法:

• 它可以帮助各个视图图矩阵的学习和统一图矩阵的学习相互强化。
• 一种新的多视图融合技术可以自动对各个数据图矩阵进行加权，得到统一的图矩阵。
• 对统一矩阵的图拉普拉斯矩阵也施加了不引入调优参数的秩约束，有助于将数据点自然地划分到所需的簇数。
• 提出了一种交替迭代优化算法来优化目标函数。

1.introduction

目前机器学习的主要范式是在单个视图中表示的数据上运行算法。我们称这种范式为单视图学习，因为它不考虑来自其他视图的任何其他相关信息。

我们人类经常从不同的角度看问题。这就是为什么我们可以全面地解决问题。在许多现实生活中的问题中，多视图数据自然而然地出现了。

例如：

例如，同一条新闻可能由不同的新闻机构报道，一幅图像可能由不同类型的特征编码，在网站上分享的一张图片可能有不同的文本描述。所有这些都被称为多视图数据，其中每个单独的视图构成一个学习任务，但每个视图也有其偏见。

多视图数据的自然和频繁的出现孕育了一种新的学习范式，称为多视图学习。多视图聚类对来自多个视图的互补信息进行了探索和利用，从而产生比单视图聚类更准确、更健壮的数据分区。在这些多视图聚类方法中，具有代表性的一类方法是基于图的方法。

图是一种重要的数据结构，用来表示不同类型对象之间的关系。图中的每个节点对应一个对象，每条边代表两个对象之间的关系。一般来说，现实世界中的每个对象都有各种各样的关系图，因为每个对象可以在不同的视图中采样，每个视图的采样数据可以形成一个图。例如，一个作者在不同的书目数据库(如DBLP和IEEE)可能根据他/她的论文有不同的关系图。一个Facebook或Twitter的用户可以根据他/她的个人资料数据库和社交关系组成多个社交网络/图表。

**基于多视图图的聚类方法通常首先在所有视图的输入图中找到一个融合图，然后在这个融合图上使用一个附加的聚类算法，以产生最终的聚类。在这些方法中，每个视图的输入图通常由一个数据相似度矩阵生成，每个矩阵条目表示两个数据点的相似度。**虽然这些方法已经达到了最先进的性能，但它们仍然有一些局限性。

• 有些方法没有考虑不同视图重要性的差异。我们的方法通过自动生成权重来处理差异。
• 许多现有的方法需要额外的聚类步骤来产生融合后的最终聚类。我们的模型在融合中直接产生聚类，不需要额外的聚类步骤。
• 目前大多数方法都是孤立地构建每个视图的图，并在融合过程中保持构建的图固定。我们的方法联合构造各个视图图和融合图。因此，这两个构建过程自然地相互帮助。

在这项工作中，我们同时解决了这些限制，并首次使用联合框架制定了我们的解决方案。

为什么我们需要解决这三个限制?原因如下：

• 首先，样本选择偏差导致观点多样性。
• 第二，额外的聚类步骤带来额外的可能近似正确(PAC)界限。
• 第三，不同的相似度指标对多视图聚类质量有影响。

本文中提出的GMC模型：

GMC不仅可以自动对每个视图进行加权，并在融合后直接生成最终的聚类，而不需要执行任何额外的聚类步骤，而且可以共同构建每个视图的图和融合图，从而相互帮助，相互增强

整体流程图：

具体来说：

1. 首先将每个视图的数据矩阵转换为由相似度图矩阵生成的图矩阵。我们称这个图矩阵为相似诱导图矩阵（SIG）。

2. 然后将提出的融合方法应用于所有视图的SIG矩阵，以便从SIG矩阵学习一个统一的矩阵(即融合图矩阵)U。 U 的学习会自动考虑不同视图 (v) 的不同权重 ($w_v$)。同时，学习到的统一矩阵 U 回去改进每个视图的 SIG 矩阵。还对统一矩阵的拉普拉斯矩阵 $L_U$ 施加秩约束，以约束统一矩阵中的连通分量数等于所需的簇数 c。

因此，我们的模型GMC对各个视图的SIG矩阵进行加权和改进，并同时生成统一的矩阵和最终的聚类

综上所述，本文的贡献：

1. 动机:研究了一种先进的多视图聚类范式，为多视图数据提供了一种新的聚类解决方案。
2. 模型:提出了一种通用的基于图的多视图聚类方法，以解决现有方法的上述局限性。GMC自动对各个视图进行加权，并联合学习各个视图的图和融合图，融合后直接生成最终的聚类。值得注意的是，各个视图图的学习和融合图的学习可以相互帮助。
3. 算法:提出了一种求解GMC问题的交替迭代优化算法，其中每个子问题都有最优解。
4. 结果:实验结果表明，本文提出的GMC方法比现有方法有很大的改进

2.related work

我们的工作还与多视图光谱聚类有关。谱聚类在由数据构成的图上运行，数据点作为节点，它们之间的边作为相似性 。也就是说，谱聚类的输入也是一个相似图。与基于图的聚类的区别在于，谱聚类通常首先找到数据的低维嵌入表示，然后对这个嵌入表示执行 Kmeans 以产生最终的聚类。这样，多视图谱聚类也需要对嵌入表示进行额外的聚类步骤。基于图的聚类在构建的数据图上产生聚类，而不是新的嵌入表示，尽管它们中的大多数仍然需要额外的聚类步骤。我们的方法直接从数据的学习图中获得聚类指标。

多视图聚类总结

3.GRAPH-BASED MULTI-VIEW CLUSTERING

首先对符号做出一些约定：

• 矩阵用黑体大写字母(如X)书写。向量用黑体小写字母(如x)书写。
• 标量使用小写字母
• 对于一个矩阵$X\in R^{d\times n}$，${\mathbf{x}}_{\mathbf{j}}$表示列向量 $x_{ij}$表示第ij个元素
• 对于向量$x\in R^{d\times 1}$,第j个元素记作$x_j$

GMC是包括SIG矩阵构造、多数据图融合和拉普拉斯秩约束的多视图聚类。

3.1 SIG Matrix Construction

对于有m个视图的多视图数据集，让${\mathbf{X}}^1,\dots ,{\mathbf{X}}^{\mathbf{m}}$作为m个视图的数据矩阵。

X v { x 1 v , … , x n v } \mathbf{X^v}\{\mathbf{x_1^v},\dots,\mathbf{x_n^v} \} Xv{x1v​,…,xnv​} 是第v个视图数据

希望构建一个视图的SIG矩阵，使两个数据点之间的距离越小，对应的相似度值就越大，两个数据点之间的距离越大，对应的相似度值就越小(或为零)。为此，我们使用一种稀疏表示方法来构造SIG矩阵。在数学上，我们对这个问题的建模如下:

其中 { S v } \{\mathbf{S^v}\} {Sv} 表示为 { S 1   … , S m } \{\mathbf{S^1}\,\dots,\mathbf{S^m}\} {S1…,Sm}

如果仅有第一项，容易有平凡解，一个为1，其余全是0；如果仅有第二项，则每个元素都是1/n

3.2 Multiple Data Graph Fusion

如第1节所述，我们提出了一个模型，其中每个视图自动加权，SIG矩阵和统一图矩阵联合学习，以相互增强的方式相互帮助。特别,我们通过解决以下优化问题从SIG矩阵 { S 1   … , S m } \{\mathbf{S^1}\,\dots,\mathbf{S^m}\} {S1…,Sm}中计算统一矩阵$\text{U}\in R^{n\times n}$：

$u_i\in R^{n\times 1}$是列向量，$u_{ij}$是${\mathbf{u}}_{\mathbf{i}}$的第j个元素 $w_v$是第v个SIG矩阵${\mathbf{S}}^{\mathbf{v}}$的权值

根据定理1，权值 m = { w 1 , … , w m } \mathbf{m} = \{w_1,\dots,w_m \} m={w1​,…,wm​}是自动确定的。

**定理1。**当权值w固定时，求解问题(4)等价于求解以下问题:

证明：

Eq.(5)的拉格朗日函数如下所示:

$\Lambda$是拉格朗日乘子，第二项是由约束条件导出的形式化术语。

对式(6)对U求导并设导数为零，我们有：

其中：

当wv固定时，Eq.(4)的Lagrange函数的导数等于Eq.(7)，因此Eq.(4)等价于Eq.(5)，权值w也由Eq.(8)确定。

结合问题(3)和问题(4)，通过解决以下问题对S1……Sv和u进行学习:

可以看到，每个SIG矩阵S1……Sm的学习与统一图矩阵U的学习耦合为一个联合问题。这样，两者的学习自然可以互相帮助。

3.3 Multi-View Clustering with Constrained Laplacian Rank

直接在统一图矩阵U上产生聚类结果，无需额外的聚类算法或步骤。到目前为止，通过上文式(9)得到的统一图矩阵U还不能解决这个问题。

现在，我们给出了一个有效而简单的解决方案，通过在统一矩阵U的图拉普拉斯矩阵上施加一个秩约束

$L_U=D_U-(U^T+U)/2$是U的拉普拉斯矩阵

$D_U$是对角矩阵，定义为$D_U={\sum }_j(u_{ij}+u_{ji})/2$

若矩阵U非负：

定理：

拉普拉斯矩阵LU的特征值0的重数c等于矩阵U的图中连通分量的个数。

定理2说如果$rank(L_U)=n-c$，对应的U是将数据点直接划分为c个簇的理想情况。因此，不需要在统一矩阵U上运行额外的聚类算法来生成最终的聚类。根据定理2的启发，我们在问题(4)中添加了一个秩约束，然后我们的多视图聚类模型转化为

上式难以求解，转化为：此处跳步，参考聂飞平自适应聚类

4. OPTIMIZATION ALGORITHMS

约束条件并不顺畅。假设w, S1;……； Sm和F已经得到，我们可以通过增广拉格朗日乘子(ALM)方案计算U。ALM已经在许多矩阵学习问题[56]中显示了它的有效性。类似地，w, S1;……； Sm和F在其他变量固定时更新，这启发我们开发一个交替迭代算法来解决问题(12)。

**固定w,U,F，更新S1,…,Sm,**问题变为：

正如我们所看到的，为每个视图更新Sv是独立的。因此，我们可以逐个更新Sv，表述为：

实际上，我们更倾向于与相邻数据点具有相似之处的数据点。也就是说，我们在sv中学习sv i，有k个非零值，其中k是邻居的数量。具体推导在附录：

固定F,U,S1,…,Sm，更新w:,问题变为：

注意，问题(16)对于不同的i是独立的，因此我们可以对每个i分别求解下面的问题:

记$d_{ij}=||f_i-f_j|{|}_2^2$,问题17变为：

进一步将di表示为第j个元素为dij的向量，ui和si也是如此。定理3揭示了求解问题(18)等价于求解问题(19)

定理3。解决问题(18)相当于解决以下问题:

文章中是反推，根据19反推出17。以下是正推的过程：

固定w,U,S1,…,Sm，更新F:,问题变为：

最优解F由LU的c个特征值对应c个最小特征向量形成。

至此所有的变量已求解完毕！

在实际中，我们初始化SIG矩阵S1;……； Sm首先通过求解问题(3)。注意，为每个视图初始化SIG矩阵是独立的。这里我们以Sv为例