题目描述

有一个物品队列 \frak BB，初始时为空。现在共有三种操作。每个操作会给定三个整数 \mathrm{op},x,yop,x,y，其中 \mathrm{op}op 表示操作种类，x,yx,y 是操作的参数。操作分为如下三种：

• 11：向 \frak BB 尾部添加一个物品，它的体积为 xx，价值为 yy。
• 22：把 \frak BB 尾部最后物品移除。保证此时最少有一个物品。
• 33：有一个体积为 xx 的背包。用 \frak BB 内的物品填充它，每个物品最多用一次，询问最多能获得多大的价值。提示：当 \frak BB 为空时，相当于没有物品可用，答案就是 00。

对于操作 22 和 33，请忽略多余的参数。

本题强制在线。强制在线的方式请见输入格式。

输入格式

• 第一行有两个正整数 n,m_{\max}n,mmax​，表示操作个数以及操作 33 提到的背包的体积的最大值。
• 接下来 nn 行，每行给定三个整数 \mathrm{op},x',y'op,x′,y′。将 x',y'x′,y′ 分别异或上 \mathrm{lastans}lastans 得到该次询问真正的 x,yx,y。其中，\mathrm{lastans}lastans 是上一次操作 33 询问的结果。在第一次操作 33 前，\mathrm{lastans}=0lastans=0。

输出格式

• 输出有若干行，表示每次 33 操作的结果。

输入输出样例

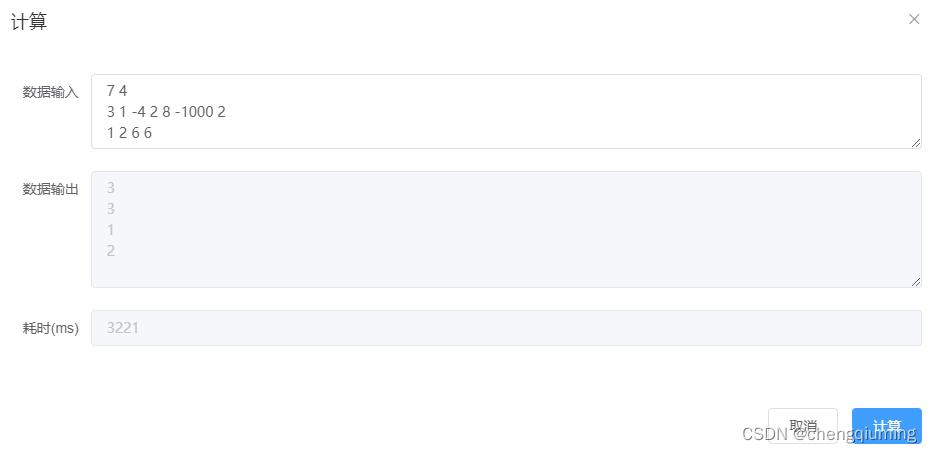
输入 #1复制

10 10
1 3 4
1 5 5
3 4 1
3 12 5
1 14 3
3 1 8
2 11 11
3 2 11
2 8 8
3 12 8

输出 #1复制

4
9
10
9
4

说明/提示

样例解释

解码后的输入数据为：

10 10
1 3 4
1 5 5
3 4 1
3 8 1
1 7 10
3 8 1
2 1 1
3 8 1
2 1 1
3 5 1

对于十次操作，物品序列的情况如下；

• 加入体积为 33，价值为 44 的物品。物品序列为 \{(3,4)\}{(3,4)}。
• 加入体积为 55，价值为 55 的物品。物品序列为 \{(3,4),(5,5)\}{(3,4),(5,5)}。
• 查询体积为 44 的背包能装下的物品价值最大值。此时只能装第一个物品，于是答案为 44。
• 查询体积为 88 的背包能装下的物品价值最大值。此时可把两个物品都装下，答案为 99。
• 加入体积为 77，价值为 1010 的物品。物品序列为 \{(3,4),(5,5),(7,10)\}{(3,4),(5,5),(7,10)}。
• 查询体积为 88 的背包能装下的物品价值最大值。此时直接装第三个物品获得的价值大于装下另外两个，于是答案为 1010。
• 删除最后一个物品。此时物品序列为 \{(3,4),(5,5)\}{(3,4),(5,5)}。
• 查询体积为 88 的背包能装下的物品价值最大值。此时可把两个物品都装下，答案为 99。
• 删除最后一个物品。此时物品序列为 \{(3,4)\}{(3,4)}。
• 查询体积为 55 的背包能装下的物品价值最大值。此时只有一个物品可装，答案为 44。

数据范围及约定

对于全部数据，1\le n\le 3\times 10^41≤n≤3×104，1\le m_{\max}\le 2\times 10^41≤mmax​≤2×104，1\le x, y\le 2\times 10^41≤x,y≤2×104。

首先来个内存不通过的代码：使用暴力dfs

import java.util.*;

import java.util.Scanner;

public class Main {
	
	public static Integer n;
	public static Integer max;
	public static Integer x[];
	public static Integer y[];
	public static Integer op[];
	public static Integer zt[];
	public static Integer num = 0;
	public static Integer lastans = 0;
	public static List<Integer> listx = new ArrayList<>();
	public static List<Integer> listy = new ArrayList<>();
	
	public static void main(String[] args) {
		
		Scanner sca = new Scanner(System.in);
		n = sca.nextInt();
		max = sca.nextInt();
		x = new Integer[n];
		y = new Integer[n];
		op = new Integer[n];
		zt = new Integer[n];
		for(int i = 0;i<n;i++) {
			op[i] = sca.nextInt();
			x[i] = sca.nextInt();
			y[i] = sca.nextInt();
			zt[i] = 0;
		}
		
//		解码数据
		
		for(int i = 0;i<n;i++) {
			x[i] = x[i]^lastans;
			y[i] = y[i]^lastans;
//			System.out.println(x[i]+" "+y[i]+"");
			if(op[i]==1) {
				listx.add(x[i]);
				listy.add(y[i]);
			}else if (op[i]==2) {
				if(listx.size()>1) {
					listx.remove(listx.size()-1);
					listy.remove(listy.size()-1);
				}
			}else if (op[i]==3) {
//				搜寻最大的价值
				dfs(x[i],0);
				System.out.println(num);
				lastans = num;
				num = 0;
//				System.out.println(maxs);
			}
			
//			System.out.println(x[i]+","+y[i]+" :"+listx+" "+listy);
		}
		
	}
//	剩余当前背包mx 4 当前背包内价值my 第几个物品的索引index 
	public static int dfs(Integer mx,Integer my) {
		if(listx.size()==0) {
			return 0;
		}
		for(int i = 0;i<listx.size();i++) {
			if(zt[i]==0) {//如果这个没在包内
//				System.out.println("zt.get(i)："+zt[i]);
				if(mx>=listx.get(i)) {//这个包是否能装下该物品
					mx = mx-listx.get(i);//剩余容量
					my = my+listy.get(i);//当前价值
					if(my>num) {//存储最大的有效价值
						num = my;
					}
					zt[i]=1;
//					进行下一个搜索
					dfs(mx, my);
					mx = mx+listx.get(i);//剩余容量
					my = my-listy.get(i);//当前价值
					zt[i]=0;
				}else {
					zt[i] = 1;
//					进行下一个搜索
					dfs(mx, my);
					zt[i] = 0;
				}
			}
		}
		return 0;
	}

}

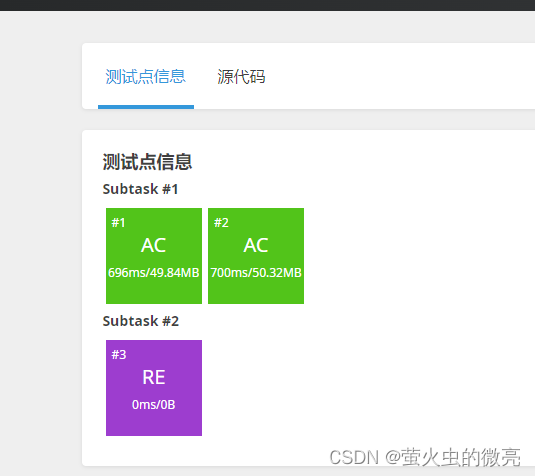
对代码进行优化 ,不会了...

 

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

import java.util.*;

public class Main {
	
	public static List<Integer> listx = new ArrayList<>(),listy = new ArrayList<>();//存放大小 价值
	
	public static int dp[][],dp1[],dp2[],m;
	
	public static void main(String[] args)  throws IOException {
		BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
		int lastans = 0;
	    String s = reader.readLine();
	    int n = Integer.parseInt(s.split(" ")[0]);//一共几行
	    int max = Integer.parseInt(s.split(" ")[1]);//背包体积最大值
	    int ma = 0;
	    dp1 = new int[max+1];
	    dp2 = new int[max+1];
	    for(int i=0;i<n;i++) {
	    	String s1 = reader.readLine();
			int op = Integer.parseInt(s1.split(" ")[0]);//编号类型
			int x = Integer.parseInt(s1.split(" ")[1]);//空间
			int y = Integer.parseInt(s1.split(" ")[2]);//价值
			x = x^lastans;
			y = y^lastans;
			
			if(op==3) {
				lastans = dp1[x];
				System.out.println(dp1[x]);
			}else if(op==1){
				for(int j = max;j>=x;j--) {
					dp1[j] = Math.max(dp1[j], dp1[j-x]+y);
				}
			}else if(op==2){
				for(int j = max;j>=x;j--) {
					dp1[j] = Math.min(dp1[j], dp1[j-x]-y);
				}
			}


			
	    }
	}
	
	
}