1. 树是什么?
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合
注意:根结点没有前驱结点;每棵子树的跟结点有且只有一个前驱结点,可能有0个或者多个后继结点;树是递归定义的;树形结构中,子树之间不能有交集
2. 树的相关概念
结点的度:结点的子树的个数
叶子结点或终端结点:度为0的结点
非终端结点或分支结点:度不为0的点
双亲结点或父结点:若一个节点含有子节点,则这个节点称为其子节点的父节点
孩子结点或子结点:父结点的后继结点
兄弟结点:具有相同父结点的结点
树的度:所有结点中的最大度
结点的层次:从根开始,根为第一层,根的子结点为第二层…
树的高度或深度:树中结点的最大层次
堂兄弟结点:双亲在同一层的结点
结点的祖先:从根到该结点所经分支上的所有结点
子孙:以某节点为根的子树中任一节点
森林:由m(m>0)棵互不相交的树的集合称为森林
3. 树的结构
typedef int TreeDataType;
struct TreeNode
{
TreeDataType data;
struct TreeNode* child;
struct TreeNode* brother;
}
//左孩子右兄弟表示法
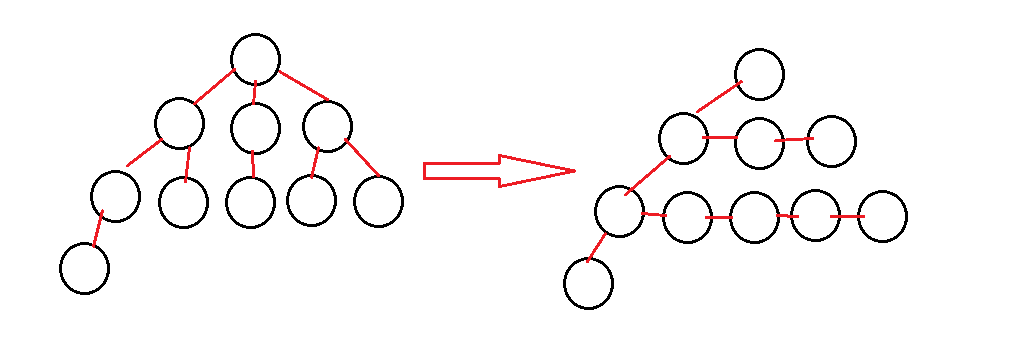
了解:树的应用:Linux树状目录结构
4. 二叉树是什么?
二叉树不存在度大于2的结点 ,二叉树的子树有左右之分,次序不能颠倒
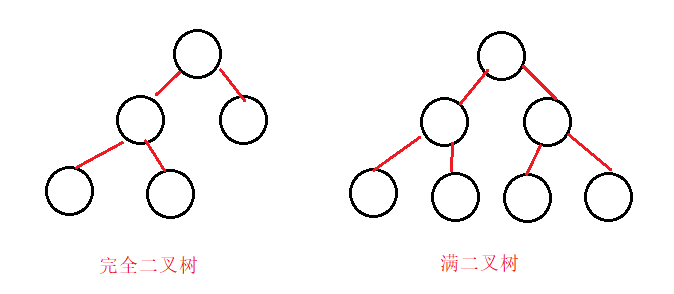
满二叉树:分支结点的度都为2
完全二叉树:前N-1层是满二叉树,最后一层可以不满,但是必须从左到右是连续的
5. 二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 ==2(i-1)===个结点
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 2h-1
- 对任何一棵二叉树, 如果度为0其叶结点个数为N0 , 度为2的分支结点个数为N2 ,则有N0=N2 +1
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log2(n+1)
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
6. 堆是什么?
把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,小堆就是逐层递增,大堆就是递减
7. 堆的性质
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一课完全二叉树
8. 堆的结构
typedef int HeapDataType;
typedef struct heap
{
HeapDataType* a; //数组
int size;
int capacity; //容量
}heap;
9. 堆的初始化
//传指针对结构体内容进行修改
void HeapInit(heap* pheap)
{
assert(pheap);
pheap->a = NULL;
pheap->size = 0;
pheap->capacity = 0;
}
10. 堆的销毁
void HeapDestroy(heap* pheap)
{
assert(pheap);
free(pheap->a);
pheap->a = NULL;
pheap->size = pheap->capacity = 0;
}
11. 向堆中插入数据
//交换数据
void SwapData(HeapDataType* a, HeapDataType* b)
{
HeapDataType tmp = *a;
*a = *b;
*b = tmp;
}
//向上调整
void AdjustUp(HeapDataType* a, int child)
{
int parent = (child - 1) / 2;
//父节点和child结点进行比较判断是否交换
while (child > 0)
{
if (a[child] > a[parent])
{
SwapData(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//尾插建大堆
void HeapPush(heap* pheap, HeapDataType x)
{
assert(pheap);
//扩容问题
if (pheap->size == pheap->capacity)
{
int newCapacity = pheap->capacity == 0 ? 4 : (pheap->capacity) * 2;
HeapDataType* tmp = (HeapDataType*)realloc(pheap->a, sizeof(HeapDataType) * newCapacity);
if (tmp == NULL)
{
perror("HeapPush: malloc is failed!\n");
exit(-1);
}
pheap->a = tmp;
pheap->capacity = newCapacity;
}
pheap->a[(pheap->size)++] = x;
//向上调整
AdjustUp(pheap->a, pheap->size - 1);
}
思路:
尾插一个数据,然后和父结点位置上的数据进行比较,子结点位置数据大于父结点位置数据就交换,当到根结点位置就停止(也就是下标为0的位置就是根节点)
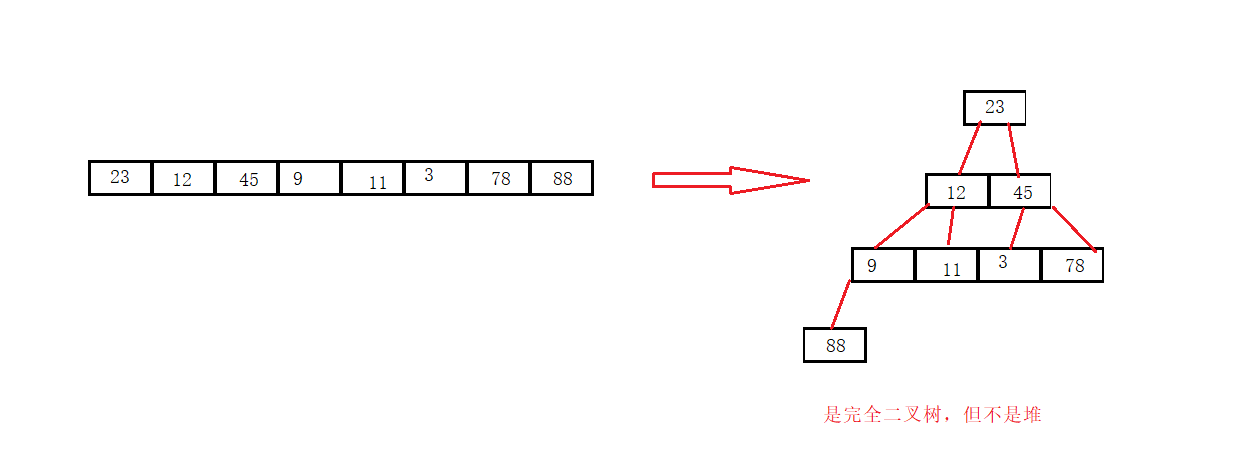
任何数组都可以组成完全二叉树,但不一定是堆。怎么理解?
12. 删除堆顶数据
//交换数据
void SwapData(HeapDataType* a, HeapDataType* b)
{
HeapDataType tmp = *a;
*a = *b;
*b = tmp;
}
//向下调整
//假设方法
void AdjustDown(HeapDataType* a, int size, int parent)
{
//假设默认左孩子大
int lchild = parent * 2 + 1;
while (lchild < size )
{
//确认指向大的孩子
if (lchild + 1 < size && a[lchild + 1] > a[lchild])
{
++lchild;
}
//大堆
//lchild + 1 < size 表示最后的父节点和左孩子对比
if (a[parent] < a[lchild])
{
SwapData(&a[parent], &a[lchild]);
parent = lchild;
lchild = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapPop(heap* pheap)
{
assert(pheap);
assert(pheap->size > 0);
//堆顶数据和堆尾数据交换并删除堆尾(此时堆尾数据也就是堆顶数据)
SwapData(&pheap->a[0], &pheap->a[pheap->size - 1]);
pheap->size--;
//向下调整
AdjustDown(pheap->a, pheap->size, 0);
}
思路:
先交换首尾数据,大堆就是最大数据放在尾部,小堆就是最小的数据放在尾部;然后对前size-1个元素再次从最后的结点的父结点进行大堆调整
13. 获取堆顶数据
HeapDataType HeapTop(heap* pheap)
{
assert(pheap);
//堆中必须有元素
assert(pheap->size > 0);
return pheap->a[0];
}
14. 数据总个数
int HeapSize(heap* pheap)
{
assert(pheap);
return pheap->size;
}
15. 判断堆是否为空
bool HeapEmpty(heap* pheap)
{
assert(pheap);
return pheap->size == 0;
}
16. 不用初始化可以用创建
//a是数组,需要传进数组
void HeapCreate(Heap* heap, HPDataType* a, int size)
{
assert(heap);
heap->a = (HPDataType*)malloc(sizeof(HPDataType) * size);
if (heap->a == NULL)
{
perror("HeapCreate:realloc is failed!\n");
exit(-1);
}
heap->capacity = heap->size = n;
//把数组a的数据拷贝放进heap->a中,这样堆结构体中才有有效值
memcpy(heap->a, a, sizeof(HPDataType) * size);
//向下调整
//(size-1-1)/2为最后一个元素的父结点(从最后的元素向前依次开始向下调整)
for (int i = (size - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(heap->a, size, i);
}
}