一问题描述

黑盒子代表一个原始数据库，存储一个整数数组和一个特殊的 i 变量。最初的时刻，黑盒子是空的，i=0，黑盒子处理一系列命令（事务）。有两种类型的事务。

① ADD(x)，将元素 x 放入黑盒子中。

② GET，将 i 增加1，并给出包含在黑盒子中的所有整数中第 i 小的值。第 i 小的值是黑盒子中按非降序排序后第 i个位置的数字。

示例如下：

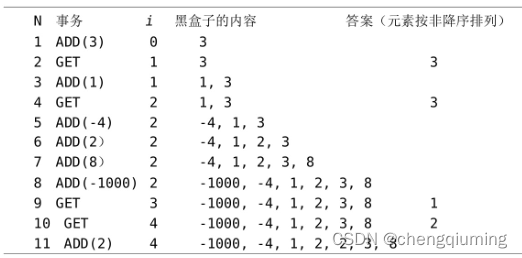
写一个有效的算法来处理给定的事务序列。ADD 和 GET事务的最大数量均为 30000，用两个整数数组来描述事务的顺序：

① A(1), A(2),…,A(M )，包含黑盒子中的一系列元素，A 值是绝对值不超过 2 000 000 000 的整数，M≤30000，对上面的示例，序列A=(3, 1,-4, 2,8,-1000, 2)；

② u(1), u(2), …,u (N)，表示在第 1 个、第 2 个，以此类推，直到第 N 个 GET事务时包含在黑盒子中的元素个数。对上面的示例，u=(1, 2, 6, 6）。假设自然数序列 u(1), u(2), …, u(N ) 按非降序排序，则对 u 序列的第 p 个元素执行 GET 事务，实际上是找 A(1), A(2), …, A(u(p)) 序列中第 p 小的数。

二输入和输出

1 输入

输入包含（按给定顺序）M , N , A(1), A(2), …, A(M), u (1), u (2), …, u (N )。

2 输出

按照给定的事务顺序输出答案序列，每行一个数字。

三输入和输出样例

1 输入样例

7 4

3 1 -4 2 8 -1000 2

1 2 6 6

2 输出样例

3

3

1

2

四分析和设计

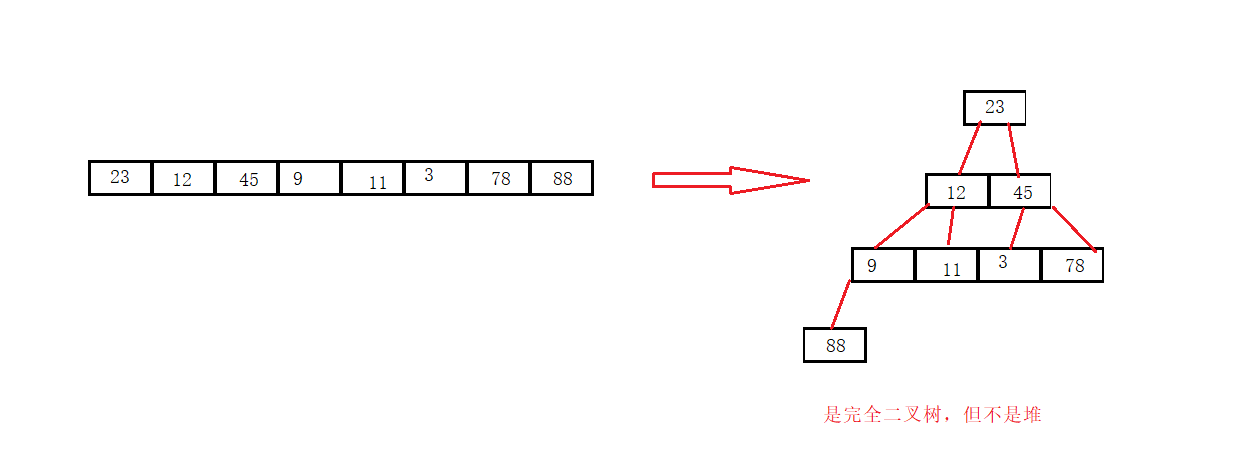
可以创建平衡二叉树，查找第 k 小，采用 Treap 解决。

本问题要控制黑盒子中的元素数量，然后查询第 k 小。u =(1, 2, 6, 6），在黑盒子中有 1 个数时查询第 1 小；在黑盒子中有 2 个数时查询第 2小；在黑盒子中有 6 个数时查询第 3 小；在黑盒子中有 6 个数时查询第 4 小。

五代码

package com.platform.modules.alg.alglib.poj1442;

import java.util.Random;

public class Poj1442A {
    public String output = "";

    private int maxn = 30010;
    int num[] = new int[maxn];
    int num1[] = new int[maxn];
    int n, cnt, root; //结点数，结点存储下标累计，树根
    private node tr[] = new node[maxn];

    public Poj1442A() {
        for (int i = 0; i < tr.length; i++) {
            tr[i] = new node();
        }
    }

    public String cal(String input) {
        int n, a, b, m;
        String[] line = input.split("\n");
        String[] nums = line[0].split(" ");
        n = Integer.parseInt(nums[0]);
        m = Integer.parseInt(nums[1]);

        String[] elements = line[1].split(" ");
        String[] element1s = line[2].split(" ");

        root = 0;
        for (int i = 1; i <= n; i++) {
            num[i] = Integer.parseInt(elements[i - 1]);
        }

        for (int i = 1; i <= m; i++) {
            num1[i] = Integer.parseInt(element1s[i - 1]);
        }

        int t = 1, k = 1;
        while (t <= m) {
            while (k <= num1[t]) {
                root = Insert(root, this.num[k]);
                k++;
            }
            int ans = Findkth(root, t++);
            output += ans + "\n";
        }
        return output;
    }

    // 生成新结点
    int New(int val) {
        tr[++cnt].val = val;
        tr[cnt].pri = Math.abs(new Random().nextInt()) % 100;
        tr[cnt].num = tr[cnt].size = 1;
        tr[cnt].rc = tr[cnt].lc = 0;
        return cnt;
    }

    // 更新子树大小
    void Update(int p) {
        tr[p].size = tr[tr[p].lc].size + tr[tr[p].rc].size + tr[p].num;
    }

    // 右旋
    int zig(int p) {
        int q = tr[p].lc;
        tr[p].lc = tr[q].rc;
        tr[q].rc = p;
        tr[q].size = tr[p].size;
        Update(p);
        // 现在 q 为根
        p = q;
        return p;
    }

    // 左旋
    int zag(int p) {
        int q = tr[p].rc;
        tr[p].rc = tr[q].lc;
        tr[q].lc = p;
        tr[q].size = tr[p].size;
        Update(p);
        // 现在 q 为根
        p = q;
        return p;
    }

    // 在 p 的子树插入值 val
    int Insert(int p, int val) {
        if (p == 0) {
            p = New(val);
            return p;
        }
        tr[p].size++;
        if (val == tr[p].val) {
            tr[p].num++;
            return p;
        }
        if (val < tr[p].val) {
            tr[p].lc = Insert(tr[p].lc, val);
            if (tr[p].pri < tr[tr[p].lc].pri)
                p = zig(p);
        } else {
            tr[p].rc = Insert(tr[p].rc, val);
            if (tr[p].pri < tr[tr[p].rc].pri)
                p = zag(p);
        }
        return p;
    }

    // 求第 k 小的数
    int Findkth(int p, int k) {
        if (p == 0) return 0;
        int t = tr[tr[p].lc].size;
        if (k < t + 1) return Findkth(tr[p].lc, k);
        else if (k > t + tr[p].num) return Findkth(tr[p].rc, k - (t + tr[p].num));
        else return tr[p].val;
    }
}

class node {
    int lc, rc; // 左右孩子
    int val, pri; // 值，优先级
    int num, size; // 重复个数，根的子树的大小
}