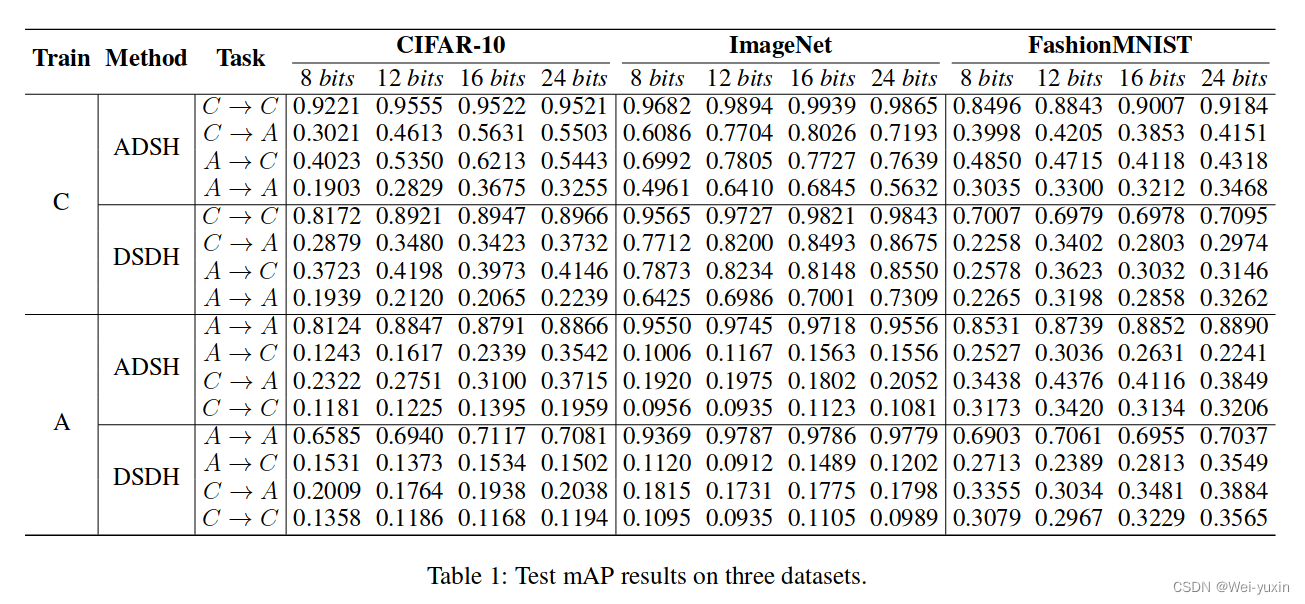
论文名称	Clean-label Backdoor Attack against Deep Hashing based Retrieval
作者	Kuofeng Gao （Tsinghua University）
出版社	arxiv 2021
pdf	在线pdf
代码	无

简介：本文提出了首个针对 hashing 模型的 clean-label backdoor attack。生成 targeted adversarial patch 作为 trigger，生成 confusing perturbations 去阻碍模型的学习，让其学到更多 trigger 信息。其中 confusing perturbations 是难以察觉的。作者通过实验验证了该方法的有效性，例如使用40张 poison data 就可以使攻击成功。

2.introduction

背景：

针对 hashing retrieval 的 clean-label backdoor attack

文章的贡献：

1. 提出了首个针对 hashing 系统的 clean-label backdoor attack
2. 提出了 confusing perturbations 的方法促使模型学到更多 trigger 信息
3. 验证了实验的效果 including transfer-based attack, less number of poisoned images

deep hashing：

$\mathbf{h}=F(\mathbf{x})=\mathrm{sign}\left(f_{\mathbf{\theta }}(\mathbf{x})\right)$

由于符号函数的梯度的梯度问题，可以使用 $tanh(.)$ 进行代替

$F^{\prime }(\mathbf{x})=\tanh \left(f_{\mathbf{\theta }}(\mathbf{x})\right)$

3.method

3.1 模型结构

算法的流程为：

1. 根据 target 类生成 universal adversarial patch 作为 trigger
2. 根据 target 类生成 confusing perturbations
3. 对数据进行投毒，生成带有 trigger 和 confusing perturbations 的数据集
4. 使用 posion 数据集训练 backdoor 模型
5. 测试 backdoor 模型的 map 和 t-map

3.2 Trigger Generation

论文在图片的左下角生成trigger：

injection function()​:

$\hat{\mathbf{x}}=B(\mathbf{x},\mathbf{p})=\mathbf{x}\odot (1-\mathbf{m})+\mathbf{p}\odot \mathbf{m}$

• $p$ trigger pattern
• $m$ predefined mask
• $\odot$ denotes the element-wise product
• 该公式参照了论文： (clean-label videos attack)

参考论文 DHTA 本文作者使用 DHTA 中生成 universal adversarial patch 的方法生成 trigger

${\min }_{\mathbf{p}}{\sum }_{\left({\mathbf{x}}_i,{\mathbf{y}}_i\right)\in \mathbf{D}}{d}_H\left(F^{\prime }\left(B\left({\mathbf{x}}_i,\mathbf{p}\right)\right),{\mathbf{h}}_a\right)$

• $D$: training set

• $h_a$ anchor code

  $h_a$ anchor code 是一串能代表 target 类的哈希码 （由 DHTA 提出）

  h a = arg ⁡ min ⁡ h ∈ { + 1 , − 1 } K ∑ ( x i , y i ) ∈ D ( t ) d H ( h , F ( x i ) ) \boldsymbol{h}_{a}=\arg \min _{\boldsymbol{h} \in\{+1,-1\}^{K}} \sum_{\left(\boldsymbol{x}_{i}, \boldsymbol{y}_{i}\right) \in \boldsymbol{D}^{(t)}} d_{H}\left(\boldsymbol{h}, F\left(\boldsymbol{x}_{i}\right)\right) ha​=argminh∈{+1,−1}K​∑(xi​,yi​)∈D(t)​dH​(h,F(xi​))

• $p$ trigger

通过优化该目标函数，生成的 trigger ，模型会将其判断为 target 类

所有 poison data 都共用同一个 trigger

3.3 Perturbing Hashing Code Learning

为了迫使模型更加关注 trigger ，本文提出了在 posion data 中加入 confusing perturbations

受到文章：(Yang et al. 2018) 的启发，作者发现这些 perturbations 可增大 original query image 之间的距离

如图所示，加入 perturbations 后，原本紧密的 yurt 类变得十分分散。

本文的作者通过在 target 类中加入 perturbations，使得模型在学习带有 trigger 的 target 类信息时，更多地学习到 trigger 信息

**目标函数：**​

L c ( { η i } i = 1 M ) = 1 M ( M − 1 ) ∑ i = 1 M ∑ j = 1 , j ≠ i M d H ( F ′ ( x i + η i ) , F ′ ( x j + η j ) ) \begin{aligned} & L_{c}\left(\left\{\boldsymbol{\eta}_{i}\right\}_{i=1}^{M}\right) \\=& \frac{1}{M(M-1)} \sum_{i=1}^{M} \sum_{j=1, j \neq i}^{M} d_{H}\left(F^{\prime}\left(\boldsymbol{x}_{i}+\boldsymbol{\eta}_{i}\right), F^{\prime}\left(\boldsymbol{x}_{j}+\boldsymbol{\eta}_{j}\right)\right) \end{aligned} =​Lc​({ηi​}i=1M​)M(M−1)1​i=1∑M​j=1,j​=i∑M​dH​(F′(xi​+ηi​),F′(xj​+ηj​))​

• $M$ 张 target 类的图片
• ${\mathbf{\eta }}_i$ 表示为 $x_i$ 的 perturbations
• 为了让 perturbations imperceptible，引入了 ${\ell }_{\infty }$ 进行限制

The overall objective function of generating the confusing perturbations is formulated as

max ⁡ { η i } i = 1 M λ ⋅ L c ( { η i } i M ) + ( 1 − λ ) ⋅ 1 M ∑ i = 1 M L a ( η i ) \max _{\left\{\boldsymbol{\eta}_{i}\right\}_{i=1}^{M}} \lambda \cdot L_{c}\left(\left\{\boldsymbol{\eta}_{i}\right\}_{i}^{M}\right)+(1-\lambda) \cdot \frac{1}{M} \sum_{i=1}^{M} L_{a}\left(\boldsymbol{\eta}_{i}\right) max{ηi​}i=1M​​λ⋅Lc​({ηi​}iM​)+(1−λ)⋅M1​∑i=1M​La​(ηi​)
s.t. ${\Vert {\mathbf{\eta }}_i\Vert }_{\infty }\le ϵ,i=1,2,\dots ,M$

• $L_a\left({\mathbf{\eta }}_i\right)=d_H\left(F^{\prime }\left({\mathbf{x}}_i+{\mathbf{\eta }}_i\right),F\left({\mathbf{x}}_i\right)\right)$

4.experiments

4.1 实验细节

数据集的划分：

Datasets and Target Models.

数据集	train	query	database	class
ImageNet	100*100（from database）	50*100	1300*100	100
MS-COCO	10000	5000	117218	80
Places365	9000	3600	36000	36

• ImageNet：数据集的划分方法按照 (hashnet-pdf)，数据集可由HashNet-github上下载
• MS-COCO：数据集的划分方式按照（hashnet-pdf），数据集可由HashNet-github上下载
• Places365：数据集的划分方式按照 (hashstash-pdf)，数据集可由 HashStash-github下载

target models

• hashing target models 的设置：使用预训练好的分类网络，进行 fine-tune 。再将分类网络最后一层换为 hashing layer 然后微调。

  • 具体网络结构有：

    • VGG-11，VGG-13
    • ResNet-34，ResNet-50，WideResNet-50-2：

    训练过程的具体描述在文章 Appendix B 中

• 除了最基本的 hashing 模型，文中还对 HashNet 和 DCH 进行了测试

Attack Settings

选择了5类作为target label

poisoned images is 60 on all datasets

• During the process of the trigger generation, we optimize the trigger pattern with the batch size 32 and the step size 12. The number of iterations is set as 2,000.
• Generating the confusing perturbations. The perturbation magnitude $\epsilon$ is set to 0.032. The number of epoch is 20 and the step size is 0.003. The batch size is set to 20 for generating the confusing perturbations.

对比实验的设置：

Tri：加入了trigger

Tri+Noise：加入了trigger和均匀分布的噪声

Tri+Adv：加入了 trigger 和 adversarial perturbations

4.2 评价指标

t-map：We calculate the t-MAP on top 1,000 retrieved images on all datasets.

4.3 实验

• Main Results

  证明了文中方法的有效性
  

• Attacking Advanced Hashing Methods

  分别对 HashNet 和 DCH 进行了实验的验证

• Resistance to Defense Methods

  验证攻击模型在面对防御时的效果

  1. Resistance to Spectral Signature Detection
  2. Resistance to Differential Privacy-based Defense
  3. Resistance to Pruning-based Defense

• Transfer-based Attack

  使用不同的模型（VGG，resnet）验证攻击方法的迁移能力

  两种实验设置：

  1. Ensemble：使用所有模型来生成 posion data
  2. Hold-out：使用除了目标模型之外的模型 生成 posion data

  从实验结果来看，迁移的能力并不强​

• Ablation Study

  证明每个函数的作用

• Less Visible Trigger

  作者在附录做的关于trigger的实验

  实验结果：

  

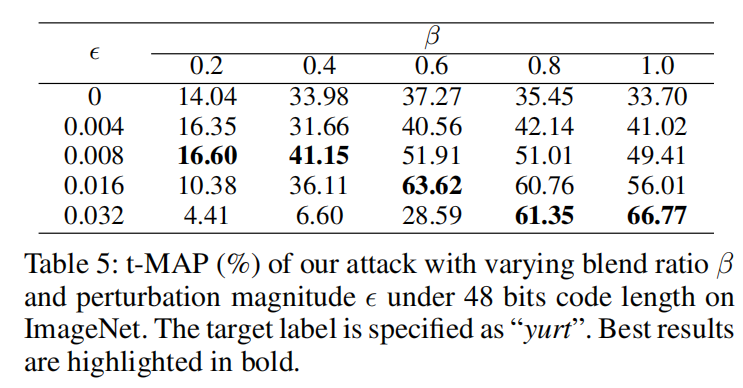
  其中$ϵ$为perturbation magnitude，$\beta$ 为trigger 的 blend ratio。$\beta$ 控制trigger的隐匿性，$\beta$ 值越小，trigger越隐秘。

  可以由实验看到，trigger的能见度越小，攻击的效率越差​