| 论文名称 | Proactive Privacy-preserving Learning for Retrieval |
|---|---|
| 作者 | Peng-Fei Zhang (University of Queensland) |
| 会议/出版社 | AAAI 2021 |
| 📄在线pdf | |
| 代码 | 无代码 |
-
概要:
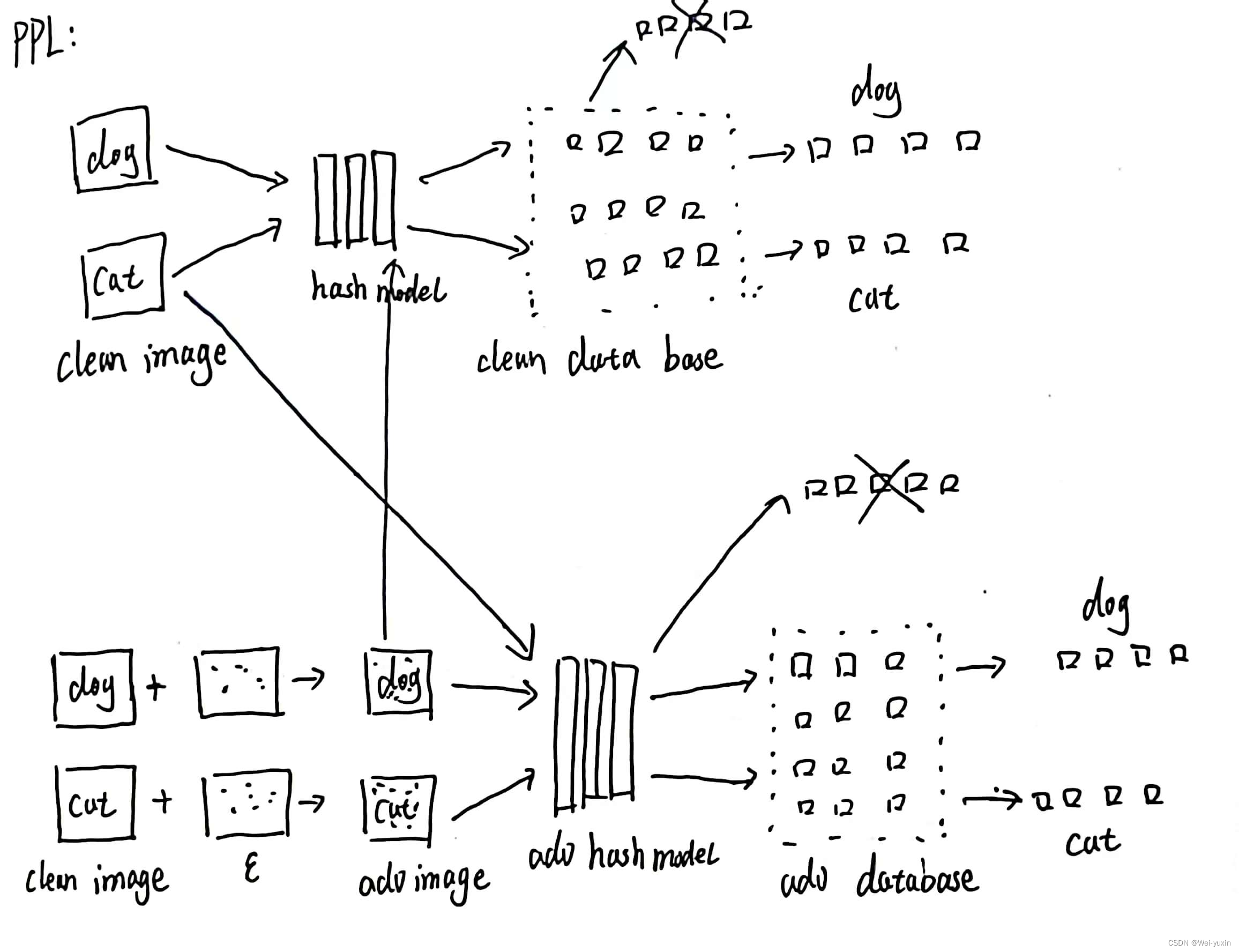
- 本文提出了一种针对检索系统隐私保护的方法,称为 PPL。训练一个生成器,在 original data 的基础上生成 adversarial data。adversarial data 在特征空间中要保持原本的相似性结构,并且最大化original data 和 adversarial data 之间的差距。
-
背景:
-
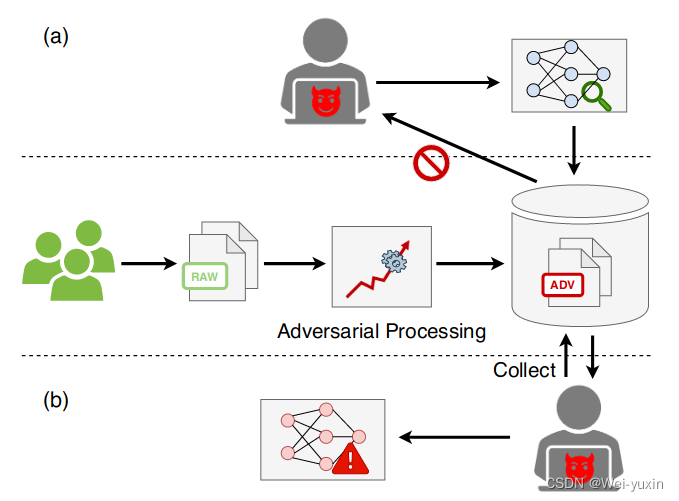
加入隐私保护后,恶意用户无法随意搜索,也无法收集 database 里的数据构建模型
-
具体来说就是:无法使用干净数据作为 query 在对抗性数据构建的 database 上进行检索,无法使用对抗性数据作为 query 在干净数据构建的 database 上进行检索
-
clean domain 和 adversarial domain 需要具有:
- 特征空间中相同的 similarity structure (pdf)
- 最大化两个领域之间的 gap
-
-
方法:
-
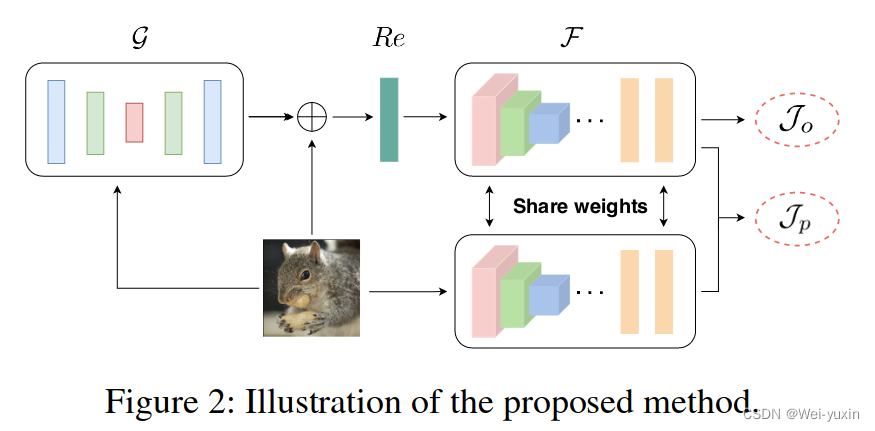
训练一个用于生成 adversarial data 的 generater
-
-
loss function
-
generation process
z i = x i + G ( x i ; ϑ g ) z_{i}=x_{i}+\mathcal{G}\left(x_{i} ; \vartheta_{g}\right) zi=xi+G(xi;ϑg)
s.t. ∥ G ( x i ; ϑ g ) ∥ p ≤ ϵ , p ∈ { 1 , 2 , ∞ } \left\|\mathcal{G}\left(x_{i} ; \vartheta_{g}\right)\right\|_{p} \leq \epsilon, p \in\{1,2, \infty\} ∥G(xi;ϑg)∥p≤ϵ,p∈{1,2,∞} -
Affinity-preserving Loss
- J o = ∑ i , j = 1 n ∥ h ( z i ) T h ( z j ) − c ⋅ S i j ∥ F 2 \mathcal{J}_{o}=\sum_{i, j=1}^{n}\left\|h\left(z_{i}\right)^{T} h\left(z_{j}\right)-c \cdot S_{i j}\right\|_{F}^{2} Jo=∑i,j=1n∥∥∥h(zi)Th(zj)−c⋅Sij∥∥∥F2
- 保持模型的检索能力额
-
Privacy-preserving Loss
J p = α D ^ s + β J s + γ J e \mathcal{J}_{p}=\alpha \widehat{\mathcal{D}}_{s}+\beta \mathcal{J}_{s}+\gamma \mathcal{J}_{e} Jp=αD s+βJs+γJe
- Domain Loss:原理涉及 “(RKHS)”
- Similarity Loss
- Matching Loss
具体细节阅读文章,loss 还有一些原理不太明白,不过该 loss 的主要目的是为了减小两个梁宇之间的差异
-
-
训练过程
-
Objective Function
这里的训练过程是一种对抗性训练方式,the generator is updated to enlarge the gap between the adversarial data and the original data,the surrogate model is trained with the opposing objective that is to maintain the search performance.
ϑ ^ g = arg min ϑ g J o ( ϑ g , ϑ f ) − J p ( ϑ g , ϑ f ) \hat{\vartheta}_{g}=\arg \min _{\vartheta_{g}} \mathcal{J}_{o}\left(\vartheta_{g}, \vartheta_{f}\right)-\mathcal{J}_{p}\left(\vartheta_{g}, \vartheta_{f}\right) ϑ^g=argminϑgJo(ϑg,ϑf)−Jp(ϑg,ϑf),
ϑ ^ f = arg min ϑ f J o ( ϑ g , ϑ f ) + J p ( ϑ g , ϑ f ) . \hat{\vartheta}_{f}=\arg \min _{\vartheta_{f}} \mathcal{J}_{o}\left(\vartheta_{g}, \vartheta_{f}\right)+\mathcal{J}_{p}\left(\vartheta_{g}, \vartheta_{f}\right) . ϑ^f=argminϑfJo(ϑg,ϑf)+Jp(ϑg,ϑf). -
对抗性训练的过程运用到了 Gradient Reversal Layer
-
来自论文-Unsupervised Domain Adaptation by Backpropagation 是关于 domain adaptation 的文章
-
-
-
-
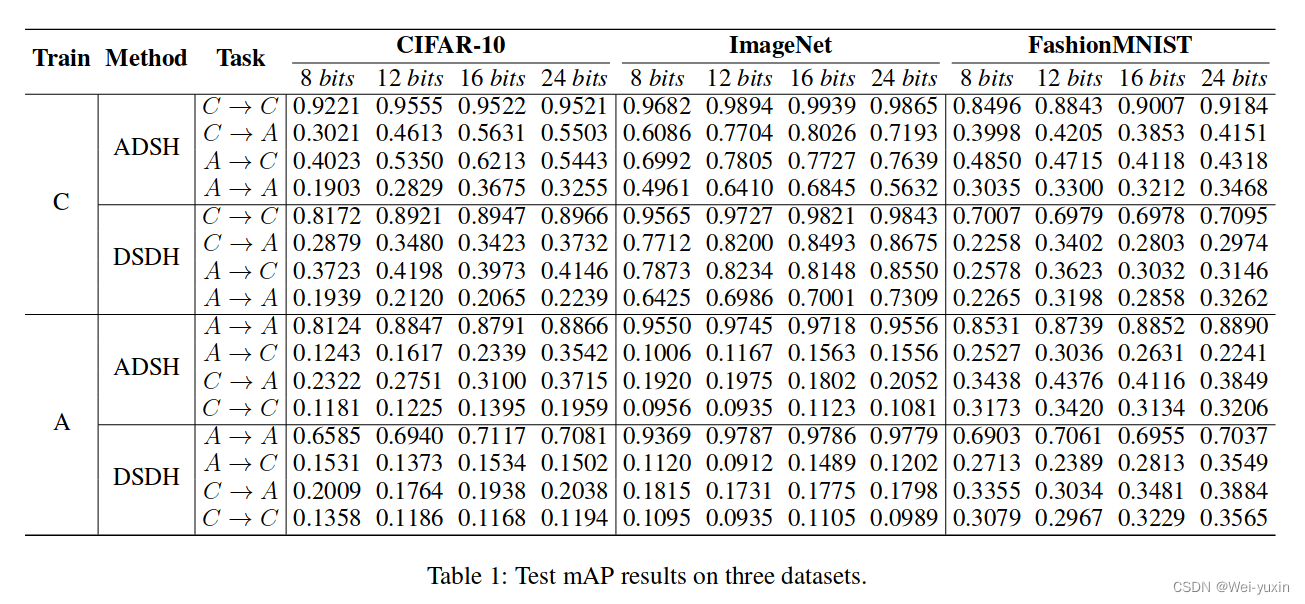
实验结果: