(必经点)局部优化达到全局最优的最短路径算法探讨

news2024/11/9 6:08:18

首先，存在无序的点集 $D=\left \{ p_{1},p_{2},p_{3},...,p_{n} \right \},n\epsilon \mathbb{N}^{+}$ .

记 $D[0]=p_{1},D[1]=p_{2},...,D[n-1]=p_{n}$ .

再记初始路径为 $C=s{D[0],D[1],D[2],...,D[n]}e$ .

于是，我们称以下为一次变换 $T$ ：

if |C[i]-C[i+1]|+|C[i+2]-C[i+3]| > |C[i]-C[i+2]|+|C[i+1]-C[i+3]|
{
    swap(C[i+1],C[i+2]);
}

需要注意的是 $C[0]=s,C[C.size-1]=e$ .

最直观的就是如下的变换：

我们对C上的每一点，依次进行如上的变换，不断的循环，直至不再需要变换，此时的路径C就是最短路径。因为每次变换后，C上的点只是两个点之间交换了顺序，而其他的点不变，同时，变换后的路径，又能保证比变换前的短，所以我们可以断定此种方法是收敛的。而且最终会达到极小值，而此时，再对C上的每一次做T，都不会进入到上述的if里面。

现在，我们来初步的看看此种方式的最大复杂度。

我们将初始路径作个变形：

若我们从 $s$ 到 $e$ ,依次作 $T$ 变换。最开始，若每次 $T$ 都会 $swap$ 一次，则在链上，每次 $T$ 变换后， $p_{1}$ 都会顺时针移动一位。我们称 $C.size-3$ 次 $T$ 为一次循环。每次循环后，必定会有一个点挪到末端。若假设其中有 $C.size-3$ 个点需要做变换，那么就会有 $C.size-3$ 次循环，每次循环有 $C.size-3$ 次变换。这是最大的计算复杂度。

另外，我们需要关注到的是，每经过一次循环后，每个路径上，都会将离的近的点拉进，离得远的点推远。靠近s端的点会变得靠s端，靠近e端的会变得靠e端。

基于这样的一个现象，如果我们在初始化路径的时候，能自动的，将互相靠近的点相连接，那么，将会大大缩短循环的次数。

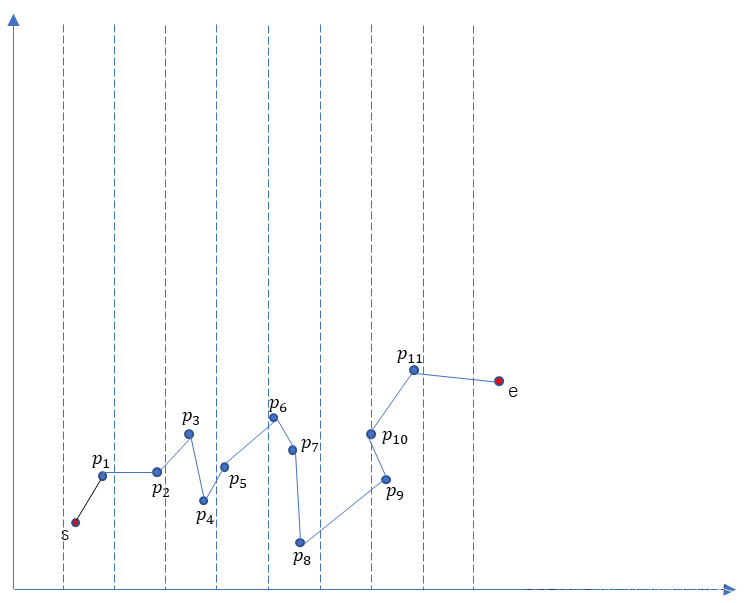
在这里提出一种方式，我们将坐标平面沿X轴，以 $d$ 的间隔进行分割，来进行初始化路径。具体的伪代码形式：

点集:D={P1,P2,P3,...,Pn}
二维数组:A[][];

int d=10;//栅格间距
int max_i=0;//最大的区间数
for i=0;i<D.size();i++
{
    A[D[i].x/d].push_back(D[i]);
    if D[i].x/d > max_i
        max_i=D[i].x/d;
}

设路径序列C={}

则我们生成路径
for n=0;n<max_i;n++
{
    for t=0;t<A[n].size;t++
    {
        C.push_back(A[n][t]);
    }
}

C.insert(s) at 0;
C.push_back(e);

最后，我们开始逐项局部优化
bool is_changed=false;
Optimize:
    for i=0;i<C.size-3;i++
    {
        if |C[i]-C[i+1]|+|C[i+2]-C[i+3]| > |C[i]-C[i+2]|+|C[i+1]-C[i+3]|
        {
            exchange(C[i+1],C[i+2]);
            is_changed=true;
        }
    }

if is_changed
    go back to Optimize;
else
{
    if |C[0]-C[1]|+|C[C.size-1]-C[C.size-2]| > |C[0]-C[C.size-2]|+|C[C.size-1]-C[0]|
        exchange(C[0],C[C.size-1]);
}

此算法只是初步设想，具体的算法运行效率，后续会做试验进行验证。有什么不对之处，望指教出来，谢谢！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/23511.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！