流水线记忆要点‌

题目：

流水线技术中，若某流水线分为5段，每段执行时间为Δt，则执行100条指令的总时间为（ ）
A. 100Δt
B. 104Δt
C. 500Δt
D. 505Δt
答案：B‌
‌解析：流水线总时间=(n+k-1)Δt，n=100，k=5。

问题解析与答案

在流水线技术中，若某流水线分为5段（k=5），每段执行时间为Δt，执行100条指令（n=100）的总时间计算公式为：

总时间 = (n + k - 1) × Δt
代入数值：
总时间 = (100 + 5 - 1) × Δt = 104Δt
因此正确答案为 B. 104Δt (#user-content-evidence-12)(#user-content-evidence-13)(#user-content-evidence-21)。

---

流水线技术核心知识点整理

1. 流水线周期

• 定义：流水线中最慢阶段的执行时间称为流水线周期。若各段执行时间相等（均为Δt），则周期为Δt (#user-content-evidence-3)(#user-content-evidence-12)。
• 关键公式：

  

---

2. 流水线总时间计算

• 公式：

  

• 推导逻辑：

  

---

3. 吞吐率（Throughput, TP）

• 定义：单位时间内完成的指令数量。

• 公式：

  

---

4. 加速比（Speedup, S）

• 定义：使用流水线后效率提升的倍数。

• 公式：

  

---

5. 效率（Efficiency, E）

• 定义：流水线设备的利用率，时空图中被有效利用的区域占比。

• 公式（各段时间相等时）：

  

---

记忆卡片模板

---

流水线技术面临的挑战

1. 资源冲突：多指令争用同一硬件资源（如总线），需通过哈佛结构或插入气泡解决 (#user-content-evidence-1)。
2. 数据冲突：后续指令依赖前指令结果，可通过定向推送（数据旁路）或编译器优化缓解 (#user-content-evidence-1)。
3. 控制冲突：分支指令导致流水线断流，需动态分支预测或延迟槽技术 (#user-content-evidence-1)(#user-content-evidence-4)。

---

扩展思考

• 流水线深度优化：增加段数（k）可提高吞吐率，但会引入更复杂的硬件和更高的分支误预测惩罚 (#user-content-evidence-28)。
• 时空图分析：通过可视化时空区占比，直观评估效率与性能瓶颈 (#user-content-evidence-37)(#user-content-evidence-42)。

流水线技术多维度练习题集

（结合知识点设计多题型，包含计算、分析、应用、推导等，覆盖总时间、吞吐率、加速比、效率、冲突处理、时空图等核心内容）

题型一：基础计算题

题目1某流水线分为4段，各段执行时间均为2Δt。若需要执行50条指令，求：

1. 流水线周期
2. 总执行时间
3. 吞吐率
4. 加速比
5. 效率

解析与答案

1. 流水线周期 = 最长段执行时间 = 2Δt 
2. 总时间 = (k + n -1)Δt = (4 + 50 -1)×2Δt = 106Δt
3. 吞吐率 TP = 50 / 106Δt ≈ 0.472/Δt
4. 加速比 S = 顺序时间（50×4×2Δt） / 流水线时间（106Δt）= 400Δt / 106Δt ≈ 3.77
5. 效率 E = n / (k + n -1) = 50 / 53 ≈ 94.34%

题型二：选择题（多知识点综合）

题目2某指令流水线包含5段，各段时间分别为3Δt、2Δt、4Δt、2Δt、3Δt。执行80条指令时，流水线的吞吐率是（ ）A. 80/(5×4Δt)B. 80/(84Δt)C. 1/4ΔtD. 80/(80+5-1)×4Δt

解析与答案

1. 流水线周期为最长段4Δt，总时间 = (5 + 80 -1)×4Δt = 84×4Δt = 336Δt
2. 吞吐率 = 80 / 336Δt = 80/(336Δt) ，但选项B的分母未包含周期，需注意单位。
3. 正确公式应为 TP = n / [(k + n -1)×周期] ，即 80/(84×4Δt) ，但选项B写为80/(84Δt)，存在陷阱。
4. 正确答案：B（若题目忽略单位）或重新审题后选B 

题型三：应用题（多功能流水线）

题目3某动态多功能流水线由5段组成，加法使用段1、3、5（各段时间为2Δt），乘法使用段1、2、4、5（段4时间为3Δt）。现需计算表达式：

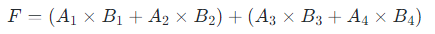
要求：

1. 设计流水线调度算法，避免数据冲突。
2. 画出时空图。
3. 计算实际吞吐率、加速比和效率。

解析与答案

1. 算法设计：

1. 先并行计算4次乘法：M1=A1×B1, M2=A2×B2, M3=A3×B3, M4=A4×B4
2. 再计算两次加法：A1=M1+M2, A2=M3+M4
3. 最后计算总和：F=A1+A2（需插入气泡避免段冲突）

1. 时空图关键点：

1. 乘法占用段1、2、4、5（段4为瓶颈，3Δt）
2. 加法占用段1、3、5（段1需等待乘法释放）

1. 性能计算：

1. 总时间：假设调度后需20Δt（具体依赖时空图）
2. 吞吐率 TP = 7结果 / 20Δt （最终输出1个F，但中间结果7个）
3. 加速比 S = 顺序时间（4×乘法时间 + 3×加法时间） / 20Δt乘法时间=1+2+4+5=12Δt，加法时间=1+3+5=9Δt → 顺序时间=4×12 + 3×9 = 75Δt → S=75/20=3.75
4. 效率 E = (有效时空区) / (总时空区) ≈ 60%

题型四：冲突分析题

题目4某5段流水线（取指IF、译码ID、执行EX、访存MEM、写回WB）执行以下指令序列：

 分析指令2与指令1之间的冲突类型，并提出两种解决方案。

解析与答案

1. 冲突类型：指令2的EX段需要R1，但指令1在WB段才写回R1 → 数据冲突（RAW） 
2. 解决方案：

1. 转发技术（Data Forwarding） ：将指令1的EX段结果直接转发给指令2的EX段。
2. 插入气泡：延迟指令2的执行，直到指令1完成WB。

题型五：时空图绘图题

题目5某3段流水线（S1:1Δt, S2:2Δt, S3:1Δt）处理4个任务。要求：

1. 画出时空图，标出各任务占用段的时间。
2. 计算吞吐率和效率。

解析与答案

题型六：公式推导题

题目6

 

推导过程

1. 定义：效率 = 有效时空区 / 总时空区
2. 有效时空区：n个任务占用k段 → n×k×Δt
3. 总时空区：k段 × 总时间 = k × (k + n -1)Δt
4. 公式：

（注：实际推导中需考虑段数与时序，此简化版本适用于均匀流水线）

题型七：综合应用题（参数影响分析）

题目7某流水线原设计为5段，现将其改造为8段，每段执行时间缩短为原周期的0.6倍（原周期为T）。

1. 若处理n条指令，分析改造后的加速比变化。
2. 讨论段数增加可能带来的问题。

解析与答案

1. 加速比分析：

1. 原总时间 = (5 + n -1)T = (n +4)T
2. 新周期 = 0.6T，总时间 = (8 + n -1)×0.6T = (n +7)×0.6T
3. 加速比变化：

• 当n→∞时，极限为5/8 → 加速比下降

1. 问题：

1. 流水线深度增加导致分支误预测惩罚增大。
2. 段间缓冲和冲突管理复杂度上升。
3. 资源冲突概率增加（如寄存器端口争用）