🔥 本文由 程序喵正在路上 原创,CSDN首发!
💖 系列专栏:数据结构与算法
🌠 首发时间:2022年11月21日
🦋 欢迎关注🖱点赞👍收藏🌟留言🐾
🌟 一以贯之的努力 不得懈怠的人生
阅读指南
- 最小生成树
- 生成树
- 最小生成树(最小代价树)
- Prim 算法(普利姆)
- Kruskal 算法(克鲁斯卡尔)
- 最短路径
- BFS 求无权图的单源最短路径
- Dijkstra 算法
- Floyd 算法
- 总结
最小生成树
生成树
连通图的生成树是包含图中全部顶点的一个极小连通子图(边尽可能少,但要保持连通)
若图中顶点数为 n n n,则它的生成树有 n − 1 n - 1 n−1 条边。对生成树而言,若砍去它的一条边,则会变成非连通图,若加上一条边则会形成一个回路
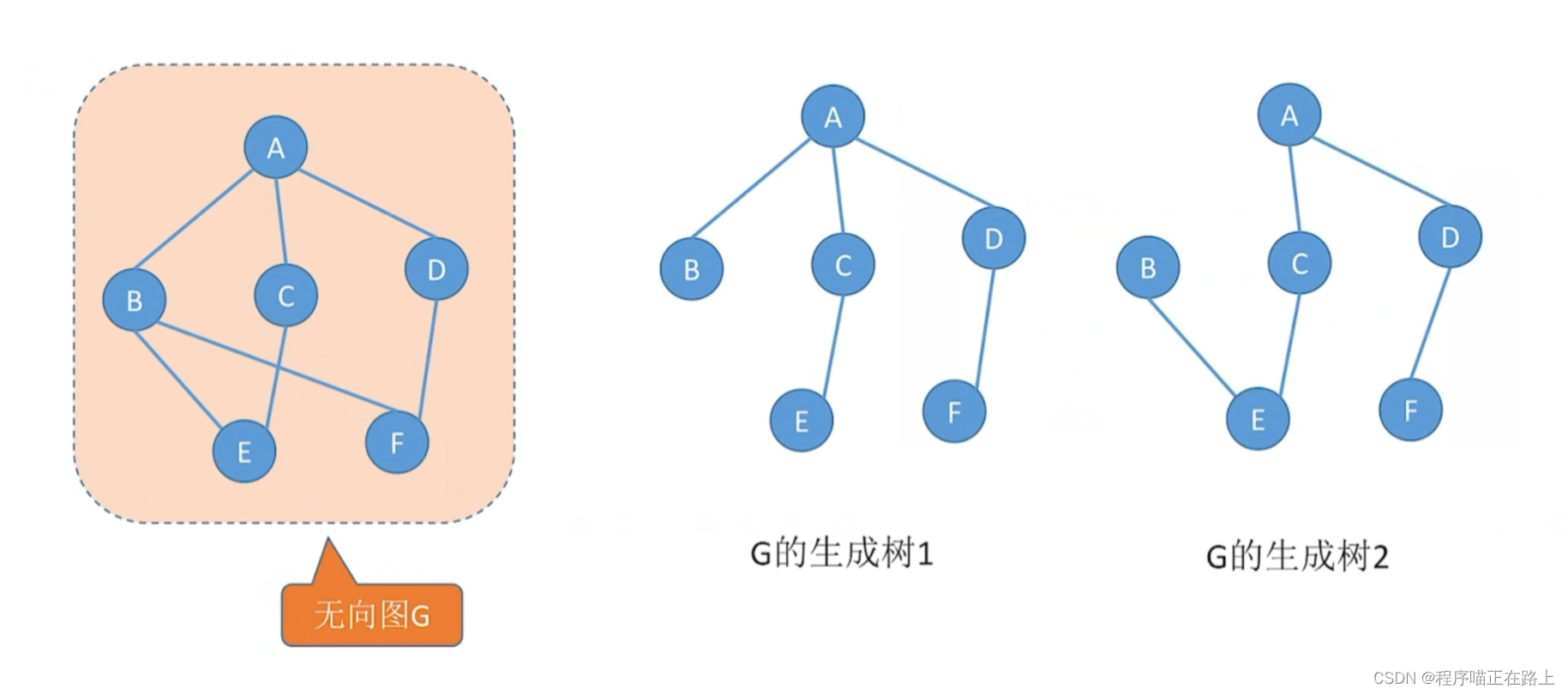
最小生成树(最小代价树)
我们来看一个问题:有下图这么几个地方构成的图,图中每条边上的数字是修路的费用,然后要我们规划道路,让所有地方都连通,并且成本要尽可能低
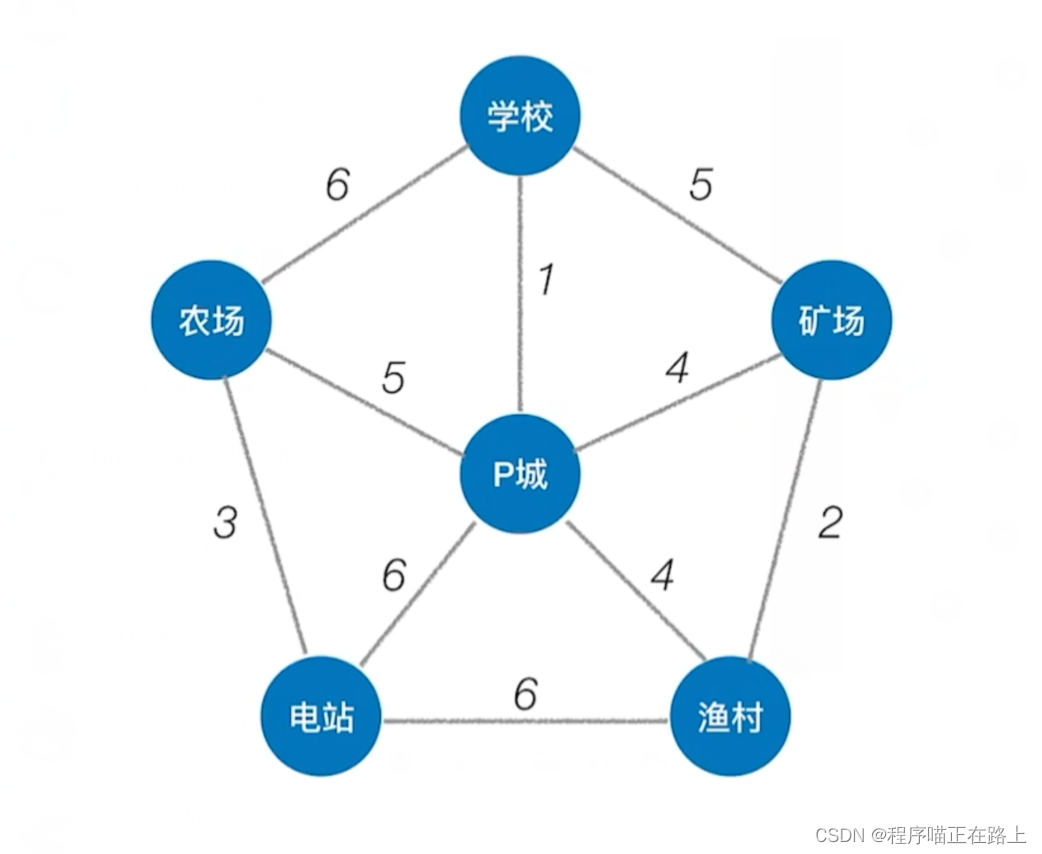
其实要我们找的,就是这个图的最小生成树
对于一个带权连通无向图 G = ( V , E ) G = (V, E) G=(V,E),生成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设 R R R 为 G G G 的所哟生成树的集合,若 T T T 为 R R R 中边的权值之和最小的生成树,则 T T T 称为 G G G 的最小生成树( M i n i m u m − S p a n n i n g − T r e e , M S T Minimum-Spanning-Tree, MST Minimum−Spanning−Tree,MST)
注意:
- 最小生成树可能有多个,但边的权值之和总是唯一且最小的
- 最小生成树的边数等于顶点数 − 1 - 1 −1,删掉一条边则不连通,增加一条边则会出现回路
- 如果一个连通图本身就是一棵树,则其最小生成树就是它本身
- 只有连通图才有生成树,非连通图只有生成森林
Prim 算法(普利姆)
从某一个顶点开始构建生成树,每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止
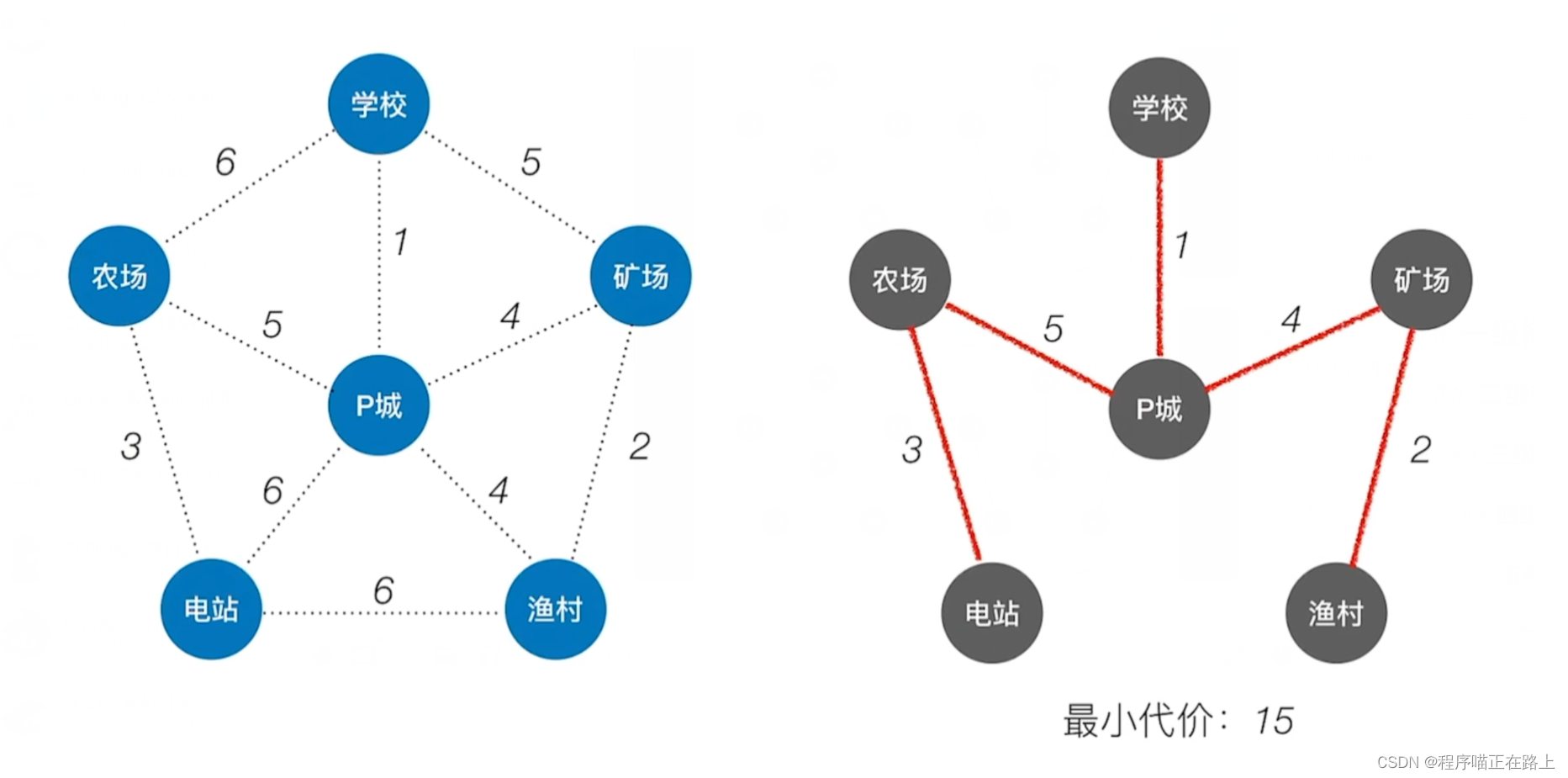
时间复杂度为 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2),适合用于边稠密图
Kruskal 算法(克鲁斯卡尔)
每次选择一条权值最小的边,使这条边的两头连通(原本已经连通的就不选),直到所有结点都连通
时间复杂度为 O ( ∣ E ∣ l o g 2 ∣ E ∣ ) O(|E|log_2|E|) O(∣E∣log2∣E∣),适合用于边稀疏图
最短路径
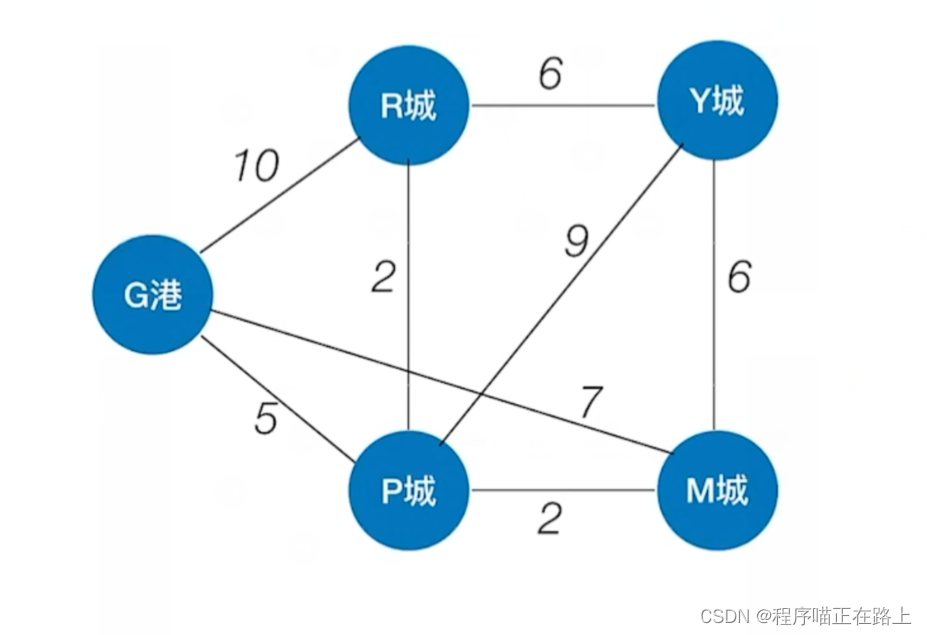
“G港” 是个物流集散中心,经常需要往各个城市运送东西,怎么运送距离最近? —— 单源最短路径问题
各个城市之间也需要互相往来,相互之间怎么走距离最近? —— 每对顶点间的最短路径
BFS 求无权图的单源最短路径
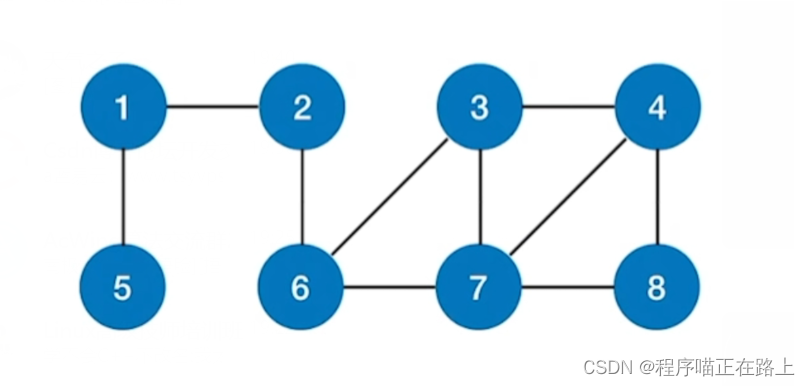
无权图可以视为一种特殊的带权图,只是每条边的权值都为 1 1 1
我们对广度优先遍历的代码稍微改改,就能得到最短路径的 B F S BFS BFS 算法
//求顶点 u 到其他顶点的最短路径
void BFS_MIN_Distance(Graph G, int u) {
//d[i] 表示从 u 到 i 结点的最短路径
for (int i = 0; i < G.vexnum; ++i) {
d[i] = 0; //初始化最短路径长度
path[i] = -1; //最短路径是从哪个顶点过来的
}
d[u] = 0;
visited[u] = true;
EnQueue(Q, u);
while (!isEmpty(Q)) { //BFS算法主过程
DeQueue(Q, u); //队头元素 u 出队
for (w = FirstNeighbor(G, u); w >= 0; w = NextNeighbor(G, u, w)) {
if (!visited[w]) { //w 为 u 的尚未访问的邻接顶点
d[w] = d[u] + 1; //路径长度加 1
path[w] = u; //最短路径为从 u 到 w
visited[w] = true; //设置已访问标记
EnQueue(Q, w); //顶点 w 入队
}//if
}//for
}//while
}
如果我们从 2 2 2 这个顶点对图进行广度优先遍历,那么得到的广度优先生成树一定是以 2 2 2 为根的、高度最小的生成树
B F S BFS BFS 算法的局限性 —— 求单源最短路径只适用于无权图,或者所有边的权值都相同的图
Dijkstra 算法
带权路径长度 —— 当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度
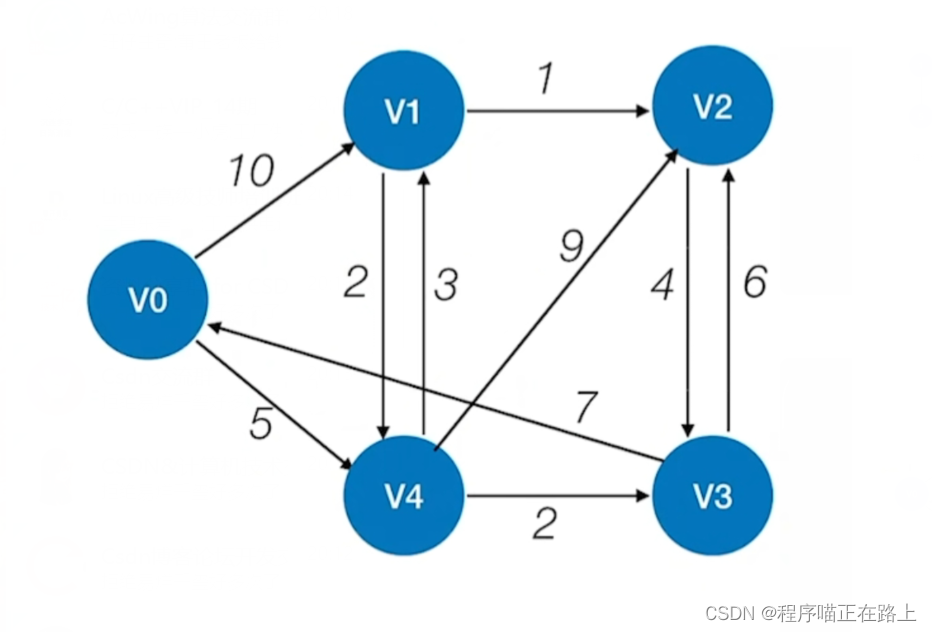
我们需要 3 3 3 个数组:
- f i n a l final final 数组:标记各顶点是否已经找到最短路径
- d i s t dist dist 数组:顶点的最短路径长度
- p a t h path path 数组:路径上的前驱顶点
初始:若从 V 0 V_0 V0 开始,令 f i n a l [ 0 ] = t r u e ; d i s t [ 0 ] = 0 ; p a t h [ 0 ] = − 1 final[0] = true; dist[0] = 0; path[0] = -1 final[0]=true;dist[0]=0;path[0]=−1,其余顶点 f i n a l [ k ] = f a l s e ; d i s t [ k ] = a r c s [ 0 ] [ k ] ; p a t h [ k ] = ( a r c s [ 0 ] [ k ] = = ∞ ) ? − 1 : 0 final[k] = false; dist[k] = arcs[0][k]; path[k] = (arcs[0][k] == \infty) \ ? -1 : 0 final[k]=false;dist[k]=arcs[0][k];path[k]=(arcs[0][k]==∞) ?−1:0
后面的 n − 1 n - 1 n−1 轮处理:循环遍历所有顶点,找到还没有确定最短路径,且 d i s t dist dist 最小的顶点 V i V_i Vi, 令 f i n a l [ i ] = t r u e final[i] = true final[i]=true。并检查所有邻接自 V i V_i Vi 的顶点 V j V_j Vj,若 f i n a l [ j ] = f a l s e final[j] = false final[j]=false 且 d i s t [ i ] + a r c s [ i ] [ j ] < d i s t [ j ] dist[i] + arcs[i][j] < dist[j] dist[i]+arcs[i][j]<dist[j],则令 d i s t [ j ] = d i s t [ i ] + a r c s [ i ] [ j ] ; p a t h [ j ] = i dist[j] = dist[i] + arcs[i][j]; \ path[j] = i dist[j]=dist[i]+arcs[i][j]; path[j]=i( a r c s [ i ] [ j ] arcs[i][j] arcs[i][j] 表示 V i V_i Vi 到 V j V_j Vj 的弧的权值)
时间复杂度为 O ( N 2 − N ) O(N^2 - N) O(N2−N),简化后为 O ( N 2 ) O(N^2) O(N2)(其中 N N N 为顶点个数),在这个过程中,每一轮处理我们都需要循环遍历所有顶点,找到还没有确定最短路径,且 d i s t dist dist 最小的顶点 V i V_i Vi,这一步需要 O ( N ) O(N) O(N) 的时间,因为有 N N N 个点,然后有 n − 1 n - 1 n−1 处理,相乘即为此算法的时间复杂度
注意:Dijkstra 算法不适用于有负权值的带权图
Floyd 算法
F l o y d Floyd Floyd 算法:求出每一对顶点之间的最短路径
使用动态规划思想,将问题的求解分为多个阶段
对于 n n n 个顶点的图 G G G,求任意一对顶点 V i V_i Vi -> V j V_j Vj 之间的最短路径可分为如下几个阶段:
- 初始:不允许在其他顶点中转,最短路径是?
- 0:若允许在 V 0 V_0 V0 中转,最短路径是?
- 1:若允许在 V 0 、 V 1 V_0、V_1 V0、V1 中转,最短路径是?
- 2:若允许在 V 0 、 V 1 、 V 2 V_0、V_1、V_2 V0、V1、V2 中转,最短路径是?
- …
- n - 1:若允许在 V 0 、 V 1 、 V 2 、 . . . 、 V n − 1 V_0、V_1、V_2、... 、V_{n- 1} V0、V1、V2、...、Vn−1 中转,最短路径是?
假设有如下这个图,要我们求出每一对顶点之间的最短路径
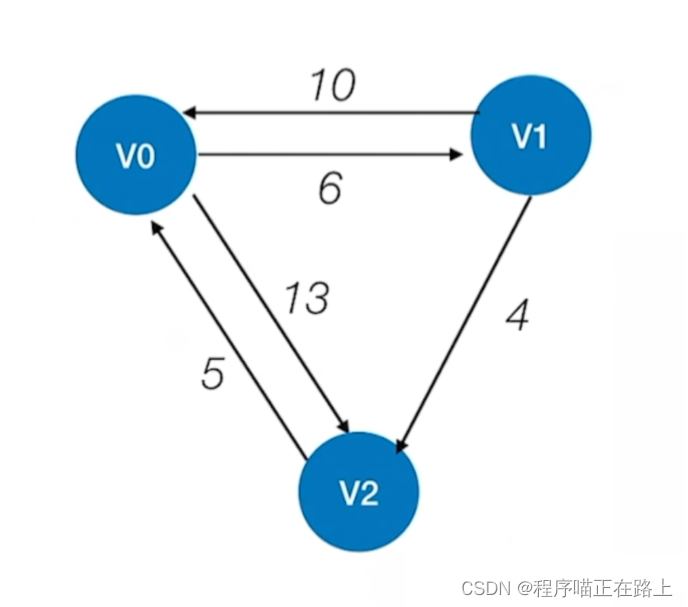
我们一步步来分析这个问题
初始状态,不允许在其他顶点中转,其最短路径(也就是图的邻接矩阵)为

每两个顶点之间的中转点为( − 1 -1 −1 表示无中转点)
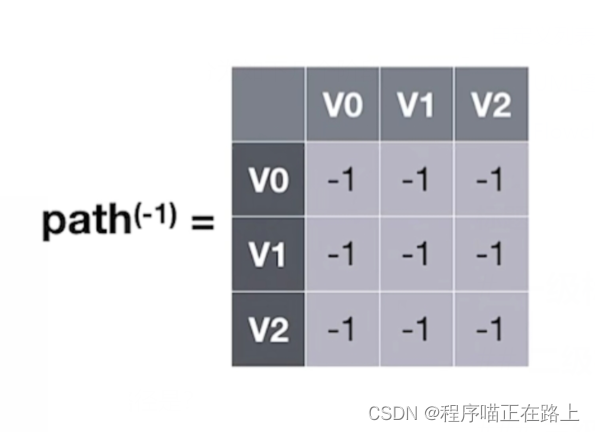
接着,下一步,若允许在 V 0 V_0 V0 中转,最短路径是什么呢?
对此,我们需要进行下列比较:
- 若 A ( k − 1 ) [ i ] [ j ] > A ( k − 1 ) [ i ] [ k ] + A ( k − 1 ) [ k ] [ j ] A^{(k-1)}[i][j] > A^{(k-1)}[i][k] + A^{(k-1)}[k][j] A(k−1)[i][j]>A(k−1)[i][k]+A(k−1)[k][j],则 A ( k ) [ i ] [ j ] = A ( k − 1 ) [ i ] [ k ] + A ( k − 1 ) [ k ] [ j ] ; A^{(k)}[i][j] = A^{(k-1)}[i][k] + A^{(k-1)}[k][j]; A(k)[i][j]=A(k−1)[i][k]+A(k−1)[k][j]; p a t h ( k ) [ i ] [ j ] = k \ path^{(k)}[i][j] = k path(k)[i][j]=k,否则, A ( k ) A^{(k)} A(k) 和 A ( k − 1 ) A^{(k - 1)} A(k−1) 保持原值
在前面的 A ( − 1 ) A^{(-1)} A(−1) 图中,只有求 V 2 V_2 V2 到 V 1 V_1 V1 的最短路径时符合比较的要求:
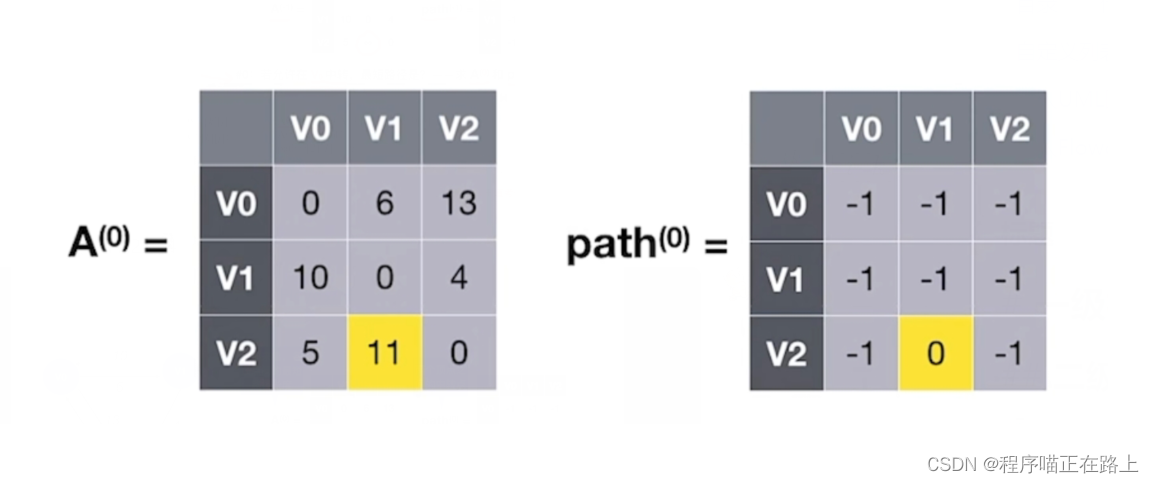
- A ( − 1 ) [ 2 ] [ 1 ] > A ( − 1 ) [ 2 ] [ 0 ] + A ( − 1 ) [ 0 ] [ 1 ] = 11 A^{(-1)}[2][1] > A^{(-1)}[2][0] + A^{(-1)}[0][1] = 11 A(−1)[2][1]>A(−1)[2][0]+A(−1)[0][1]=11
- 所以 A ( 0 ) [ 2 ] [ 1 ] = 11 , p a t h ( 0 ) [ 2 ] [ 1 ] = 0 A^{(0)}[2][1] = 11, \ path^{(0)}[2][1] = 0 A(0)[2][1]=11, path(0)[2][1]=0
对应的最短路径和中转点图为:
第 3 3 3 步,若允许在 V 0 、 V 1 V_0、V_1 V0、V1 中转,最短路径是?
在这一步,只有求 V 0 V_0 V0 到 V 2 V_2 V2 的最短路径时符合比较的要求:
- A ( 0 ) [ 0 ] [ 2 ] > A ( 0 ) [ 0 ] [ 1 ] + A ( 0 ) [ 1 ] [ 2 ] = 10 A^{(0)}[0][2] > A^{(0)}[0][1] + A^{(0)}[1][2] = 10 A(0)[0][2]>A(0)[0][1]+A(0)[1][2]=10
- 所以 A ( 1 ) [ 0 ] [ 2 ] = 10 , p a t h ( 1 ) [ 0 ] [ 2 ] = 1 A^{(1)}[0][2] = 10, \ path^{(1)}[0][2] = 1 A(1)[0][2]=10, path(1)[0][2]=1
对应的最短路径和中转点图为:

第 4 4 4 步,若允许在 V 0 、 V 1 、 V 2 V_0、V_1、V_2 V0、V1、V2 中转,最短路径是?
在这一步,只有求 V 1 V_1 V1 到 V 0 V_0 V0 的最短路径时符合比较的要求:
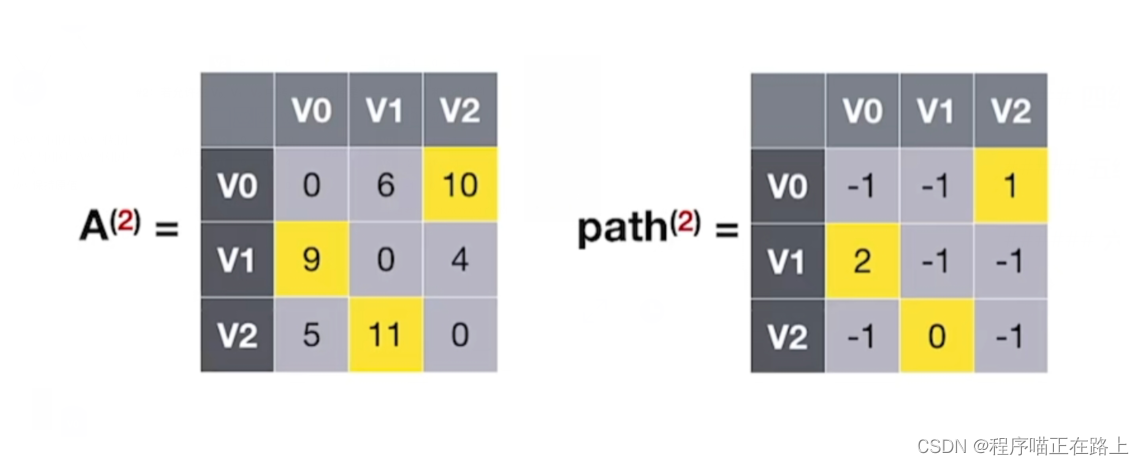
- A ( 1 ) [ 1 ] [ 0 ] > A ( 1 ) [ 1 ] [ 2 ] + A ( 1 ) [ 2 ] [ 0 ] = 9 A^{(1)}[1][0] > A^{(1)}[1][2] + A^{(1)}[2][0] = 9 A(1)[1][0]>A(1)[1][2]+A(1)[2][0]=9
- 所以 A ( 2 ) [ 1 ] [ 0 ] = 9 , p a t h ( 2 ) [ 1 ] [ 0 ] = 2 A^{(2)}[1][0] = 9, \ path^{(2)}[1][0] = 2 A(2)[1][0]=9, path(2)[1][0]=2
对应的最短路径和中转点图为:
从 A ( − 1 ) A^{(-1)} A(−1) 和 p a t h ( − 1 ) path^{(-1)} path(−1) 开始,经过 n n n 轮递推( n n n 为顶点个数),得到了 A ( n − 1 ) A^{(n-1)} A(n−1) 和 p a t h ( n − 1 ) path^{(n-1)} path(n−1)
核心代码如下
//前期准备工作,根据图的信息初始化矩阵 A 和 path
//每一步比较
for (int k = 0; k < n; ++k) { //考虑以 Vk 为中转点
for (int i = 0; i < n; ++i) { //遍历整个矩阵,i 为行号,j 为列号
for (int j = 0; j < n; ++j) {
if (A[i][j] > A[i][k] + A[k][j]) {
A[i][j] = A[i][k] + A[k][j]; //更新最短路径长度
path[i][j] = k; //更新中转点
}
}
}
}
时间复杂度为 O ( ∣ V ∣ 3 ) O(|V|^3) O(∣V∣3),空间复杂度为 O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2)
注意:
- F l o y d Floyd Floyd 算法可以用于负权值带权图
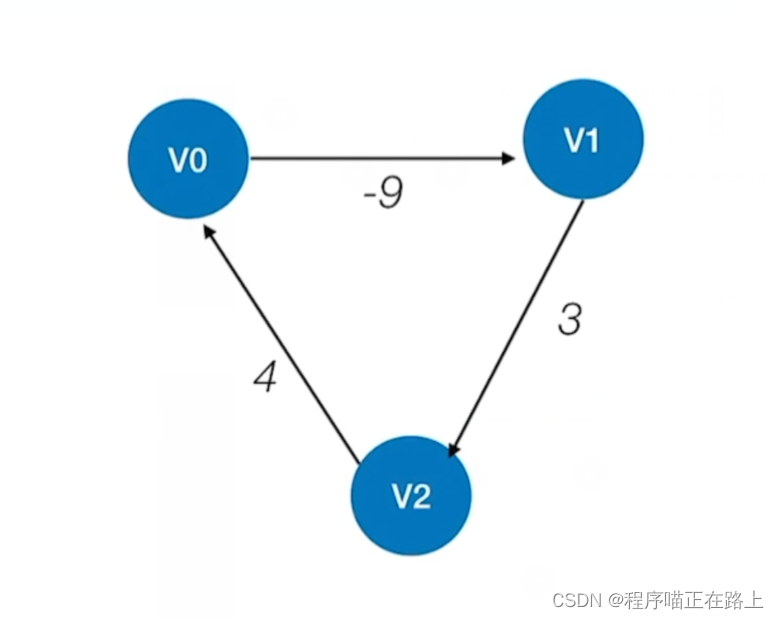
- F l o y d Floyd Floyd 算法不能解决带有 “负权回路” 的图(有负权值的边组成回路),这种图有可能没有最短路径,如下图
总结
| 对比方面 | BFS 算法 | Dijkstra 算法 | Floyd 算法 |
|---|---|---|---|
| 无权图 | ✔ | ✔ | ✔ |
| 带权图 | ✖ | ✔ | ✔ |
| 带负权值的图 | ✖ | ✖ | ✔ |
| 带负权回路的图 | ✖ | ✖ | ✖ |
| 时间复杂度 | O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2) 或 O ( ∣ V ∣ + ∣ E ∣ ) O(|V| + |E|) O(∣V∣+∣E∣) | O ( ∣ V ∣ 2 ) O(|V|^2) O(∣V∣2) | O ( ∣ V ∣ 3 ) O(|V|^3) O(∣V∣3) |
| 通常用于 | 求无权图的单源在最短路径 | 求带权图的单源最短路径 | 求带权图中各顶点间的最短路径 |
也可以用 D i j k s t r a Dijkstra Dijkstra 算法求所有顶点间的最短路径,重复 ∣ V ∣ |V| ∣V∣ 次即可,总的时间复杂度也为 O ( ∣ V ∣ 3 ) O(|V|^3) O(∣V∣3)











![[附源码]java毕业设计校园共享单车系统](https://img-blog.csdnimg.cn/619f8aedbe5a404fa73cf6f37bb50e6b.png)