连续时间信号的时域分析法
- 一、LTI 连续系统的响应
- 1. LTI 微分方程的建立与求解
- 2. LTI 连续系统的零输入响应与零状态响应
- 1. 零输入响应
- 2. 零状态响应
- 3. 全响应
- 二、冲激响应和阶跃响应
- 1. 冲激响应
- 2. 阶跃响应
- 三、卷积积分及其性质
- 1. 任意信号的分解
- 2. 任意信号作用下的零状态响应
- 3. 卷积的定义
- 4. 卷积性质
- 1. 代数性质
- 2. f(t)与奇异信号的卷积 (非常重要)
- 3. 卷积的微分和积分
- 4. 卷积时移
- 5. 常用信号的卷积公式
- 四、总结重点
在连续信号与系统实际计算时,如何分析和计算是最重要的,在实际计算时,基本上都是采用的是频域或者复频域计算的,最后的结果通过一系列转换得到时域的结果,所以,时域分析的话我们主要是要知道,时域求解时,系统的一些响应,了解一些时域的概念。真正实际使用时,时域直接分析法用的非常少,就是因为时域分析很麻烦。
下面的响应都是 LTI 系统的哈,都是这个前提
一、LTI 连续系统的响应
在 LTI 系统中,最常见的数学模型为常系数线性微分方程。需要强调的是,我们所研究的对象是经过抽象的物理系统的数学模型,而不是物理系统本身。 其实就是建立 y(t) 与 f(t) 的关系式
y(t) : 响应函数
f(t) : 激励函数
1. LTI 微分方程的建立与求解
LTI 系统的建立,其实就是把实际的一些物理系统抽象称为 激励 - > 系统 -> 响应 模型
从符号来看其实就是 把 电流、电压、电阻 换成 f(t) y(t) 的关系式的过程 如下面例子。

2. LTI 连续系统的零输入响应与零状态响应
1. 零输入响应
- 系统的零输入响应 是指当系统的外加输入为零时,由系统的初始状态使系统产生的响应称为系统的零输入响应。
- 用符号 yx (t) 表示 可以不记住
2. 零状态响应
- 系统的零状态响应 是指当系统的初始状态为零时,由系统的外加激励使系统产生的响应称为系统的零状态响应。
- 用符号 yf (t) 表示 可以不记住
3. 全响应
- 零输入响应 + 零状态响应
- y(t) = yx (t) + yf (t)
二、冲激响应和阶跃响应
1. 冲激响应
当系统的激励为δ(t) 时,系统的零状态响应称为此系统的单位冲激响应,简称冲激响应。冲激响应一般用h(t)表示。

2. 阶跃响应
当系统的激励为u(t)时,系统的零状态响应称为此系统的单位阶跃响应,简称阶跃响应。一般用 g(t)表示。
当对激励进行数乘、延迟、微分以及积分运算时,其响应也应进行相同的运算。
阶跃响应与冲激响应具有如下关系

三、卷积积分及其性质
1. 任意信号的分解
其实就是利用了微分的数学定义
用 δ(t) 的积分表示信号

2. 任意信号作用下的零状态响应
求任意信号作用下 LTI 连续时间系统的零状态响应,可以先对任意信号进行分解,然后利用 LTI 连续时间系统的线性时不变特性求解。

这个是一种比较简单的求解时域方法。
3. 卷积的定义
我这里没说图解法、我用的很少
- f1 与 f2 的卷积积分为:
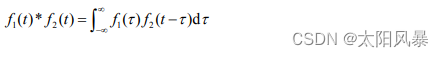
结合 信号分解的 思想,系统在任意激励信号 f (t)作用下的零状态响应 y (t)f 就可以用卷积积分的方法来求取,即
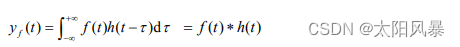
当已知系统的冲激响应h(t) 和激励信号 f (t)时,通过计算二者卷积积分的方法求取系统的零状态响应 yf(t)
4. 卷积性质
1. 代数性质
交换律:卷积积分是关于 f1(t) 和 f2(t) 对称的。
- f1(t) * f2(t) = f2(t) * f1(t)
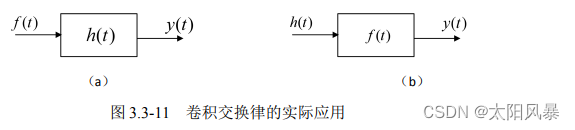
证明过程:
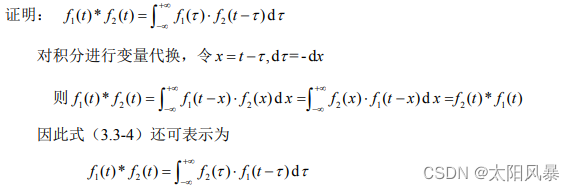
结合律:三个或三个以上函数的卷积结果与函数在卷积计算的次序无关。
- [ f1(t)* f2(t)]* f3(t) = f1(t) * [ f2(t) * f3(t)] = f2(t) * [ f3(t) * f2(t)]
分配律:
- [ f1(t)* f2(t)]* f3(t) = f1(t) * f3(t) + * f2(t) * f3(t)
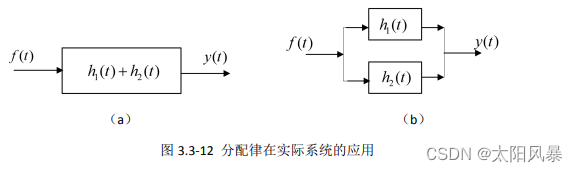
2. f(t)与奇异信号的卷积 (非常重要)
-
- 信号 f(t) 与冲激信号 δ(t) 的卷积等于 f(t) 本身
f(t) * δ(t) = f(t)

- 信号 f(t) 与冲激信号 δ(t) 的卷积等于 f(t) 本身
-
- 信号 f(t) 和冲激偶 δ’(t) 的卷积等于 f(t) 的导函数
f(t) * δ’(t) = f’(t)

- 信号 f(t) 和冲激偶 δ’(t) 的卷积等于 f(t) 的导函数
-
- 信号 f (t)与阶跃信号u(t)的卷积等于信号 f (t)的积分
f(t) * u(t) = f(-1)(t)
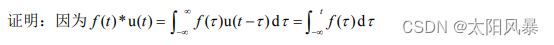
- 信号 f (t)与阶跃信号u(t)的卷积等于信号 f (t)的积分
3. 卷积的微分和积分
设 y(t) = f1(t) * f2(t)
-
- 微分
y(1)(t) = f(1)1(t) * f2(t) = = f1(t) * f(1)2(t)

- 微分
-
- 积分
y(-1)(t) = f(-1)1(t) * f2(t) = = f1(t) * f(-1)2(t)

- 积分
-
- 微积分
y(t) = f1(t) * f2(t) = f(-1)1(t) * f(1)2(t) = = f(1)1(t) * f(-1)2(t)

必须指出,使用卷积的微积分性质是有条件的,式(3.3-19)成立的条件要
求是:被求导的函数 f1(t) 或 f2(t) 在 t = -∞处为零值,或者被积分的函数 f1(t) 或 f2(t) 在(-∞,+∞)区间上的积分值(即函数波形的净面积)为零。而且,这里的两个条件是“或”的关系,只需要满足其中一个条件。
- 微积分
这里的可以推广哈
相当于把 指数值 可以做加减移到某一个信号的指数上
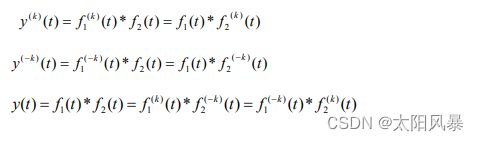
4. 卷积时移
设 y(t) = f1(t) * f2(t)
- f1(t - t0) * f2(t) = f1(t) * f2(t - t0) = y(t - t0) ; t0 是实常数

这里也可以推广
设 y(t) = f1(t) * f2(t)
- 则 f1(t - t0 - t1) * f2(t) = f1(t - t1) * f2(t - t0) = y(t - t0 - t1)
相当于把延时 可以做加减移到某一个信号上
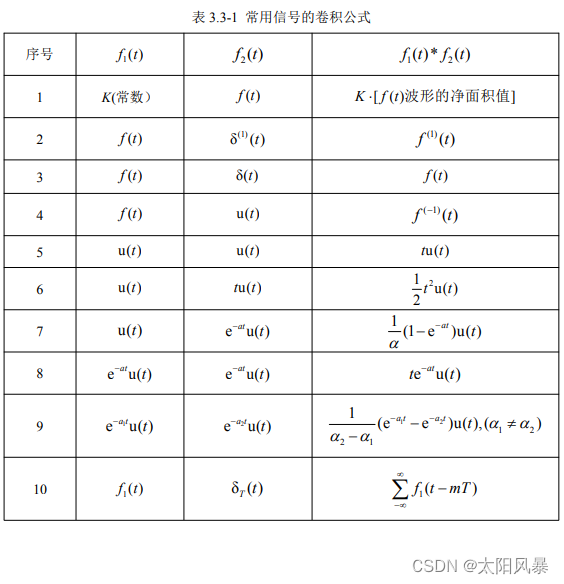
5. 常用信号的卷积公式
四、总结重点
重点是:
1、零输入、零状态响应的定义
2、卷积定义、性质、微积分、时移运算
3、卷积求零状态响应
一定要记住 卷积定义的公式,基本上性质和微积分、时移都是在定义的基础上推出来的
结论记不住,但可以推出来,很简单的一些积分
觉得不错的,可以点个赞哦~




![[附源码]java毕业设计校园共享单车系统](https://img-blog.csdnimg.cn/619f8aedbe5a404fa73cf6f37bb50e6b.png)