作者：张伟伟，来源：力学酒吧

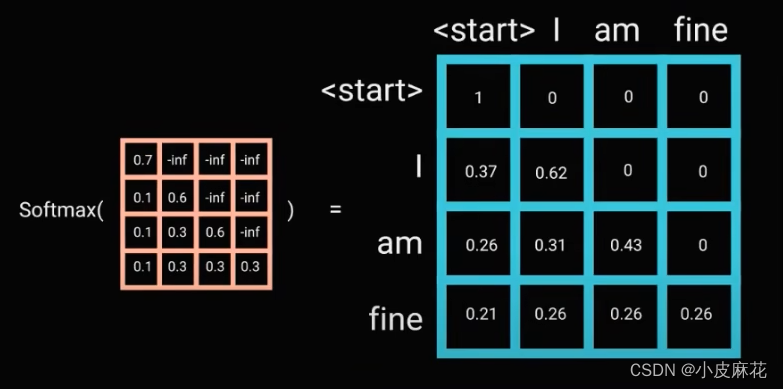
弹性力学基本方程包括平衡方程、几何方程和广义胡克定律，其中平衡方程和几何方程都属于微分方程。我们知道，在求解微分方程时，会出现积分常数，只有确定了积分常数，弹性力学问题的解才是唯一解。而确定积分常数的任务就落在弹性体的边界和边界条件上，围绕边界和边界条件，本文讨论三个问题，边界条件的分类，边界条件的本质，以及边界条件的数学表达，为弹性力学问题求解打下基础。

一、边界条件的分类与本质

如图1(a)所示，设有一被固定约束的弹性体，其边界上一部分受面力f 作用，另有一部分为自由状态。为了求出该弹性体的应力分布，需要先选取物体上任意一点P 点，如图1(b)所示，以该点为基准，建立微元体模型，通过分析该微元体的应力、应变、位移，建立弹性力学基本方程，并进行求解。

必须强调的是，任意选出的这一点一定不能是边界上的点，一旦所选取的点位于边界上，如P1、P2、P3，其受力和变形将会相应的受到边界上载荷和约束的限制。例如，弹性体内部的微元体，微面上的应力分量均来自于相邻微元体的作用，但边界上的微元体，将有一个微面成为边界的一部分，不再有相邻的微元体，此时的微元体的平衡将受边界上的外力限制；若边界微元体正好处于约束区域，其变形和位移又必将受到约束的限制，这些边界上的力和变形的限制统称为边界条件。

图1 弹性物体及其上一点处的微元体模型

如果边界上外力已知，称该边界条件为应力边界条件（如P3 点）；如果位移已知，则称之为位移边界条件（如P2 点）；特别地，对于自由边界（如P1 点，不受任何约束），可将其视为面力为0的应力边界条件。当某边界既有面力，同时又有位移约束时，称之为混合边界条件（如图1(a)整体边界）。应力边界条件、位移边界条件、混合边界条件，就是弹性力学问题的三类边界条件。

应力边界条件本质上反应了弹性体在边界上的平衡条件。假想弹性体被分割为无数个微元体，内部微元体满足平衡方程，如果我们可以一个个的观察微元体之间力的传递情况，直到边界上的微元体，一方面它与邻近微元体相连，另一方面受边界面力约束，可以建立应力与边界外力之间的平衡关系。

位移边界条件的本质也可以认为是满足平衡条件，因为位移约束可以由约束反力来等效，约束反力需要与应力之间形成平衡关系。例如求出图1(a)中的约束反力后，位移边界就转换为应力边界条件，就具有了应力边界条件的性质。

我们知道，材料力学的主要研究对象为细长结构，如杆、柱、梁、轴等，弹性力学区别于材料力学的重要特征就在于弹性力学突破了材料力学细长结构的局限，它可以解决任意形状的变形体力学，这正是由于弹性力学以微元体为研究对象，而微元体可以组成任意形状的物体，特别地，弹性体的边界和边界条件正是用来限定微元体组成物体的形状，并给出边界上受力和约束情况。

以下以平面问题为例，分别讨论如何对应力边界条件和位移边界条件进行数学描述。

二、应力边界条件

假设图1(a)所示弹性体满足平面应力（或平面应变）条件，该问题为平面应力（或应变）问题。考察边界上的点，不妨取P3 点为任意点P（若选P1 点面力分量为0），以该点为基准建立微元体PBC，如图2所示。这里，微面PB和PC上的应力分量由邻近微元体相互作用产生，微面BC为边界的一部分，习惯上也称其为斜面，受力由面力给出。斜面BC的方向由外法线方向n 分别与x轴、y 轴正向夹角的余弦确定，称之为方向余弦，并定义

点击完整阅读原文

弹性力学之边界条件

相关阅读推荐：

弹性力学物理方程

弹性力学之边界条件

兵哥讲透弹性力学