太原理工大学计算机控制技术实验之数字滤波实验

实验原理

一般现场环境比较恶劣，干扰源比较多，消除和抑制干扰的方法主要有模拟滤波和数字滤波两种。由于数字滤波方法成本低、可靠性高、无阻抗匹配、灵活方便等特点，被广泛应用，下面是一个典型数字滤波的方框图。

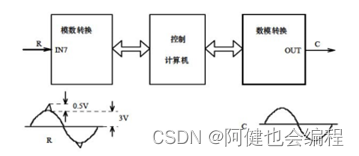
（1）一阶惯性滤波：
相当于传函1/(τs+1)的数字滤波器，由一阶差分法可得近似式

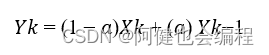
𝑋𝑘：当前采样时刻的输入
𝑌𝑘：当前采样时刻的输出
𝑌𝑘−1：前一采样时刻的输出
T：采样周期，1 − 𝑎 =T/τ
（2）四点加权滤波算法为：

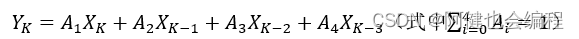
X_K：当前采样时刻的输入
X_(K-1)：前一采样时刻的输入
Y_K：当前采样时刻的输出

实验内容

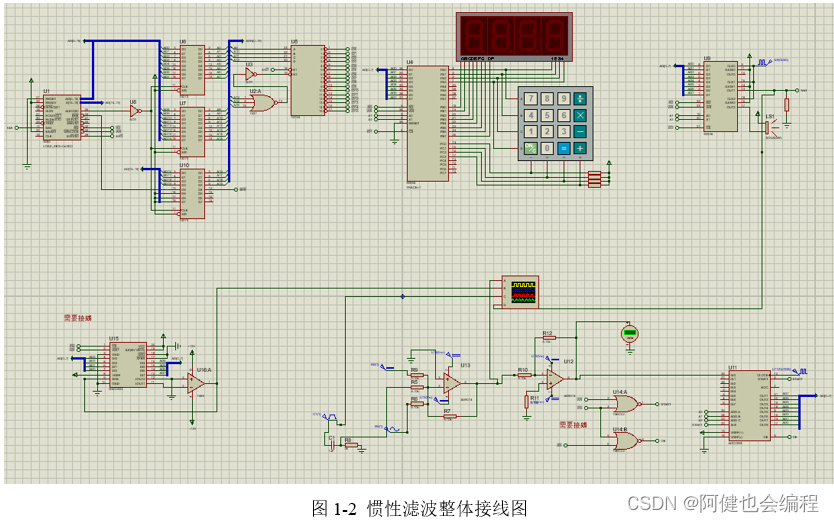
实验线路图设计

（1）惯性滤波

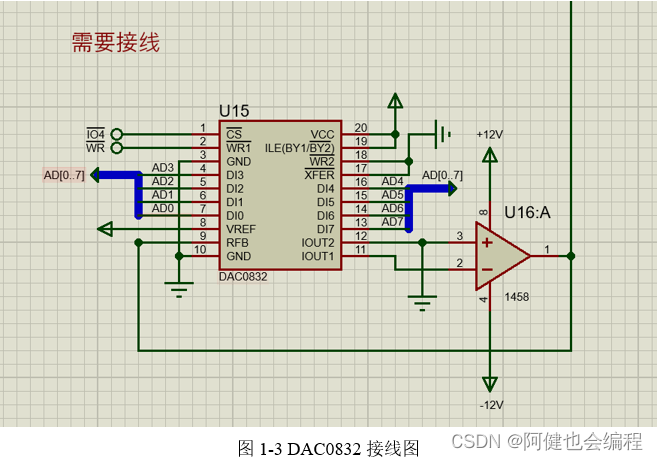
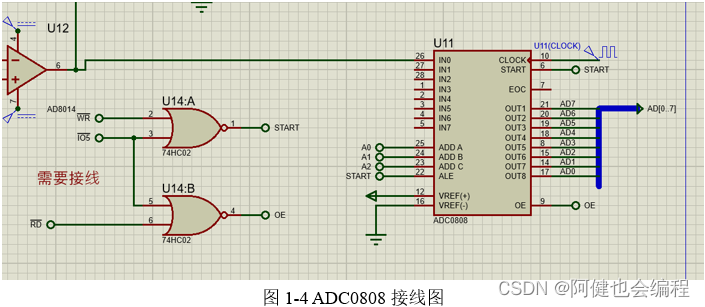
参考流程图

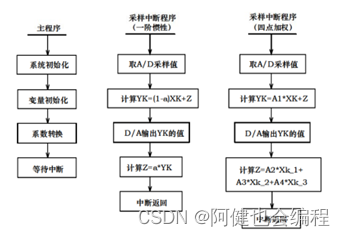
实验步骤及结果

采样周期设计

1）采样周期为5ms
8253A采用计数器2，时钟信号周期为10us，所以写入计数值0x01F4,则5ms产生一次中断信号，给8089的NMI，进入中断程序，使Sample_Mark=1,由于判断Sample_Mark=1,则进入AD转换，所以采样时间为5ms。

1）采样周期为40ms
8253A采用计数器2，时钟信号周期为10us，所以写入计数值0x01F4,则5ms产生一次中断信号，给8089的NMI，进入中断程序，使Sample_Mark++,由于判断Sample_Mark=8,则进入AD转换，所以采样时间为40ms。

运行结果

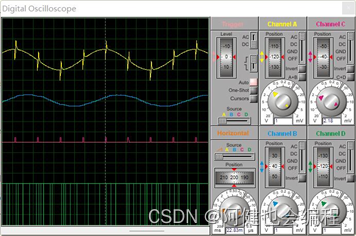
1）惯性滤波，采样周期为5ms
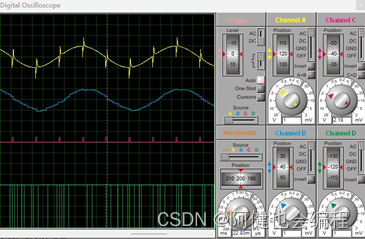
可以看出输出曲线相较于输入曲线平滑了一些，滤波作用较为明显。
黄线：给定信号源；
蓝线：经过滤波后的输出电压；
红线：给定的脉冲信号；
绿线：8253A输出的OUT1信号，定时产生中断信号。

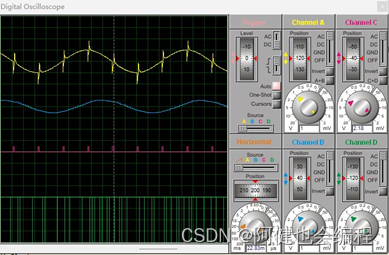
2）惯性滤波，采样周期为40ms
发现滤波曲线变得平滑，但是相较于5ms有所延迟。

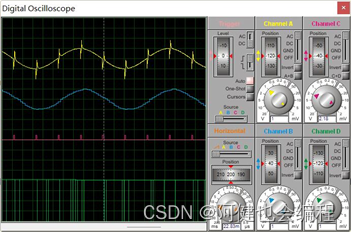
3）四点加权滤波，采样周期为5ms
滤波效果优秀，延迟较小。

4）四点加权滤波，采样周期为40ms
滤波效果较好，延迟较小，但波形有轻微波动。

思考题

1.思考实验中ADC0809的A、B、C端为什么要接+5V？
ADC0809 的 A、B、C 为通道选择信号，当 A、B、C 端接+5V 时，A、B、C端都是高电平，此时选通通道为 IN7.

2.试结合实验原理图和模电知识，说明尖峰噪声信号产生的原理

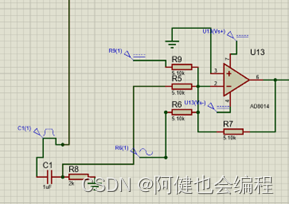
根据实验原理图可得，运算放大器U13与三个电压源U1、U2、U3构成了加法电路，则此时运算放大器的输出为：
Uout=-(U1+U2+U3)

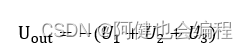
其中U1是2.5V的恒压源，U2是振幅为1V，频率为5Hz的正弦波，U3是幅值为1V，脉冲宽度为5%，频率为20Hz的脉冲信号，所以运算放大器的输出在恒压2.5V上叠加正弦波，并且有一个幅值为1V的脉冲信号，产生尖峰噪声。
3.实验中采样周期对滤波效果和输出信号有什么影响？
采样周期太大，采样频率就会变小，如果采样频率小于信号的最大频率的两倍，就会出现频率混送。采样周期越长，滤波效果就越明显，输出信号就越平滑，但是输出曲线出现明显的延迟。

4.实验中一阶惯性滤波的系数a和1-a与惯性时间常数有什么关系，试推导

一阶惯性环节的传递函数为：

(Y(s))/(X(s))=1/(τs+1)
可以得到：
τsY(s)+Y(s)=X(s)
采用后向差分可得：
τ (y(kT)-y((k-1)T))/T+y(kT)=x(kT)
化简可得（kT表示为k）：
y(k)=T/(τ+T) x(k)+τ/(τ+T) y(k-1)
由公式可得：
1-a=T/(τ+T)
a=τ/(τ+T)
由于T远远小于τ，所以一般简化为
1-a=T/τ