做题笔记。

下载 查壳。

64ida打开。

先运行一下程序：

那么，我们可以直接查找字符串看看，锁定位置。

### 纠正一下：应该是 n 值 不是d值 n = p*q 。。。### 

### v6的值 应该就是 我们func(input,49) 进行加密后的值。

(猜测的，毕竟逆向三分逆，七分猜测。。)

通过分析可以得到两个信息：

一        输入进行了加密。

二        进行了RSA加密。

那么，根据已知信息，这是通过 已知 C、e、n 去求m

所以。分两步：

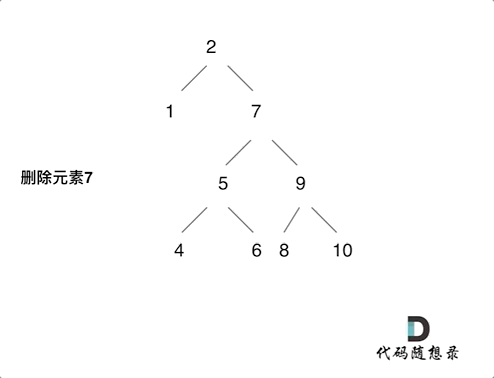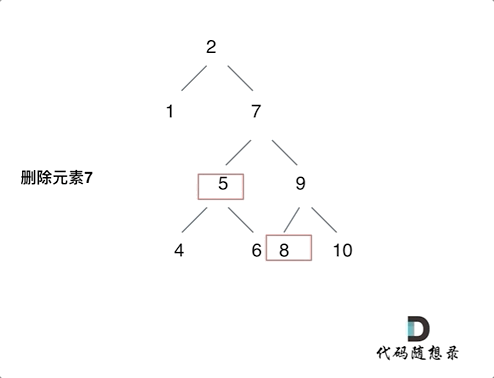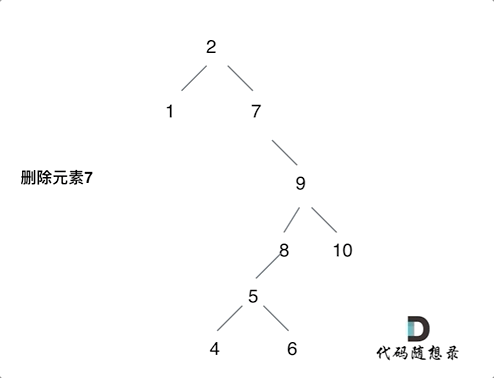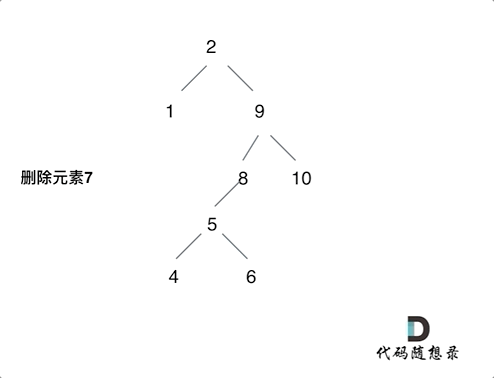
一        对n进行因式分解：

二        将密文从 hex 进行变成 dec （保持单位统一）：

总结已知信息：

对于，这种，使用C语言肯定不行的。用python去实现：

脚本：(前面的是我做的归类总结>>>此题在最后。)

关键库：

// import gmpy2---->实现RSA

// import binascii---->将RSA结果转成字符。

import gmpy2

"""
n=p*q       ->>>若n未知
import gmpy2
①invert(e,φ(N))  <<可以得到<<   L = (p-1)*(q-1)     d=gmpy2.invert(e,L)     求逆元快速算出来：invert(e,φ(N)) 求出d值。

②求明文m 或者 密文根据公式  密文 = 明文^e mod N     明文＝密文^D mod N
明文: m
m=gmpy2.powmod(c,d,n)
密文: c
c=gmpy2.powmod(m,d,n)

③dq、dp 是私钥的参数之一，分别表示d模p-1和d模q-1的余数的逆元。

注意！！！ dp和dq，他俩加上e、n和密文c全部已知的话是可以实现任意密文c解密

dp=d mod(p-1) dq=d mod(q-1) 即 dp=d % (p-1)  dq=d % (q-1) 

（当p\\q\\dp\\dq\\c/m已知的时候 密文一样 套用RSA原理。）
I = gmpy2.invert(q,p)
mp = pow(c,dp,p)               #求幂取模运算, mp = c^dp % p
mq = pow(c,dq,q)               #求幂取模运算, mq = c^dp % q
m = (((mp-mq)*I)%p)*q+mq       #求明文公式
"""

import binascii

"""
import binascii   # ->>>对于需要将进制转化成ASCII码显示时使用。
print(binascii.unhexlify(hex(m)[2:]).decode(encoding="utf-8")) 将数据变成字符串。(不行说明其本身没有对应的ASCII,也就是不需要转。直接上flag)

例子：
DEC 185534734614696481020381637136165435809958101675798337848243069
suctf{Pwn_@_hundred_years} ->>>正常输出。

5577446633554466577768879988 ->>>使用会报错。
"""

# 本题:
n = 103461035900816914121390101299049044413950405173712170434161686539878160984549
p = 282164587459512124844245113950593348271
q = 366669102002966856876605669837014229419

c = 78510953323073667749065685964447569045476327122134491251061064910992472210485

e = 65537

L = (p - 1) * (q - 1)
d = gmpy2.invert(e, L)
print(d)
m=gmpy2.powmod(c,d,n)
print(m)
print(binascii.unhexlify(hex(m)[2:]).decode(encoding="utf-8"))

suctf{Pwn_@_hundred_years}

题外话：

做到这里就可以提交了。。。 我还以为需要将其转成字符，在和key运算 还原输入。。

看来不用，大可能是我没有彻底理解…… 继续加油！