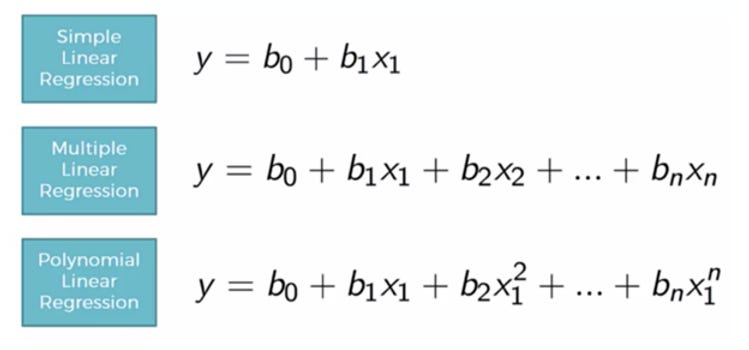
图 1.不同类型的回归
一、说明
非线性回归是指因变量和自变量之间存在非线性关系的模型。该模型比线性模型更准确、更灵活,可以获取两个或多个变量之间复杂关系的各种曲线。
二、关于
当数据之间的关系无法用直线预测并且呈曲线形式时,我们应该使用非线性模型。与线性回归不同,非线性模型中没有数据线性的假设。图 2 显示了线性和非线性数据。

图 2.线性数据(左侧)和非线性数据(右侧)
在图 2 中,横轴上与工作位置 (Position level) 和纵轴上的薪金 (Salary) 相关的数据表明这些数据具有非线性属性,线性回归显示了数据之间的关系。
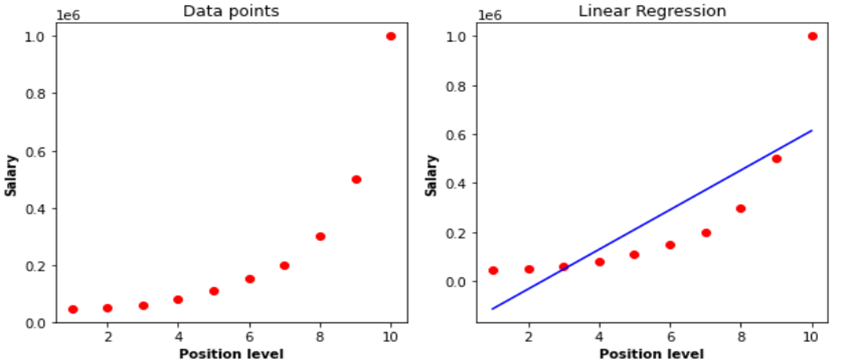
图 3.线性回归的数据(左侧)和拟合模型(右侧)
很明显,线性回归无法为数据拟合一条好的线,我们需要训练一个可以从数据中发现更复杂的关系的模型。因此,我们引入多项式回归来克服这个问题,这有助于识别自变量和因变量之间的曲线关系。
多项式回归是线性回归的一种形式,由于因变量和自变量之间的非线性关系,我们向线性回归添加了许多项以将其转换为多项式回归。这种方法是这样的,在训练模型之前,在预处理阶段,使用一种称为特征转换的方法,我们将线性回归转换为多项式。图 4 显示了从第一次(简单线性回归)到第四次的多项式。
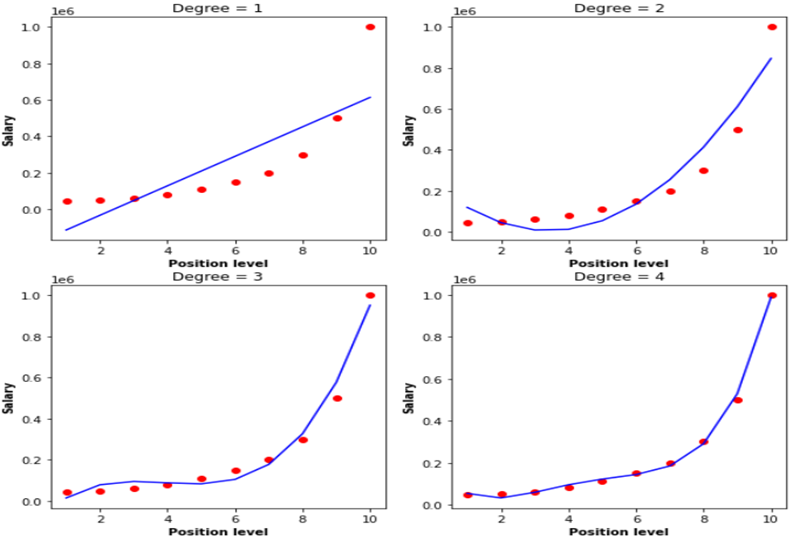
图 4.不同程度的多项式回归
在图 4 中,“Degree” 是指多项式次数,如您所见,一阶多项式是简单的线性回归,多项式次数越高,数据可以拟合的曲线就越复杂。
模型参数是在训练期间通过机器学习算法学习的值,例如线性回归中从原点开始的斜率和宽度;而超参数是由人类在训练之前确定的。多项式度是一个超参数,我们应该根据数据的复杂度来确定它。在学习过程中,高次多项式会导致过拟合,而低次多项式可能会导致欠拟合,因此我们必须为多项式选择最优的次数值(我将解释欠拟合和过拟合的精确和科学含义)。
三、理解多项式回归模型
3.1 监督机器学习
在监督学习中,算法使用标记数据集进行训练,并学习每个输入类别。我们使用测试数据(训练集的子集)评估该方法,并在完成训练阶段后预测结果。监督机器学习有两种类型:
- 分类
- 回归
3.2 分类与回归
| 回归 | 分类 |
|---|---|
| 预测连续变量 | 对输出变量进行分类 |
| 连续的 | 分类 |
| 天气预报、市场趋势 | 性别分类、疾病诊断 |
| 链接输入和连续输出 | 将输入分类 |
3.3 为什么我们需要回归?
回归分析有助于执行以下任务:
- 为了解解释成分的人预测因变量的值
- 评估解释变量对因变量的影响
3.4 什么是多项式回归?
在多项式回归中,我们使用 x 的 n 次多项式来描述独立变量 x 和因变量 y 之间的关系。多项式回归,表示为 E(y | x),表示拟合 x 值和 y 的条件均值之间的非线性关系。通常,这对应于最小二乘法。最小二乘法根据高斯-马尔可夫定理最小化系数方差。这代表一种线性回归,其中因变量和独立变量呈现曲线关系,并且多项式方程适合数据。
我们将在文章后面深入探讨这个概念。机器学习也是多元线性回归的一个子集,通过将额外的多项式元素纳入方程式,将其转换为多项式回归方程来实现。
四、 多项式回归的类型
二次方程是二阶多项式方程的统称。另一方面,这个次数可以达到 n 次。以下是多项式回归的分类:
- 线性 – 如果次数为 1
- 二次函数 – 如果次数为 2
- 三次——若次数为 3,则以次数为基础继续计算。

4.2 多项式回归假设
我们无法处理所有数据集并使用多项式回归机器学习来做出更好的判断。我们仍然可以做到这一点,但应该对数据集进行特定的约束,以便获得最佳的多项式回归结果。
- 因变量的行为可以通过因变量和一组 k 个独立因素之间的线性或曲线(加性联系)来描述。
- 独立变量之间缺乏任何相互关系。
- 我们采用具有独立分布误差的数据集,其服从正态分布,平均值为零,方差为常数。
4.3 用简单数学来理解多项式回归
这里我们处理数学,而不是深入研究,只需了解基本结构,我们都知道线性方程的方程是一条直线,如果我们有很多特征,那么我们选择多元回归,只增加特征部分,那么多项式怎么样,它不是增加而是将结构改变为二次方程,你可以从图中直观地理解:

4.4 线性回归与多项式回归
与其关注线性回归和多项式回归之间的区别,不如先从线性回归开始,这样我们就可以理解多项式回归的重要性。我们建立了模型,并意识到它的表现非常糟糕。我们检查实际值和我们预测的最佳拟合线之间的差异,看起来真实值在图表上有一条曲线,但我们的线远没有达到点的平均值。这就是多项式回归发挥作用的地方;它预测与数据模式(曲线)相匹配的最佳拟合线。
线性回归和多项式回归之间的一个重要区别是,多项式回归不需要数据集中的独立变量和因变量之间存在线性关系。当线性回归模型无法捕捉数据中的点,而线性回归无法充分表示最优值时,我们使用多项式回归。
在深入研究该主题之前,让我们首先通过编程和可视化来了解为什么在某些情况下我们更喜欢多项式回归而不是线性回归,比如数据集的非线性条件。
Python 代码
让我们使用回归分析来分析随机数据:
x = x[:, np.newaxis]
y = y[:, np.newaxis]
model = LinearRegression()
model.fit(x, y)
y_pred = model.predict(x)
plt.scatter(x, y, s=10)
plt.plot(x, y_pred, color='r')
plt.show()
直线无法捕捉数据中的模式。这是欠拟合的一个例子。
让我们从技术角度来看这个问题,使用均方根误差 (RMSE) 和判别系数 (R2) 等指标。RMSE 表示回归模型能够以绝对值预测响应变量的值,而 R2 表示模型能够以百分比形式预测响应变量的值。
import sklearn.metrics as metrics
mse = metrics.mean_squared_error(x,y)
rmse = np.sqrt(mse)
r2 = metrics.r2_score(x,y)
print('RMSE value:',rmse)
print('R2 value:',r2)
RMSE value: 93.47170875128153
R2 value: -786.23787532371034.5 多项式回归中的非线性数据
我们需要增强模型的复杂性来克服欠拟合。从这个意义上讲,我们需要以非线性的方式进行线性分析,在统计上,使用多项式,
![]()
因为与特征相关的权重仍然是线性的,所以这仍然是一个线性模型。x2(x 平方)只是一个函数。然而,我们试图拟合的曲线本质上是二次的。
让我们直观地看一下上述概念,以便更好地理解,一张图片比文字更有力,
from sklearn.preprocessing import PolynomialFeatures
polynomial_features1 = PolynomialFeatures(degree=2)
x_poly1 = polynomial_features1.fit_transform(x)
model1 = LinearRegression()
model1.fit(x_poly1, y)
y_poly_pred1 = model1.predict(x_poly1)
from sklearn.metrics import mean_squared_error, r2_score
rmse1 = np.sqrt(mean_squared_error(y,y_poly_pred1))
r21 = r2_score(y,y_poly_pred1)
print(rmse1)
print(r21)
49.66562739942289
0.7307277801966172图中清楚地显示二次曲线比直线更能吻合数据。
import operator
plt.scatter(x, y, s=10)
# sort the values of x before line plot
sort_axis = operator.itemgetter(0)
sorted_zip = sorted(zip(x,y_poly_pred), key=sort_axis)
x, y_poly_pred1 = zip(*sorted_zip)
plt.plot(x, y_poly_pred1, color='m')
plt.show()
polynomial_features2= PolynomialFeatures(degree=3)
x_poly2 = polynomial_features2.fit_transform(x)
model2 = LinearRegression()
model2.fit(x_poly2, y)
y_poly_pred2 = model2.predict(x_poly2)
rmse2 = np.sqrt(mean_squared_error(y,y_poly_pred2))
r22 = r2_score(y,y_poly_pred2)
print(rmse2)
print(r22)
48.00085922331635
0.7484769902353146
plt.scatter(x, y, s=10)
# sort the values of x before line plot
sort_axis = operator.itemgetter(0)
sorted_zip = sorted(zip(x,y_poly_pred2), key=sort_axis)
x, y_poly_pred2 = zip(*sorted_zip)
plt.plot(x, y_poly_pred2, color='m')
plt.show()

polynomial_features3= PolynomialFeatures(degree=4)
x_poly3 = polynomial_features3.fit_transform(x)
model3 = LinearRegression()
model3.fit(x_poly3, y)
y_poly_pred3 = model3.predict(x_poly3)
rmse3 = np.sqrt(mean_squared_error(y,y_poly_pred3))
r23 = r2_score(y,y_poly_pred3)
print(rmse3)
print(r23)
40.009589710152866
0.8252537381840246
plt.scatter(x, y, s=10)
# sort the values of x before line plot
sort_axis = operator.itemgetter(0)
sorted_zip = sorted(zip(x,y_poly_pred3), key=sort_axis)
x, y_poly_pred3 = zip(*sorted_zip)
plt.plot(x, y_poly_pred3, color='m')
plt.show()
与线性相比,我们可以观察到 RMSE 下降而 R2 分数增加。
五、过度拟合与欠拟合
我们不断增加度数,我们会看到最好的结果,但是如果我们得到的某个特定值的 r2 值为 100,就会出现过度拟合的问题。
在线性分析数据集时,我们遇到欠拟合问题
多项式回归可以纠正这个问题。
然而,当将度参数微调到最优值时,我们遇到了过拟合问题,导致 r2 值为 100%。结论是,我们必须避免过拟合和欠拟合问题。
注意:为了避免过度拟合,我们可以增加训练样本的数量,这样算法就不会学习系统的噪声,变得更加泛化。
5.1 偏差与方差的权衡
我们如何选择最佳模型?要解决这个问题,我们必须首先理解偏差和方差之间的权衡。
错误是由于模型在拟合数据时做出的简单假设而导致的,这种假设被称为偏差。偏差过大表明模型无法捕捉数据模式,从而导致拟合不足。
复杂模型试图匹配数据时所导致的错误称为方差。当模型方差较大时,它会忽略大多数数据点,从而导致数据过度拟合。
从上面的程序中,当度为 1 时(即在线性回归中),它表示欠拟合,即高偏差和低方差。而当我们得到 r2 值 100 时,即低偏差和高方差,即过拟合
随着模型复杂度的增加,偏差会减少,而方差会增加,反之亦然。理论上,机器学习模型应该具有最小的方差和偏差。然而,两者兼具几乎是不可能的。因此,必须做出权衡,以建立一个在训练数据和未知数据上都表现良好的强大模型。

5.2 维度 —— 如何找到适合自己的维度?
我们需要找到正确的多项式参数次数,以避免过度拟合和欠拟合问题:
- 前向选择:增加度参数,直到得到最优结果
- 向后选择:降低度参数,直到达到最优
六、损失和成本函数——多项式回归
成本函数是一种评估机器学习模型对给定数据集的性能的函数。成本函数是一个实数,用于计算预期值和期望值之间的差异。很多人不知道成本函数和损失函数之间的区别。换句话说,成本函数是数据中 n 个样本误差的平均值,而损失函数是单个数据点的误差。换句话说,损失函数指的是单个训练示例,而成本函数指的是完整的训练集。
均方误差也可以用作多项式回归的成本函数;但是,方程会有所不同。

我们现在知道成本函数的最优值是 0 或者接近于 0。为了得到最优的成本函数,我们可以使用梯度下降法,它可以改变权重,从而减少错误。
6.1 梯度下降 - 多项式回归
梯度下降是一种确定函数参数(系数)值的方法,目的是最小化成本函数(成本)。它可以降低成本函数(最小化 MSE 值)并实现最佳拟合线。
在函数开始时,斜率 (m) 和斜率截距 (b) 的值将设置为 0,并引入学习率 (α)。学习率 (α) 设置为一个极低的数字,可能在 0.01 和 0.0001 之间。学习率是优化算法中的一个调整参数,它设置每次迭代向成本函数最小值移动时的步长。然后根据成本函数方程的 m 确定偏导数,以及关于 b 的导数。

借助于下列方程,一旦确定了导数,a 和 b 就会得到更新。m 和 b 的导数已在上文推导完毕,为 α。
梯度表示损失函数最陡峭的上升,但最陡峭的下降是梯度的倒数,这就是为什么梯度从权重(m 和 b)中减去的原因。更新 m 和 b 值的过程一直持续到成本函数达到或接近理想值 0。m 和 b 的当前值将是最佳拟合线的最优值。
6.2 多项式回归的实际应用
我们将从导入库开始:
#with dataset
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
dataset = pd.read_csv('Position_Salaries.csv')
dataset
Segregating the dataset into dependent and independent features,
X = dataset.iloc[:,1:2].values
y = dataset.iloc[:,2].values
Then trying with linear regression,
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)视觉线性回归:
plt.scatter(X,y, color='red')
plt.plot(X, lin_reg.predict(X),color='blue')
plt.title("Truth or Bluff(Linear)")
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()
from sklearn.preprocessing import PolynomialFeatures
poly_reg = PolynomialFeatures(degree=2)
X_poly = poly_reg.fit_transform(X)
lin_reg2 = LinearRegression()
lin_reg2.fit(X_poly,y)七、多项式回归的应用
该方程通过各种实验技术获得结果。独立变量和因变量具有明确的联系。
- 用于查明沉积物中存在哪些同位素。
- 用于观察各种疾病在人群中的传播情况
- 合成创造的研究。
7.1 多项式回归的优势
因变量和自变量之间联系的最佳近似是多项式。它可以容纳各种各样的函数。多项式是一种可以容纳各种曲率的曲线。
7.2 多项式回归的缺点
数据中的一个或两个异常值可能会对非线性分析的结果产生重大影响。这些结果过于依赖异常值。此外,用于检测非线性回归中异常值的模型验证方法比线性回归中的方法要少。
八、结论
监督式机器学习包括分类和回归,其中回归对于预测连续值至关重要。多项式回归是一种回归形式,它捕捉复杂的关系,需要仔细选择度数以避免过度拟合或欠拟合。梯度下降优化了多项式模型,尽管存在固有的缺点,但仍在各个领域找到了实际应用。



![[OpenGL]使用OpenGL绘制带纹理三角形](https://i-blog.csdnimg.cn/direct/91a06c6a10f34ec6aa4d579d922d7328.png#pic_center)