题目描述

这是一道最小生成树Prim的模板题，本题与【模板】最小生成树Kruskal，仅仅只有nn和mm的大小不同
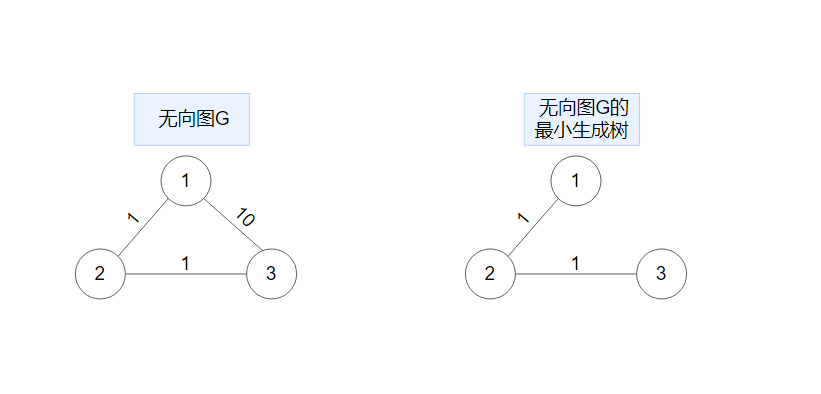
给出一个无向图，求出最小生成树，如果该图不连通，则输出orz
 

输入

第一行输入2个正整数n,mn,m，代表这个无向图有nn个点，mm条边。(1≤n≤1e3,1≤m≤2e6)(1≤n≤1e3,1≤m≤2e6)

后面输入m行，每行有33个正整数 x,y,zx,y,z，代表第i条边所连接的2个点和这条边的权值，可能存在重边。(1≤x,y≤n,1≤z≤10000)(1≤x,y≤n,1≤z≤10000)

本题输入输出过多
c++请用scanf输入printf输出,或者加入 ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);这段语句

输出

如果给的无向图是连通的，也就是能够求出一个最小生成树，请输出这个最小生成树的权值，否则请输出orz

样例输入1         复制

3 3
1 2 1
1 3 10
2 3 1

样例输出1         复制

2

提示

选择<1,2,1><2,3,1>这两条边此时可以生成一个最小生成树，此时权值也就是1+1=2

1. 我首先定义了常量N来表示节点的最大数量，以及定义了变量n、m、v、dis和ans，以及数组f。n表示节点的数量，m表示边的数量，v表示节点之间的边权值，dis表示每个节点到最小生成树的最小距离，ans表示最小生成树的权值，f表示节点是否已经加入最小生成树。

2. 在hs函数中，我首先通过输入获取了节点数量n和边的数量m。然后使用memset函数和循环，将二维数组v和一维数组dis初始化为正无穷，将数组f初始化为0。

3. 接下来，我通过输入获取了每条边的起点、终点和权值，并将权值存入二维数组v中。

4. 我将起始节点的最小距离初始化为0，并通过循环找到每个节点到最小生成树的最小距离，并将最小距离加入最小生成树的权值中。

5. 最后，我输出了最小生成树的权值。

下面是带注释的代码

#include <bits/stdc++.h>
using namespace std;
//定义各个常量与变量 
const int N=1e3+1;
int n,m,v[N][N],dis[N],ans=0;
bool f[N];


//真正的主函数 
void hs(){
	
	
	//  初始化 
	cin>>n>>m;
	memset(v,0x3f,sizeof(v));
	memset(dis,0x3f,sizeof(dis));
	memset(f,0,sizeof(f));
	for(int i=1;i<=m;i++){
		int p,q,x;
		cin>>p>>q>>x;
		if(x<v[p][q]){
			v[p][q]=x;
			v[q][p]=x;
		}
	}
	dis[1]=0;
	
	
	for(int i=1;i<=n;i++){
		int x=-1;
		for(int j=1;j<=n;j++)if(!f[j] && dis[j]<=10000 && ( x==-1||dis[j]<dis[x] ) )x=j;
		if(x==-1){//如果x等于-1，那么图不连通 
			cout<<"orz"<<"\n";//输出orz加换行 
			return ;//返回 
		}
		ans+=dis[x];
		f[x]=1;
		for(int j=1;j<=n;j++){
			if(!f[j])dis[j]=min(dis[j],v[x][j]);
		}
	}
	
	cout<<ans;//输出ans  
	
	return ;//返回 
}

int main() {//主函数 
	
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);//流加速 
    
    hs();//真正的主函数 
    
    return 0;//返回值 
}