前言
宽搜属于搜索类算法
搜索类算法:
- 深搜(DFS)
- 宽搜(BFS)
宽搜可以解决树、图、最短路径、迷宫、拓扑排序等问题
429. N 叉树的层序遍历
题目链接:429. N 叉树的层序遍历
题目解析
题目意思就是对这个N叉树进行一个层序遍历,记录每一层的结果
算法原理
这里每层遍历的时候,需要记录下一层的顺序,用一个队列来进行存储:
- 根节点不为空,根节点入队
- 队列不为空,
while循环,拿出对头元素,让对头元素的孩子入队 - 往后的操作都是,拿出对头元素,孩子入队,直到队列为空
这样要知道每一次多少个元素,只需在层序遍历之前,统计当前队列里的个数即可,当前队列里元素的个数,就是该层元素的个数
代码实现
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<vector<int>> levelOrder(Node* root)
{
queue<Node*> q;
vector<vector<int>> ret;
if(root == nullptr) return ret;
q.push(root);
while(!q.empty())
{
int cnt = q.size(); //该层元素的个数
vector<int> tmp; //记录本层节点的值
while(cnt--)
{
Node *cur = q.front();
q.pop();
for(const auto &e : cur->children) //下一层孩子入队
{
if(e != nullptr)
{
q.push(e);
}
}
tmp.push_back(cur->val);
}
ret.push_back(tmp);
}
return ret;
}
};
103. 二叉树的锯齿形层序遍历
题目链接:103. 二叉树的锯齿形层序遍历
题目解析
这次和上面一题差不多,只不过这里是二叉树,然后就是稍微修改了一下层序遍历的规则,这里的层序遍历是锯齿形(如下图)
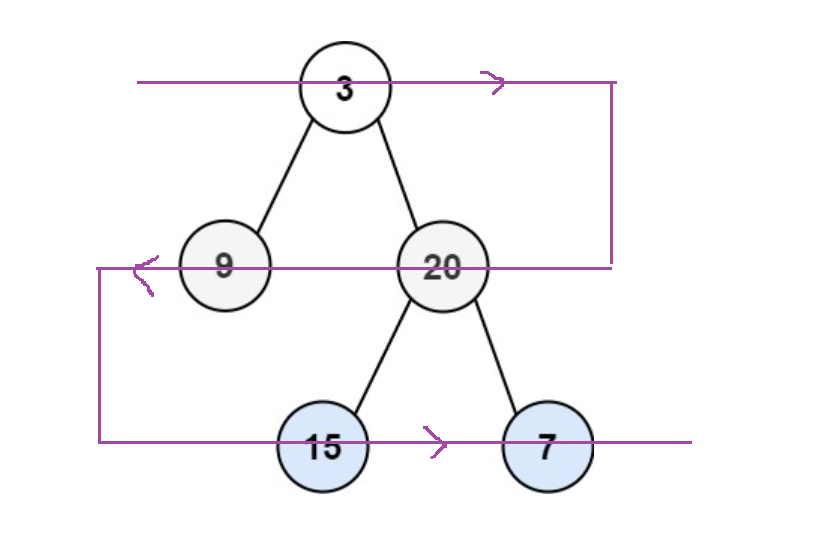
算法原理
还是采用层序遍历,然后加一个标记位,偶数行的数据逆序即可
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root)
{
queue<TreeNode*> q;
vector<vector<int>> ret;
bool flag = false;
if(root == nullptr) return ret;
q.push(root);
while(!q.empty())
{
vector<int> tmp;
int cnt = q.size();
while(cnt--)
{
TreeNode *cur = q.front();
q.pop();
if(cur->left) q.push(cur->left);
if(cur->right) q.push(cur->right);
tmp.push_back(cur->val);
}
if(flag)
{
reverse(tmp.begin(), tmp.end());
}
ret.push_back(tmp);
flag = !flag;
}
return ret;
}
};
662. 二叉树最大宽度
题目链接:662. 二叉树最大宽度
题目解析
这里统计所有层数当中的最大宽度。
这里的的宽度指的是从该层的最左和最右的非空节点的长度,如下图:
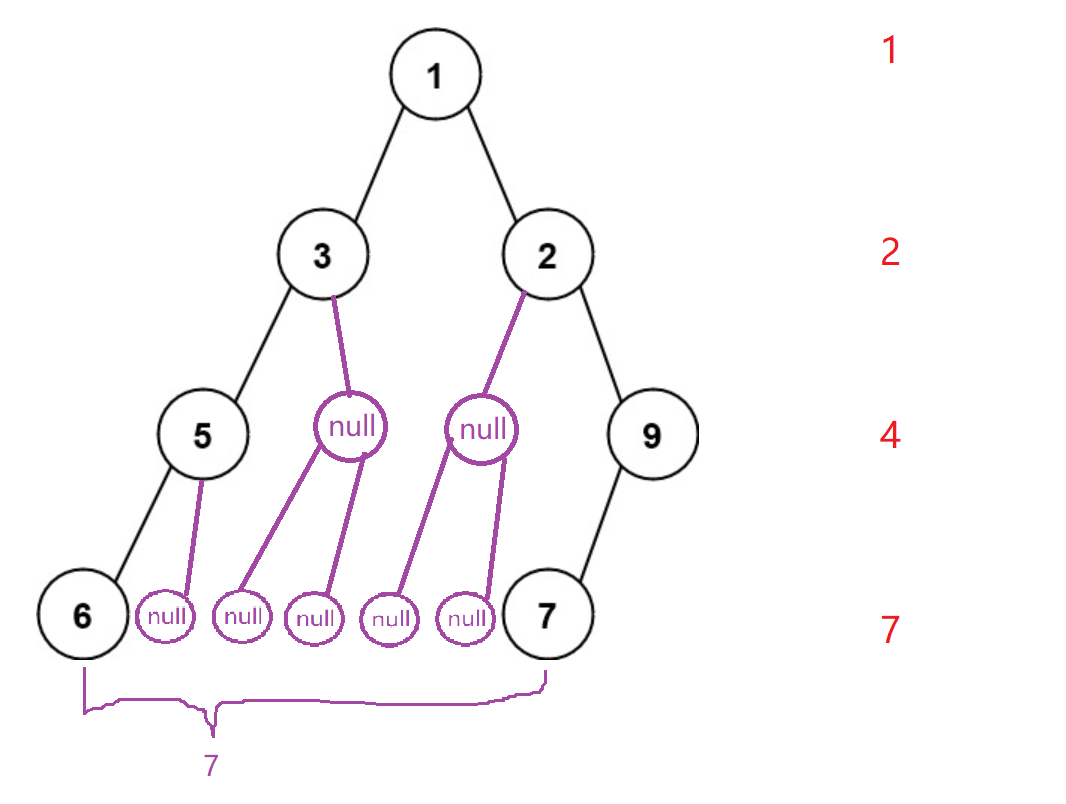
算法原理
解法1:
这里直接硬来,创建一个队列,因为要统计空节点的个数,所有直接将空节点也加入到队列当中,这样就能统计出当前层的宽度。
这样就会有一个问题:
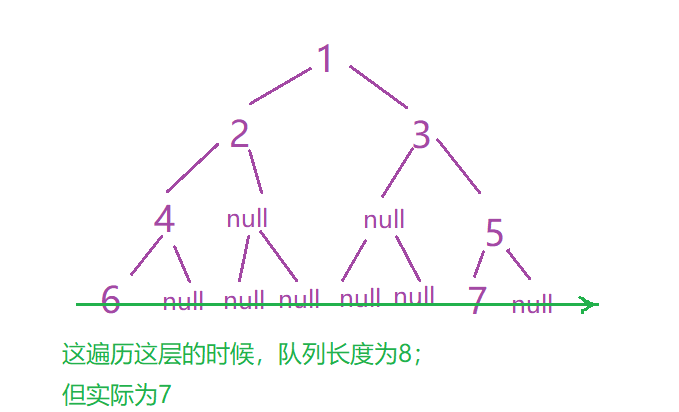
此时可以定义一个empty遍历,来统计空节点的个数,碰到不是空节点的时候,就算长度,然后再往后走,看看还有没有节点,有就更新。
这个会超时,因为数据是范围是[1, 3000]
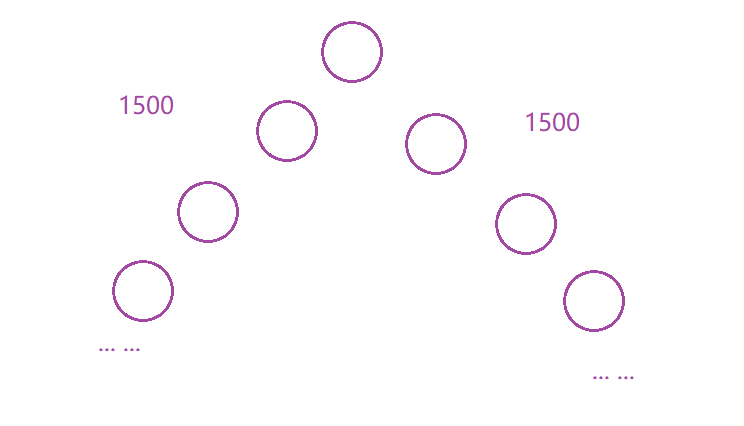
最后一层的节点个数约为21499,这个数据内存都存不下。
解法二:
树不仅可以链式存储,还可以利用数组存储,例如堆这个数据结构,它就是用数组来模拟的。
这样将树的节点编号,就不需要存储空节点了
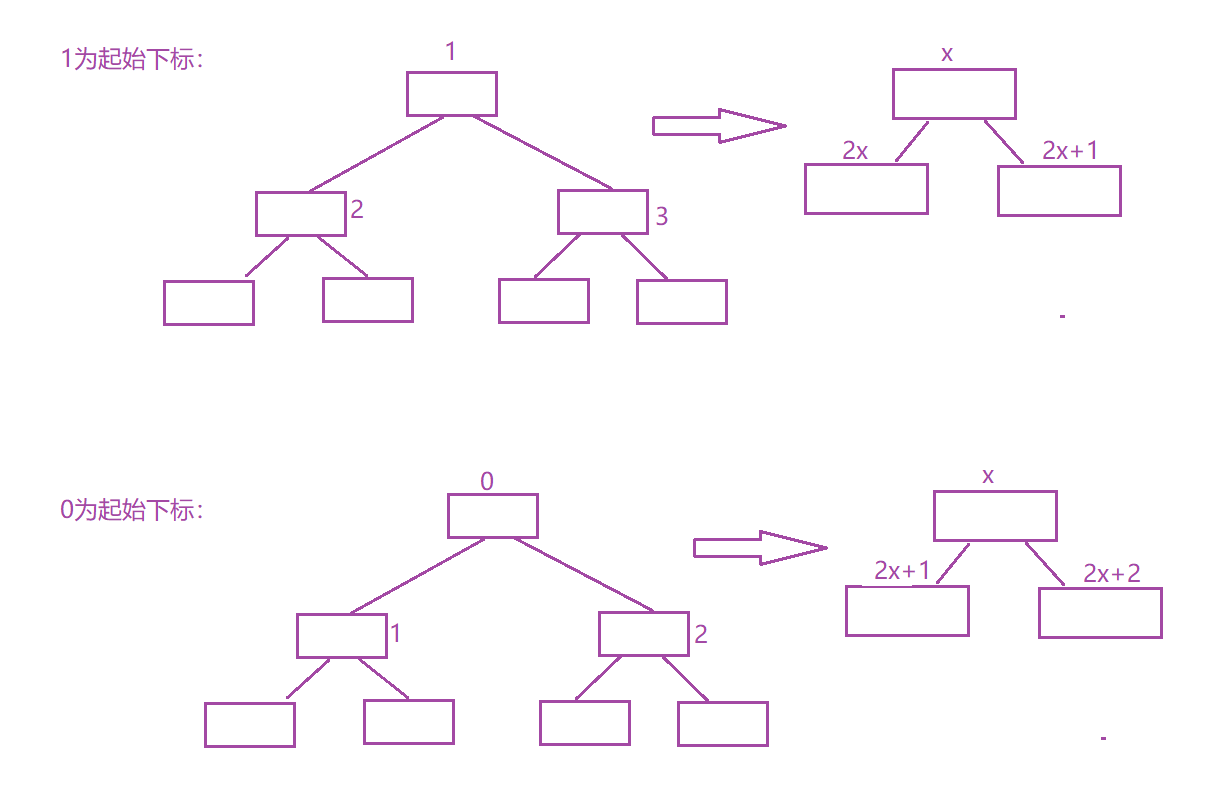
此时就可以创建一个队列,队列里面存一个pair<TreeNode*, int>,每次进队的时候,让该节点绑定它的编号,要计算宽度,只需要用队尾-队头+1
Tips1:
可以直接用数组模拟队列,这样非常容易找到队头及队尾。
此外,由于经常需要入队,数组的头删效率十分低下,为了避免这个问题,我们可以创建一个新数组,用改数组接收下一层的信息,然后直接覆盖之前的数组即可。
Tips2:
这个下标可能溢出,还是用解法一的超时用例举例,最下面一层的下标是21500 - 1,不管是long还是long long 还是double,都是存不下的。
不过不要紧,因为最后做减法,即使溢出结果也是正确的,因为数据的存储是可以看作一个环的
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int widthOfBinaryTree(TreeNode* root)
{
vector<pair<TreeNode*, unsigned int>> q;
q.push_back({root, 1}); //下标从1开始
unsigned int ret = 0;
while(q.size())
{
//计算该层宽度
auto& [x1, y1] = q[0];
auto& [x2, y2] = q.back();
ret = max(ret, y2 - y1 + 1);
//下一层进队
vector<pair<TreeNode*, unsigned int>> tmp;
for(auto &[x, y] : q)
{
if(x->left) tmp.push_back({x->left, y * 2});
if(x->right) tmp.push_back({x->right, y * 2 + 1});
}
//覆盖之前的
q = tmp;
}
return ret;
}
};
515. 在每个树行中找最大值
题目链接:515. 在每个树行中找最大值
题目比较简单,就不解析了
思路就是利用层序遍历,统计出每一层的最大值即可…
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> largestValues(TreeNode* root)
{
vector<int> ret;
if(root == nullptr) return ret;
queue<TreeNode*> q;
q.push(root);
while(!q.empty())
{
int tmp = INT_MIN;
int cnt = q.size();
while(cnt--)
{
TreeNode *cur = q.front();
tmp = max(tmp, cur->val);
q.pop();
if(cur->left)
{
q.push(cur->left);
}
if(cur->right)
{
q.push(cur->right);
}
}
ret.push_back(tmp);
}
return ret;
}
};