1.10 DFT示例1
Tips:离散傅里叶的不同角度的解释。
参考:https://mp.weixin.qq.com/s/TrRmqkc34Zqw9pgaITqlZg?poc_token=HF5h1WajXiXCmFpwIbv1HaHN52KsET1UE29CM561
摘取部分核心观点:
站在高观点下看问题,傅里叶变换本质上是求某函数在完备的函数空间中的坐标。
一个函数空间具有完备的正交函数系(类比三维空间具有三个基矢量),那么任意一个函数在该函数空间中都有一个“坐标”,而坐标的各个分量是该函数在各个基函数上的投影得到的。函数空间类比上面的二维平面和三维空间,任意一个函数则类比空间中的任意一个点,函数在各个基函数上的投影类比三维空间中一个点在各个坐标轴基矢量上的投影。
一个函数在这样的一种函数空间中的坐标表示,只是最基本的一种傅里叶展开。可以通过使用不同的函数系作为基函数从而得到不同的函数空间,从而引入广义的傅里叶展开。
例如,数学物理方法中我们所知道的对函数做贝塞尔展开、对函数做勒让德展开等,其实都是一种傅里叶展开,和读者所熟知的通常意义上的傅里叶变换本质上是相同的,都是在干一件事情:找寻一个函数在完备的函数空间中的“坐标”,即找到该函数在函数空间中各个基函数(基矢量)方向上的投影分量!唯一不同的是,贝塞尔展开中,函数“所处”的函数空间是由各阶贝塞尔函数作为基函数构成,而勒让德展开中,函数“所处”的函数空间是由各阶勒让德函数作为基函数构成。
1.10.1 矩形信号
矩形序列,无论是在时域还是频域中,都是DSP(数字信号处理)应用中遇到的最重要的信号之一。造成这种情况的原因之一是,任何在时域中具有有限持续时间的信号(例如T秒)(即所有实际信号)都可以看作是一个可能具有无限持续时间的信号与一个持续时间为T秒的矩形序列的乘积。这称为加窗(windowing) ,而矩形序列是最简单形式的窗口。
让我们计算长度为L的矩形序列的N点DFT:
$$s_l[n] = \begin{cases} 1, & n_s \leq n \leq n_s + L - 1 \\ 0, & \text{其他情况} \end{cases} \tag{1.62}$$如图1.59所示,其中N ≥ L。
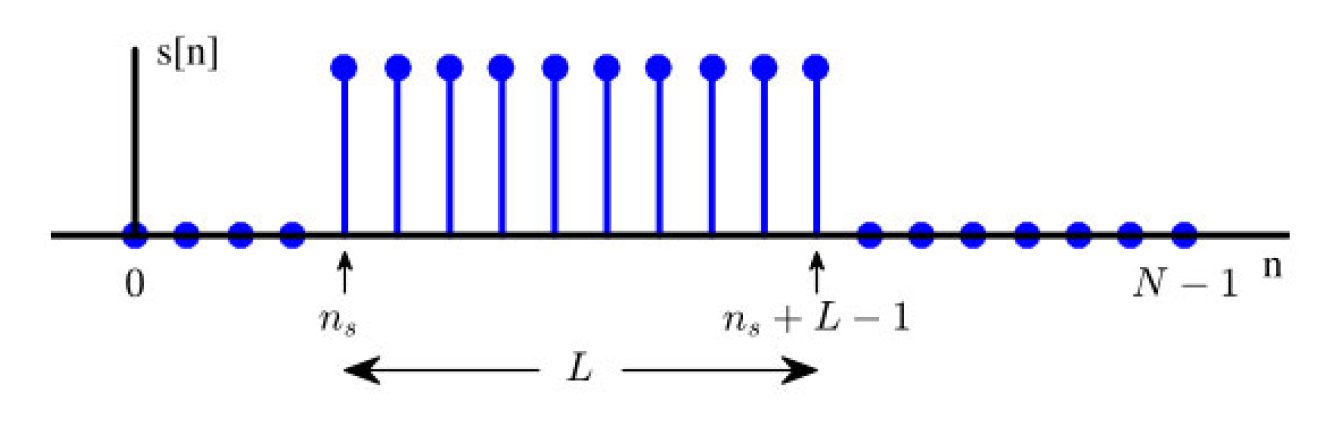
图1.59:一个长度为L的矩形序列,其中L < N。
由于这个序列在时域中是真实的,并且没有Q分量,因此DFT定义中频域的I分量可以表示为:
$$I \rightarrow S_I[k] = \sum_{n=0}^{N-1} s_I[n] \cos \left( 2\pi \frac{k}{N} n \right) = \sum_{n=n_s}^{n_s+L-1} \cos \left( 2\pi \frac{k}{N} n \right)$$$$= \sum_{n=n_s}^{n_s+L-1} \cos \left( 2\pi \frac{k}{N} n \right) \cdot \frac{\sin \left( \pi \frac{k}{N} \right)}{\sin \left( \pi \frac{k}{N} \right)} \tag{1.63}$$设 θ = 2 π k / N \theta = 2\pi k / N θ=2πk/N,并使用恒等式 2 cos A sin B = sin ( A + B ) − sin ( A − B ) 2 \cos A \sin B = \sin(A + B) - \sin(A - B) 2cosAsinB=sin(A+B)−sin(A−B),我们得到:
$$I \rightarrow S_I[k] = \sum_{n=n_s}^{n_s+L-1} \cos(n\theta) \frac{\sin(\theta/2)}{\sin(\theta/2)}$$$$= \frac{1}{2 \sin(\theta/2)} \sum_{n=n_s}^{n_s+L-1} \left[ \sin\left(\left(n + \frac{1}{2}\right)\theta\right) - \sin\left(\left(n - \frac{1}{2}\right)\theta\right) \right]$$$$= \frac{1}{2 \sin(\theta/2)} \left[ \sin\left(\left(n_s + L - \frac{1}{2}\right)\theta\right) - \sin\left(\left(n_s - \frac{1}{2}\right)\theta\right) \right]$$由于求和中的所有其他项相互抵消,使用上面相同的恒等式我们可以得到:
$$I \rightarrow S_I[k] = \frac{1}{\sin(\theta/2)} \cos\left(\left(n_s + \frac{L - 1}{2}\right)\theta\right) \cdot \sin\left(\frac{L\theta}{2}\right)$$$$= \frac{\sin\left(\frac{L\theta}{2}\right)}{\sin(\theta/2)} \cos\left(\frac{2\pi k}{N} \left(n_s + \frac{L - 1}{2}\right)\right) \tag{1.64}$$将表达式代入到 θ \theta θ中,我们得到:
$$I \rightarrow S_I[k] = \frac{\sin(\pi Lk/N)}{\sin(\pi k/N)} \cos\left[2\pi \frac{k}{N} \left(n_s + \frac{L - 1}{2}\right)\right] \tag{1.64}$$类似地,Q分量也可以通过DFT定义来求得:
$$Q \rightarrow S_Q[k] = \sum_{n=0}^{N-1} -s_I[n] \sin\left(2\pi \frac{k}{N} n\right) = \sum_{n=n_s}^{n_s+L-1} -\sin\left(2\pi \frac{k}{N} n\right) \tag{1.65}$$按照与I分量相同的步骤,并使用另一个恒等式 sin A sin B = 0.5 [ cos ( A − B ) − cos ( A + B ) ] \sin A \sin B = 0.5 \left[ \cos(A-B) - \cos(A+B) \right] sinAsinB=0.5[cos(A−B)−cos(A+B)],其DFT的Q分量由下式给出:
$$Q \rightarrow S_Q[k] = \frac{-\sin(\pi Lk/N)}{\sin(\pi k/N)} \sin\left[2\pi \frac{k}{N} \left(n_s + \frac{L - 1}{2}\right)\right] \tag{1.66}$$使用上述方程,对于全为1的矩形序列 L = N = 16 L = N = 16 L=N=16,图1.60绘制了所得DFT的I和Q部分。注意,当矩形序列覆盖从0到 N − 1 N-1 N−1 的所有可用时间域时,其DFT在频率0处只是一个脉冲。
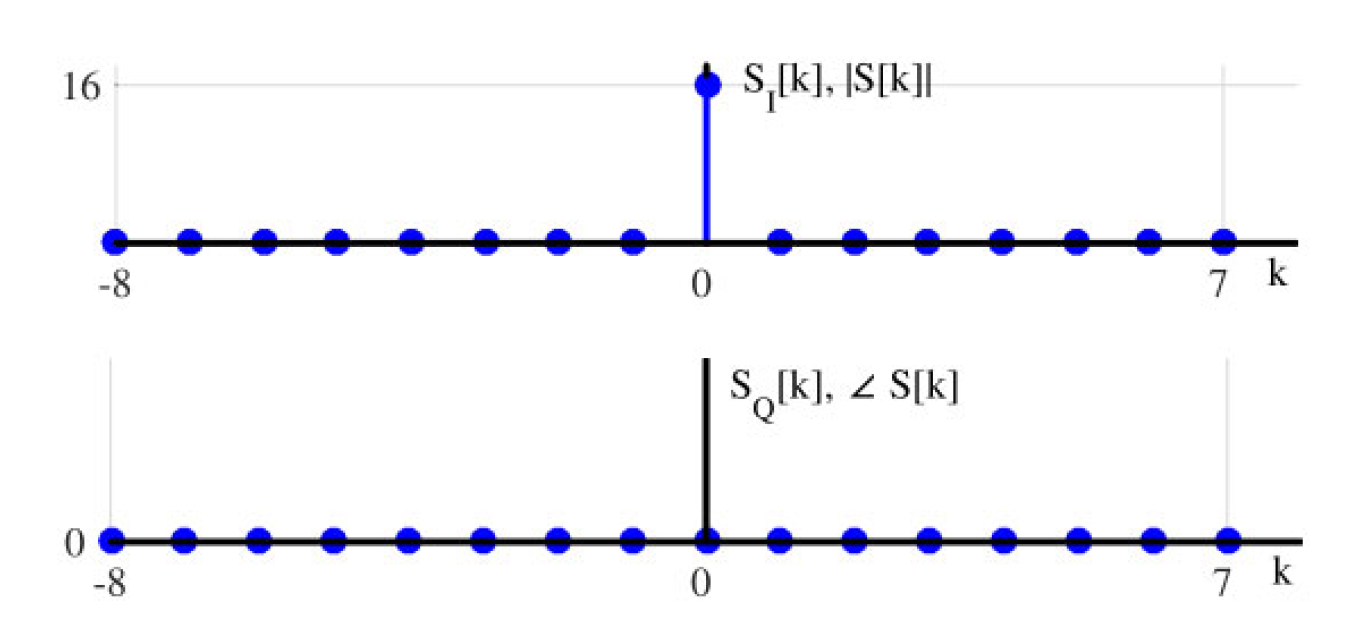
图1.60:全为1的DFT的幅度和相位(以及I和Q部分),对于 L = N = 16 L = N = 16 L=N=16。
尽管它很简单,但这里隐藏了很多信息,并且可以得出一些有趣的结论,因此我们将在下面继续讨论。
幅度和相位
将幅度和相位的定义应用到方程(1.64)和方程(1.66),并使用 cos 2 A + sin 2 A = 1 \cos^2 A + \sin^2 A = 1 cos2A+sin2A=1,我们得到矩形信号的DFT的幅度和相位:
$$|S[k]| = \frac{\sin(\pi Lk/N)}{\sin(\pi k/N)}$$$$\angle S[k] = -2\pi \frac{k}{N} \left(n_s + \frac{L - 1}{2}\right) \tag{1.67}$$当 L = N = 16 L = N = 16 L=N=16 时,图1.60还显示了矩形信号的DFT的幅度和相位图,在这种情况下,它们分别类似于I和Q图。第1.9节讨论了特定的 n s n_s ns 值如何影响相位图。
DFT,频域采样和泄漏
对于矩形信号的DFT,IQ方程如公式(1.64)和(1.66)所示,幅度相位关系如公式(1.67)所示。相应的图形在图1.60中绘制,单个脉冲在0点。
问题是:如此相对复杂的方程是如何生成如此简单的图形的?答案是,这是一种特殊情况,因为信号在时域中是全1的矩形序列。现在我们考虑如图1.61所示, L < N L < N L<N,其中 L = 7 L = 7 L=7, N = 16 N = 16 N=16,并且
$$n_s = -\frac{L - 1}{2} = -3$$这个选择的 n s n_s ns使信号在零点位置对称。同时,由于DFT输入周期性,这与 n s = N − L − 1 2 = 13 n_s = N - \frac{L-1}{2} = 13 ns=N−2L−1=13相同。就像之前一样,
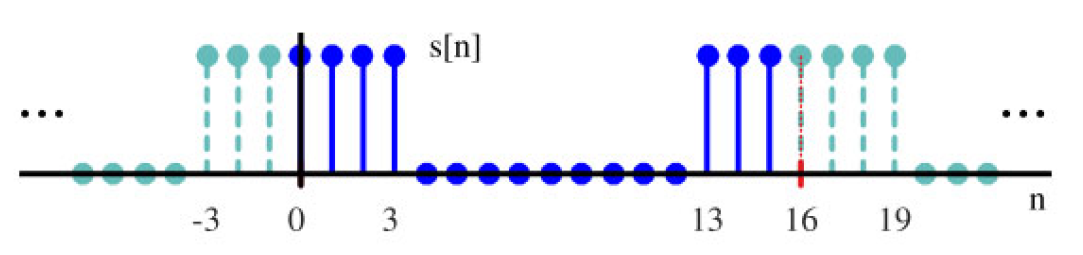
图1.61:从DFT计算角度来看,矩形序列的时域表示, n s = − ( L − 1 ) / 2 n_s = -(L-1)/2 ns=−(L−1)/2
可以通过像fft(·)这样的软件程序验证,这个仅有同相分量的偶数信号也有一个偶数DFT,并且仅有同相部分。
接下来,对于相同信号, L = 7 L = 7 L=7, N = 16 N = 16 N=16,设 n s = − ( L − 1 ) / 2 − 1 = − 4 n_s = -(L-1)/2 - 1 = -4 ns=−(L−1)/2−1=−4。该序列可以想象为从其对称位置向左移1,围绕零对称。图1.62中显示了来自方程(1.64)和(1.66)的I和Q图,以及来自方程(1.67)的幅度和相位图在图1.63中绘制。定义明确的sinc信号形式如下:
$$\text{sinc}(k) = \frac{\sin(\pi Lk/N)}{\sin(\pi k/N)} \tag{1.68}$$在离散频率 k / N k/N k/N的幅度图中可见。
现在我们可以认识到,图1.60中的图形也是sinc函数,但在0点处采样为峰值,并在其他所有点处为零。仔细观察sinc信号,理解其特性对DSP理解至关重要!
为了理解为什么该信号的能量出现在其他频率分析中,回顾DFT找到复正弦波在频率 F = F s ⋅ k / N F = F_s \cdot k/N F=Fs⋅k/N的贡献,对于 k = − N / 2 k = -N/2 k=−N/2到 N / 2 − 1 N/2-1 N/2−1的输入信号,这些都是基本频率 F s / N F_s/N Fs/N的整数倍。由于正交性,DFT能够找到每个 k t h k^{th} kth的贡献,独立于其他所有的贡献。如果输入信号仅包含从频率 k / N k/N k/N来的贡献,DFT的输出将与该频率相关的点成正比,而在其他所有点为零。
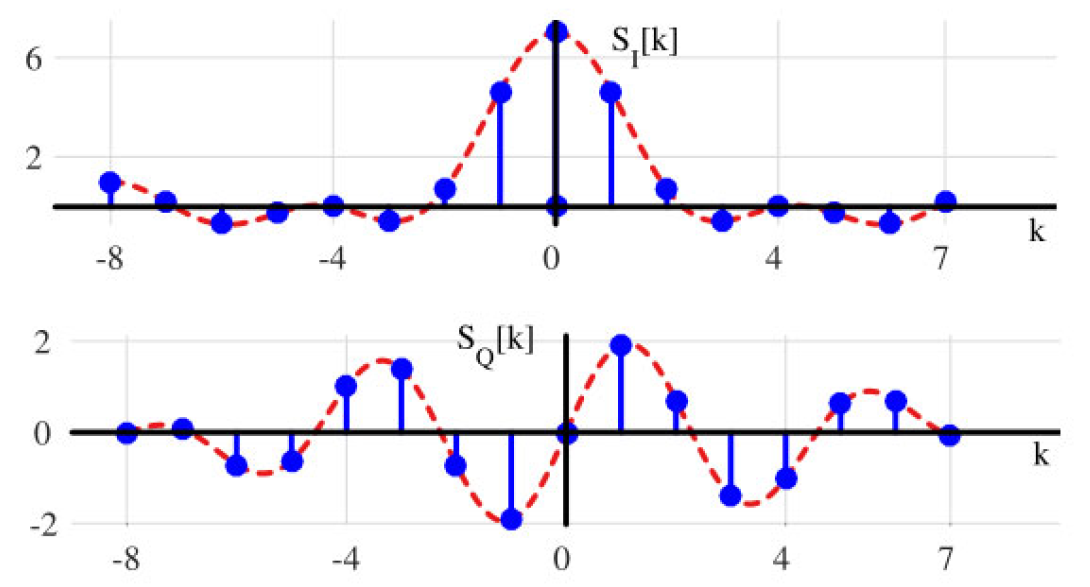
图1.62:矩形信号DFT的I和Q分量, L = 7 L = 7 L=7, N = 16 N = 16 N=16,且 n s = − ( L − 1 ) / 2 − 1 n_s = -(L-1)/2 - 1 ns=−(L−1)/2−1
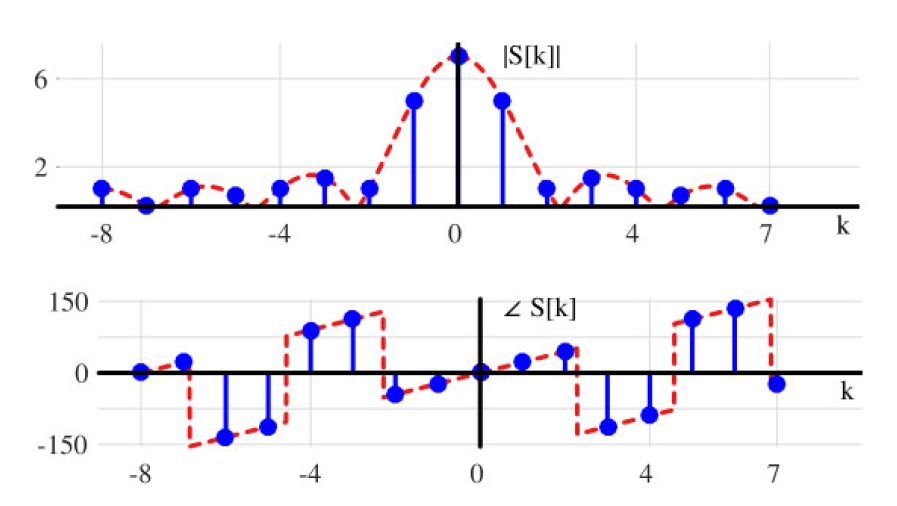
图1.63:矩形信号DFT的幅度和相位, L = 7 L = 7 L=7, N = 16 N = 16 N=16,且 n s = − ( L − 1 ) / 2 − 1 n_s = -(L-1)/2 - 1 ns=−(L−1)/2−1
对于全1矩形序列,当 L = N = 16 L = N = 16 L=N=16时,它实际上是一个单一复正弦波在离散频率0/N时,
$$I \quad \rightarrow \quad \cos \left( 2\pi \frac{k}{N} n \right) = \cos \left( 2\pi \frac{0}{N} n \right) = 1, \quad n = 0, \cdots, N - 1$$$$Q \quad \uparrow \quad \sin \left( 2\pi \frac{k}{N} n \right) = \sin \left( 2\pi \frac{0}{N} n \right) = 0, \quad n = 0, \cdots, N - 1$$因此,与其余 N − 1 N-1 N−1个复正弦波正交。因此,我们的DFT在 k = 0 k=0 k=0时为一个脉冲,而在其他 k k k处为零,见图1.60。
另一方面,其截断版本 L = 7 L=7 L=7, N = 16 N=16 N=16不是单一复正弦波。实际上,它由所有 N N N个正弦波组成,就像我们在图1.35中遇到的周期方波一样,因此能量分布在所有 N N N个频率格上。
在实际情况下,输入数据序列并不总是在给定的分析频率格上精确包含能量。如果输入信号在这些整数倍 F s / N F_s/N Fs/N之间的某个中间频率上有分量,比如 1.3 F s / N 1.3F_s/N 1.3Fs/N,则正交条件不成立,并且该输入信号将在DFT的所有输出格上显示出一定程度的能量。这被称为 DFT泄漏。
当我们对实际世界中的有限长度时间序列执行DFT时,DFT泄漏是不可避免的现象。让我们构建一个例子来详细观察这一点。
示例 1.6
假设一个频率为4 kHz的信号,采样率为 F S = 16 F_S = 16 FS=16 kHz。
$$s[n] = \sin \left( 2\pi \frac{4}{16} n \right)$$其中 N = 16 N = 16 N=16。实线蓝色曲线如图1.64a所示,是时域内的表示,分析频率 F 4 = F S ⋅ k N = 16000 ⋅ 4 16 = 4 F_4 = F_S \cdot \frac{k}{N} = 16000 \cdot \frac{4}{16} = 4 F4=FS⋅Nk=16000⋅164=4 kHz。注意,输入频率和分析频率 F 4 F_4 F4在采样间隔期间完成了四个完整的周期,因此其DFT,如图1.64b所示,在频率格4和-4处有两个脉冲,其他所有格上的输入为零。
实际曲线的形状是相同的 sinc函数,但它在频域内采样于恰好正确的位置,即,由于输入在时域内的整数周期数,采样于整数频率格。
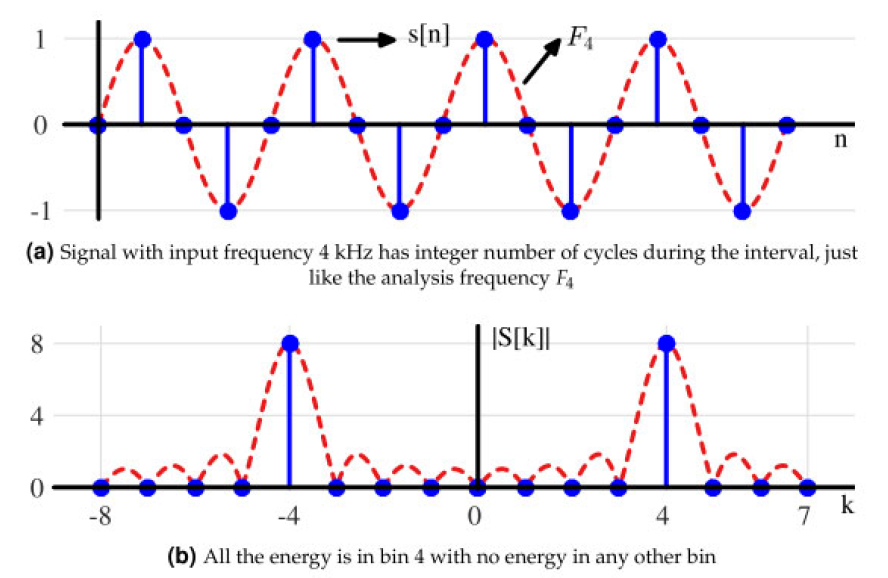
图 1.64:无 DFT 泄漏
现在让我们稍微改变输入信号,使其频率等于3.7 kHz,如图1.65a所示。
$$s[n] = \sin \left( 2\pi \frac{3.7}{16} n \right)$$注意,分析频率 F 4 F_4 F4在该区间内完成了四个完整的周期,而原始信号 s [ n ] s[n] s[n]中的3.7 kHz频率在16个采样间隔内没有整数个周期,破坏了正交性,导致输入能量泄漏到所有其他DFT输出格,如图1.65b所示。
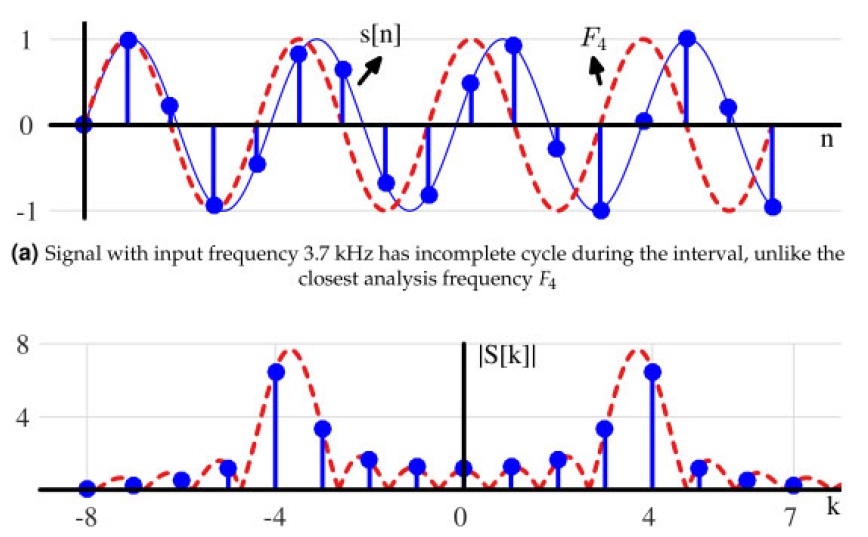
图1.65: DFT泄露
k = 3 k=3 k=3频率格不为零,因为输入序列和 k = 3 k=3 k=3分析频率的乘积之和不再为零(对于 k = 4 k=4 k=4也是如此)。这种泄漏导致任何频率不完全位于DFT格中心的输入信号泄漏到所有其他DFT输出格。sinc函数的形状没有变化,与4 kHz的输入相比,它只是以非理想点采样,即,由于输入在时域内的周期数不是整数,因此在频域内采样在分数频率格。
为什么会发生泄漏现象?想象一下,将滞后为0的相关过程视为频域中的采样过程,其中某个特定的分析频率“采样”了频谱。当输入信号的频率不是基本频率 F s / N F_s / N Fs/N 的整数倍时,频域采样不会发生在零交叉点处,从而引入所有N个参与者的干扰。
综上所述,频率不是 k / N k/N k/N 集的信号在观察窗口内不是周期性的,并且在未完成最后一个周期的情况下突然终止。这种不连续性违反了正交关系,产生了非零结果,并且导致频谱贡献扩展到频率 k / N k/N k/N 的整个集合中。
主瓣峰值
矩形信号的DFT在点 k = 0 k = 0 k=0 附近有一个主瓣。其幅度无法通过将 k = 0 k = 0 k=0 代入公式 (1.67) 中的正弦信号来求得,因为此时分子和分母都变为零,导致表达式为不定形式 0 / 0 0/0 0/0。虽然可以使用洛必达法则进行计算,但我们采取一种更简单的方法。**主瓣的峰值幅度为** ** L L L**,因为在 k = 0 k = 0 k=0 时,DFT定义规定:
$$S_I[0] = \sum_{n=0}^{N-1} s_I[n]$$$$S_Q[0] = \sum_{n=0}^{N-1} s_Q[n]$$这是因为 cos ( 2 π ( 0 / N ) n ) = 1 \cos(2\pi(0/N)n) = 1 cos(2π(0/N)n)=1 且 sin ( 2 π ( 0 / N ) n ) = 0 \sin(2\pi(0/N)n) = 0 sin(2π(0/N)n)=0。换句话说,DFT S [ 0 ] S[0] S[0] 是所有原始样本的总和。由于在此示例中 s Q [ n ] = 0 s_Q[n] = 0 sQ[n]=0,所以 L L L 个单位值样本的总和表现为 S I [ 0 ] = L S_I[0] = L SI[0]=L。因此,峰值被认为是 L = 16 L = 16 L=16 ,如图1.60所示,且 L = 7 L = 7 L=7 ,如图1.63所示。
DFT相位
直到现在,大部分讨论都围绕着幅度图展开。让我们通过矩形信号的DFT来理解相位的概念。现在,图1.66中绘制了图1.63的相位图,参数为 L = 7 L = 7 L=7, N = 16 N = 16 N=16,且 n s = − ( L − 1 ) / 2 − 1 n_s = - (L - 1) / 2 - 1 ns=−(L−1)/2−1。在消除由于更改 I 和 Q 符号而产生的 180° 相位跳变后,得到的相位是一条斜率为22.5°的直线。这个数值是从哪里来的?
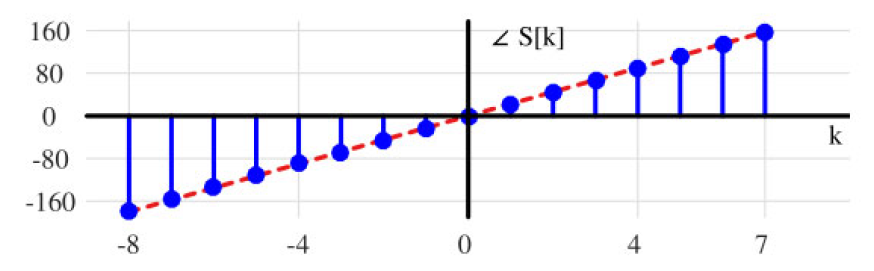
图 1.66:图 1.63 中的 DFT 相位,参数为 L = 7 L = 7 L=7, N = 16 N = 16 N=16 且 n s = − ( L − 1 ) / 2 − 1 n_s = - (L - 1) / 2 - 1 ns=−(L−1)/2−1,消除了 180° 的跳变。
我们在第1.9节的公式(1.58)中了解到,时间偏移 n 0 n_0 n0 个样本会导致每个 k k k 的相位旋转为 2 π ( k / N ) n 0 2\pi(k/N)n_0 2π(k/N)n0,其符号取决于时间偏移的符号。对于过去的时间旅行(即负偏移),相位旋转也是负的;而对于未来的时间旅行(即正偏移),相位旋转也是正的。
在我们的例子中,如果 n s = − ( L − 1 ) / 2 = 3 n_s = -(L - 1)/2 = 3 ns=−(L−1)/2=3,则将得到一个偶对称信号。此时, n 0 = 0 n_0 = 0 n0=0,相位图将如图1.67a所示,为0或π。
然而,对于 n s = − ( L − 1 ) / 2 + 1 n_s = -(L - 1)/2 + 1 ns=−(L−1)/2+1,这是一个右移(例如, L = 7 L = 7 L=7 时从-3移到-2)。因此,将 n 0 = − 1 n_0 = -1 n0=−1 代入公式 2 π ( k / N ) n 0 2\pi(k/N)n_0 2π(k/N)n0,会得出每个频率分段的相位旋转 Δ θ ( k ) \Delta\theta(k) Δθ(k)。
$$\Delta\theta(k) = 2\pi \frac{k}{N} n_0 = -2\pi \frac{k}{N}$$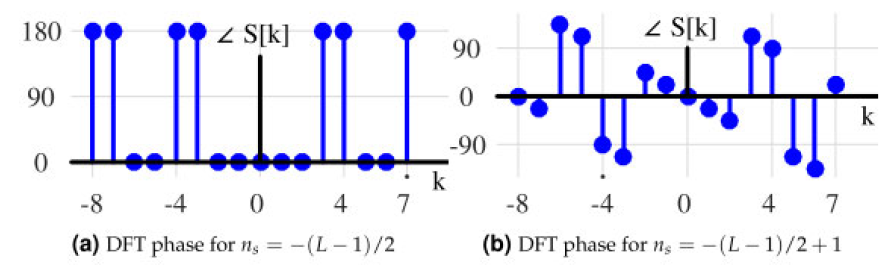
对于每个 k k k 从 − N / 2 -N/2 −N/2 到 N / 2 − 1 N/2 - 1 N/2−1。对于 N = 16 N = 16 N=16:
$$\Delta \theta(0) = 2\pi \times \frac{0}{N} \times \frac{180°}{\pi} = 0$$$$\Delta \theta(±1) = 2\pi \times \frac{±1}{N} \times \frac{180°}{\pi} = ±22.5°$$$$\Delta \theta(±2) = 2\pi \times \frac{±2}{N} \times \frac{180°}{\pi} = ±45°$$$$\Delta \theta(±3) = 2\pi \times \frac{±3}{N} \times \frac{180°}{\pi} = ±67.5°$$……
线性斜率为 -22.5°,由图 1.67b 验证,当调整了 180° 的相位跳跃后,跳跃是由于 sinc 函数幅度变化的符号引起的。