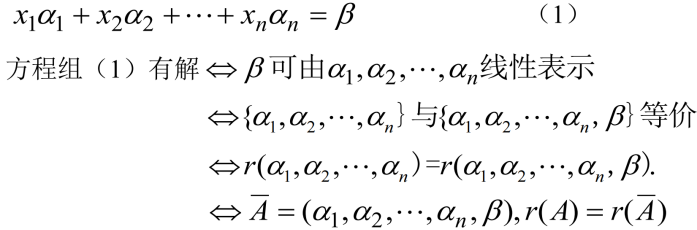目录
4.1 齐次线性方程组
4.1.1 齐次线性方程组的定义
4.1.2 方程组的三种形式
4.1.3 齐次线性方程组解的性质
4.1.4 行最简形矩阵
4.1.5 两个例题
4.2 基础解系的求法
4.2.1 求解步骤
4.2.2 例题
4.3 非齐次线性方程组
4.3.1 相关概念
4.3.2 非齐次线性方程组的有解判定
4.3.3 非齐次线性方程组的解的性质
4.3.4 非齐次线性方程组的通解
4.3.5 非齐次方程组的求解步骤
4.1 齐次线性方程组
4.1.1 齐次线性方程组的定义

如上形式的方程组被称为齐次线性方程组
该方程的系数矩阵为
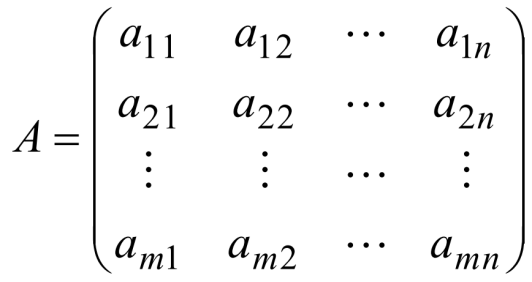
该方程的未知向量为
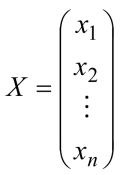
4.1.2 方程组的三种形式
代数形式、矩阵形式、向量方程形式
我们先来看代数形式
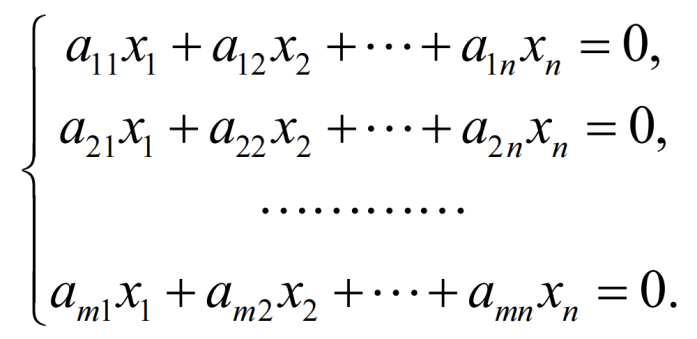
根据4.1.1中的系数矩阵和未知向量,我们得到矩阵形式为
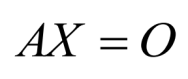
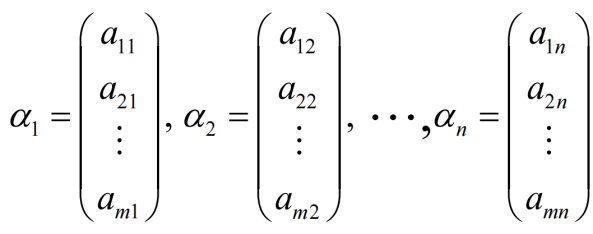
我们引进向量
然后我们就可以得到方程组的向量方程形式
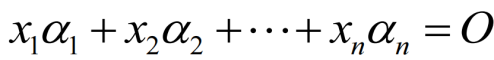
4.1.3 齐次线性方程组解的性质
性质1:齐次方程组的两个解的和仍是方程组的解
性质2:ξ是解向量,则kξ也是解向量
令V={ξ|Aξ= O},则V 构成一个向量空间,称为方程组的解空间

也就是说,我们将解空间的基称为基础解系,此时,通解就是基础解系的线性组合
4.1.4 行最简形矩阵
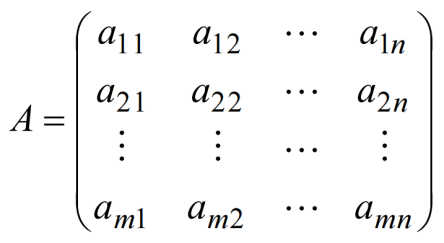
设 r(A) =r < n ,且不妨设A 中最左上角的 r 阶子式不为零。则经有限次行初等变换,矩阵 A 化为

显然

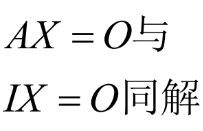
4.1.5 两个例题
例1:求解方程组
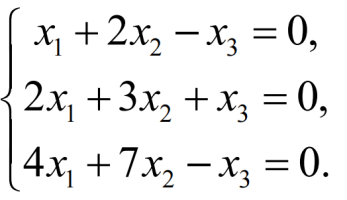
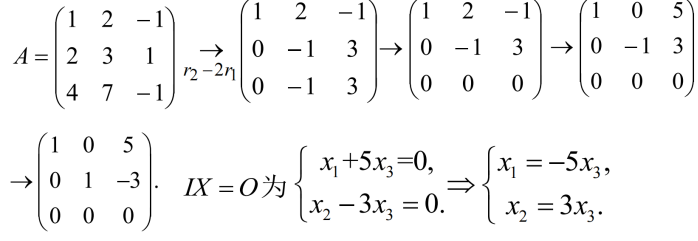
其中x3为自由未知量,x1、x2为真未知量
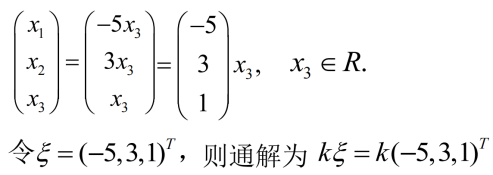
例2:求方程组的通解
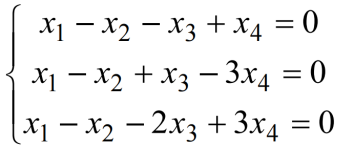

4.2 基础解系的求法
4.2.1 求解步骤
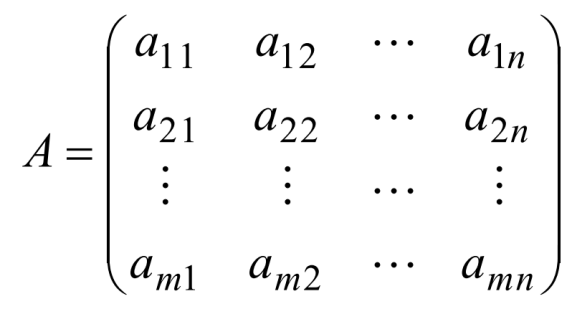
设 r(A) =r < n ,且不妨设A 中最左上角的 r 阶子式不为零。则经有限次行初等变换,矩阵 A 化为:
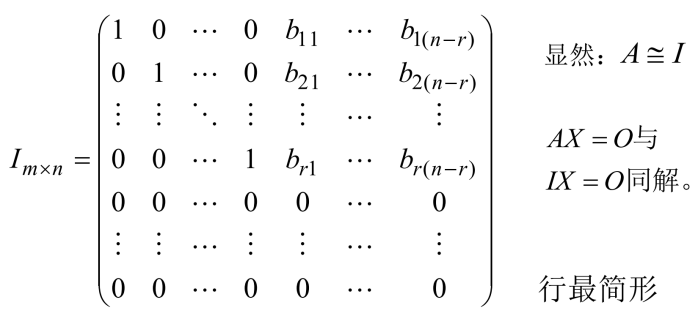
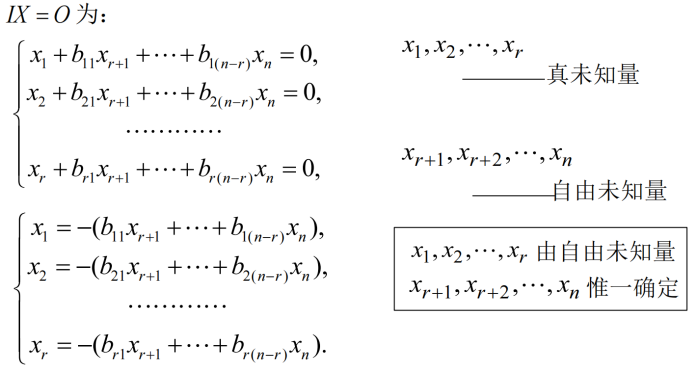



![]()
基础解系不惟一,但所含向量个数相等,都等于 n - r(A)
定理:若齐次线性方程组的系数矩阵A的秩r(A)= r< n,则它有基础解系,且基础解系所含解向量的个数为n-r
基础解系所含向量的个数为未知数个数减系数矩阵的秩
推论1:对齐次线性方程组,有
若 r(A)=n 则方程组有惟一零解;
若 r(A)=r<n ,则方程组有无数多解,其通解为
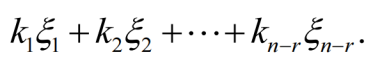
其中

是解空间的一组基础解系
步骤:
- 写出系数矩阵 A 并对其作初等行变换化为行最简形式(同时得到 r(A),这样也就可以确定基础解系所含解向量的个数);
- 由行最简形式确定真未知量和自由未知量并写出与原方程组同解的方程组;
- 对自由未知量赋值,求出基础解系(有几个自由未知量,就应赋几组值,将其视为向量组,它们是线性无关的)
4.2.2 例题
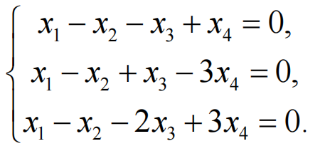
求方程组的通解

例题2

4.3 非齐次线性方程组
4.3.1 相关概念
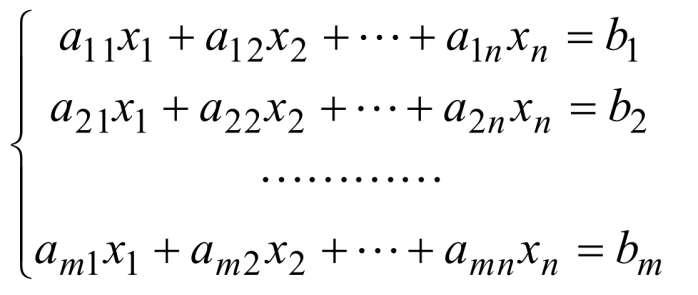
形如上图所示的方程组为非齐次线性方程组
其系数矩阵为
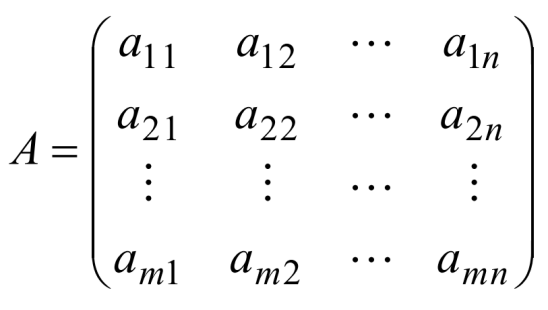
其未知向量为
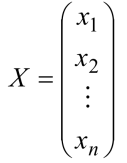
其常数向量为

与其对应的齐次线性方程组被称为该非齐次方程组的导出组
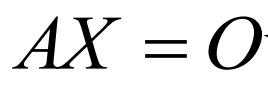
4.3.2 非齐次线性方程组的有解判定
其中
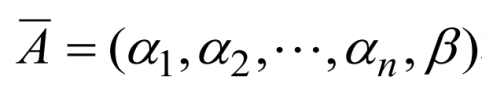
称为方程组(1)的增广矩阵
4.3.3 非齐次线性方程组的解的性质
性质1:非齐次方程组的两个解的差是它的导出组的解
性质2:非齐次方程组的一个解与其导出组的一个解的和还是该非齐次方程组的解
4.3.4 非齐次线性方程组的通解

推论

4.3.5 非齐次方程组的求解步骤
第一步

第二步

第三步