0、论文背景
本文在DE的基础上,提出了一种新的差分进化(DE)算法JADE,通过实现一种新的突变策略DE/current-to-pbest,采用可选的外部存档和参数的自适应更新,来提高优化性能。上述两种操作使种群多样化,并提高了收敛性能。
Zhang J, Sanderson A C. JADE: adaptive differential evolution with optional external archive[J]. IEEE Transactions on evolutionary computation, 2009, 13(5): 945-958.

1、JADE
JADE是在DE的基础上提出来的,有关DE,参见博客:DE。JADE采用了DE/current-to-pbest的突变策略,F和CR的值采用外部存档的方式动态自适应更新,JADE算法流程图如下所示。

1.1 DE/current-to-pbest
DE/current-to-pbest是在DE/current-to-best/1的基础上改进得到的,DE/current-to-best/1:
但是它有个问题,会出现收敛过早的情况。为了解决这个问题,为了增加突变后种群的多样性,提出了DE/current-to-pbest:
其中被随机选择为当前种群中前100p%的个体之一,p∈(0,1],p决定了突变策略的贪婪性,p越大,突变后种群的多样性越高。而
是从P∪A中随机选择的,引入A也是想提高突变后种群的多样性。
A为存档的次等解的集合,P为当前的总体。在迭代过程中,在选择过程中失败的种群将被添加到A中。如果存档大小超过了一定的阈值(NP),那么将从存档中随机删除一些解决方案,以保持A(存档)大小在NP。
1.2 F和CR的自适应
CR采用正太分布随机数,的初始值设置为0.5:
的更新为:
其中c是0和1之间的正数,c控制参数自适应的速率。meanA(·)是通常的算术平均值。是每次选择成功后的种群的CR值集合。
F采用柯西分布随机数,因为与正态分布相比,柯西分布更有利于使突变因子多样化,从而避免了贪婪突变策略中经常发生的过早收敛,的初始值设置为0.5:
meanL(·)是Lehmer的平均值:
Lehmer均值有助于传播更大的突变因子,而F越大,有助于增加种群多样性,防止过早收敛。
2、算法的复现和简单实验
有关SaNSDE,请参见博客:SaNSDE。
JADE复现代码:
function [globalBest, globalBestFitness, FitnessHistory] = JADE(popsize, maxIteration,dim, LB, UB, Fun)
Sol(popsize, dim) = 0; % 种群的初始化和计算适应度值
Fitness(popsize) = 0;
for i = 1 : popsize
Sol(i, :) = LB + (UB - LB) .* rand(1, dim);
Fitness(i) = Fun(Sol(i, :));
end
[fbest, bestIndex] = min(Fitness); % 获得全局最优值以及对应的种群向量
globalBest = Sol(bestIndex, :);
globalBestFitness = fbest;
muCR = 0.5; % 相关变量的初始化
muF = 0.5;
A = [];
p = 0.05;
c = 0.2;
for time = 1 : maxIteration
SF = [];
SCR = [];
for i = 1 : popsize
CR = normrnd(muCR, 0.1); % 正太随机数
%pd = makedist('tLocationScale', 'mu', muF, 'sigma', 0.1, 'nu', 1);
% F = random(pd, 1, 1);
F = Cauchy_rand(muF, 0.1); % 柯西随机数
[~, sortIndex] = sort(Fitness); % 随机选择前 popsize * p 对应的 xPBest
sortSol = Sol(sortIndex, :);
xPBest = sortSol(randi(p * popsize), :);
r1 = randi(popsize);
while r1 == i
r1 = randi(popsize);
end
SolA = [Sol; A];
r2 = randi(size(SolA, 1));
while r2 == r1 || r2 == i
r2 = randi(size(SolA, 1));
end
mutantPos = Sol(i, :) + F * (xPBest - Sol(i, :)) + F * (Sol(r1, :) - SolA(r2, :)); % 突变
jj = randi(dim); % 选择至少一维发生交叉
for d = 1:dim
if rand() < CR || d == jj
crossoverPos(d) = mutantPos(d);
else
crossoverPos(d) = Sol(i,d);
end
end
crossoverPos(crossoverPos>UB) = UB(crossoverPos>UB); % 检查是否越界
crossoverPos(crossoverPos<LB) = LB(crossoverPos<LB);
evalNewPos = Fun(crossoverPos); % 将突变和交叉后的变量重新评估
if evalNewPos < Fitness(i) % 小于原有值就更新
A = [A; Sol(i,:)];
if size(A, 1) > popsize
A(randi(size(A, 1)), :) = []; % 保持A的数目不超过popsize
end
SCR = [SCR; CR];
SF = [SF; F];
Sol(i,:) = crossoverPos;
Fitness(i) = evalNewPos;
end
end
muCR = (1 - c) * muCR + c * mean(SCR);
muF = (1 - c) * muF + c * (sum(SF .* SF) / sum(SF));
[fbest, bestIndex] = min(Fitness);
globalBest = Sol(bestIndex,:);
globalBestFitness = fbest;
FitnessHistory(time) = fbest; % 存储每次迭代的最优值
end
endclc;clear;clearvars;
addpath('CEC2008\');
global initial_flag
initial_flag = 0;
% 初始化变量维度,种群数,最大迭代次数,搜索区间,F,CR
dim = 30;
popsize = 100;
maxIteration = 1000;
LB = -100 * ones(1, dim);
UB = 100 * ones(1, dim);
F = 1;
CR = 0.9;
[globalBest, globalBestFitness, FitnessHistory] = DE(popsize, maxIteration,dim, LB, UB, F, CR, @(x)benchmark_func(x,1));
[globalBest1, globalBestFitness1, FitnessHistory1] = JADE(popsize, maxIteration,dim, LB, UB, @(x)benchmark_func(x,1));
[globalBest2, globalBestFitness2, FitnessHistory2] = SaNSDE(popsize, maxIteration,dim, LB, UB, @(x)benchmark_func(x,1));
plot(FitnessHistory);
hold on;
plot(FitnessHistory1);
hold on;
plot(FitnessHistory2);
legend('DE','JADE','SaNSDE','Location', 'northeast');
函数1测试结果:
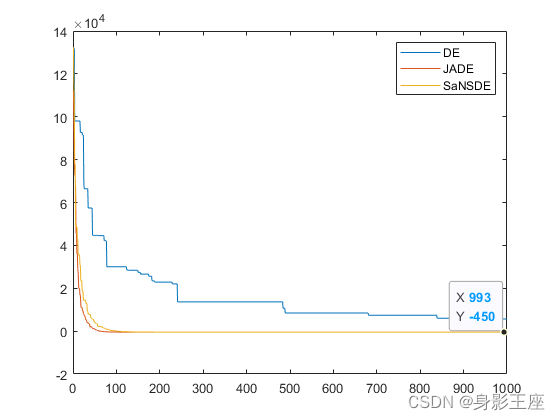
函数2测试结果:
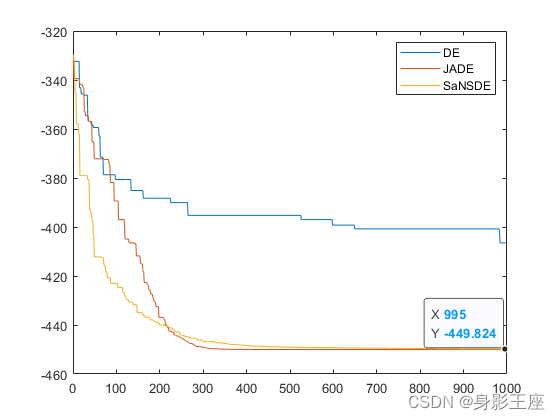
函数3测试结果:
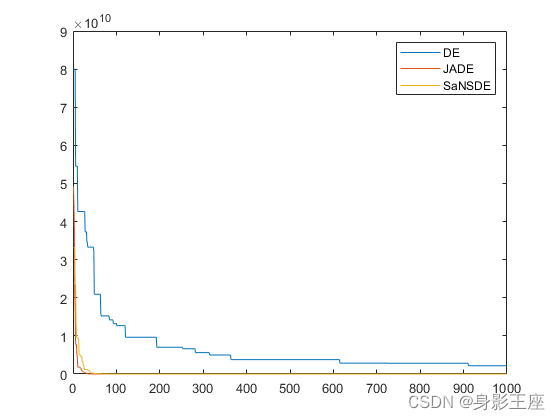
如有错误,还望批评改正!





![[附源码]java毕业设计网上博物馆设计](https://img-blog.csdnimg.cn/27513fbaf65d4d32a469d2466716557b.png)