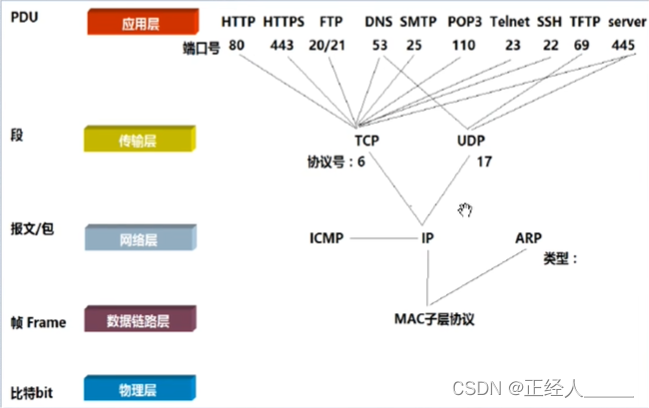
求两个字符串的最长公共子序列长度。
输入格式:
输入长度≤100的两个字符串。
输出格式:
输出两个字符串的最长公共子序列长度。
输入样例1:
ABCBDAB
BDCABA
输出样例1:
4
输入样例2:
ABACDEF
PGHIK
输出样例2:
0(1条消息) HBU训练营【动态规划DP】——最长公共子序列长度 (15分)_Fmm-PMO的博客-CSDN博客 //题目短,代码也短,但是代码中蕴含的算法思维却是需要好好理解,参考了上面博主的代码,这道题或许短时间内,我们能够记住,但是一段时间后就不一定会做了,所以最好是能够理解代码。
//本题核心就是循环加判断部分,运用了动态规划(DP),关于最长公共子序列我们借用该播主的内容,
//也就是两个字符串从左往右不可逆,它们都有的字符,选取其中最长的,通过循环内的代码,使得每个字符串的字符所在的位置都有一定的数值,然后把相关的,也就是我们题目所要求的,层层累加,得到最终解
#include<bits/stdc++.h>
using namespace std;
int main(){
string a,b;int i,j,p[105][105];
cin>>a>>b;
for(i=0;i<a.size();i++){
for(j=0;j<b.size();j++){
if(a[i]==b[j] )
p[i+1][j+1]=p[i][j]+1;//a字符串遍历作为外循环,b字符串遍历为内循环,对于每次a[i],如果b[j]和其相等,用下一个 p[i+1][j+1](i+1,j+1)来记录,在此i,j变量位置,加一次
else p[i+1][j+1]=max(p[i+1][j],p[i][j+1]);//否则的话取其中最大一个
}
}cout<<p[a.size()][b.size()];
return 0;
}
//动态规划算法都有一定的规律,我现在所遇到的大多都用到了双重循环,max,以数组作为统计