目录
2.2 n阶行列式
2.2.1 代数余子式和余子式
2.2.2 n阶行列式的定义
2.3 特殊行列式的计算
2.3.1 对角行列式
2.3.2 三角行列式
2.3.3 斜三角行列式
2.3.4 其他特殊行列式
2.4 行列式的性质
2.4.1 性质1
2.4.2 性质2
2.4.3 性质3
2.4.4 性质4
2.4.5 性质5
2.5 行列式的计算
2.5.1 例题1
2.5.2 例题2
2.6 克莱姆法则
2.6.1 克莱姆法则
2.6.2 克莱姆法则的证明
2.6.3 齐次线性方程组
2.7 范德蒙行列式
2.7.1 范德蒙行列式
2.7.2 范德蒙行列式的证明
2.7.3 范德蒙行列式的应用
2.8 全排列与逆序数
2.8.1 全排列
2.8.2 逆序与逆序数
2.8.3 对换
2.8.4 利用逆序数定义n阶行列式
2.9 行列式展开定理
2.9.1 行列式展开定理
2.9.2 行列式展开定理的证明
2.9.3 行列式展开定理的应用
2.2 n阶行列式
2.2.1 代数余子式和余子式
一般地,对n阶行列式,有


A为代数余子式,M为余子式
2.2.2 n阶行列式的定义
按第i行展开

按第j列展开

2.3 特殊行列式的计算
2.3.1 对角行列式

2.3.2 三角行列式


2.3.3 斜三角行列式
2.3.4 其他特殊行列式
按第一列展开,得到其



2.4 行列式的性质
2.4.1 性质1

在行列式中,行和列的位置是对称的,
对行成立的,对列也成立
2.4.2 性质2
互换两行,行列式变号

推论:
若行列式中有两行元素完全相同,则行列式为零

2.4.3 性质3
用数k乘行列式某一行中所有元素,等于用k乘此行列式

推论:某一行的所有元素的公因子可以提到行列式符号的外面
2.4.4 性质4
行列式某一行元素加上另一行对应元素的k倍,行列式的值不变

2.4.5 性质5
若行列式某一行的元素是两数之和,则行列式可拆成两个行列式的和
推论:若行列式某一行的元素都是m个元素的和,则行列式可以写成m个行列式的和
2.5 行列式的计算
2.5.1 例题1

分析:各行元素之和为一定数,故将第2、3、4全加到第1行,然后将公因子提出来

一般地,可以计算

结果为

2.5.2 例题2
结果为

2.6 克莱姆法则
2.6.1 克莱姆法则
考虑方程组

与二,三元方程组类似,n元方程组的解也可用行列式表示
若方程组的系数行列式

则方程组有惟一解

其中

2.6.2 克莱姆法则的证明
先证明
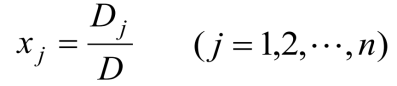
是原n元方程组的解
只需证明等式

等一共n个式子成立。我们现在只证明其中一个式子成立,其他同理。整理上式,得

这个式子可知应为某个n+1阶行列式的展开形式

再证解是惟一的
设c1、c2、...、cn为一组解

只需证

即
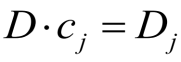
我们将第i(i≠j)列乘以ci,加到第j列,即可使得第j列为b1,b2,...,bn
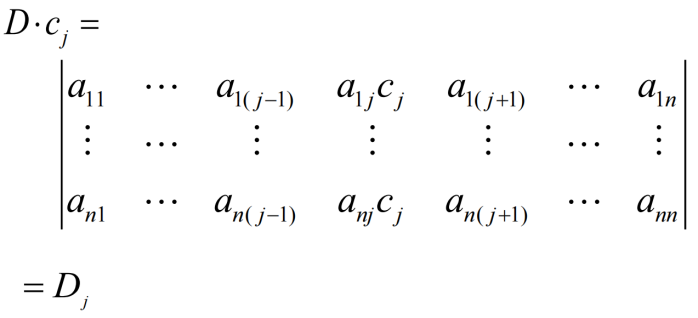
若方程组的系数行列式不为0 ,则方程组有惟一解
2.6.3 齐次线性方程组
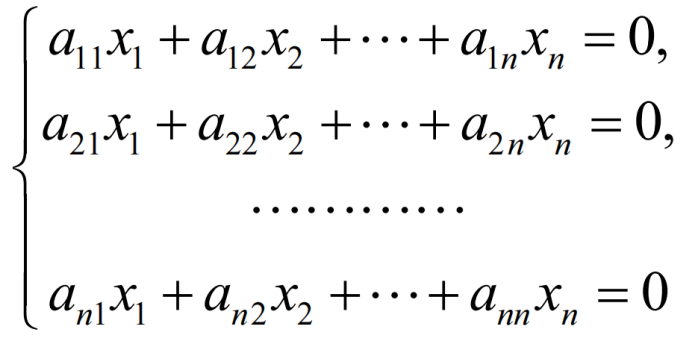
若齐次方程组的系数行列式D≠ 0 则方程组有惟一零解
例题
λ为何值时,方程组有非零解?
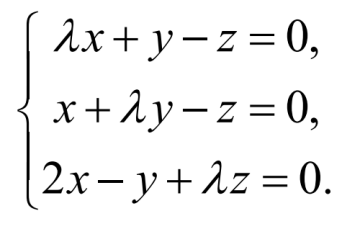
解:若方程组有非零解,则其系数行列式为零

故当 λ=1 时,方程组有非零解
2.7 范德蒙行列式
2.7.1 范德蒙行列式
按升幂排列,幂指数成等差数列

共n(n-1)/2项的乘积
结果可正可负可为零
2.7.2 范德蒙行列式的证明
归纳法证明
当k=2时

设k=n-1时公式成立,即

下证k =n时成立.
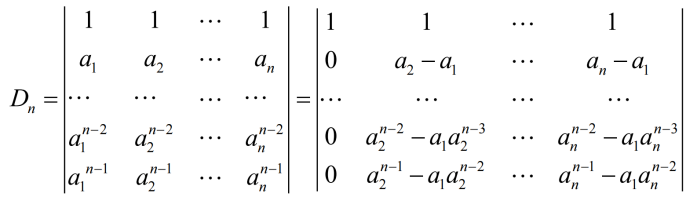

2.7.3 范德蒙行列式的应用
2.8 全排列与逆序数
2.8.1 全排列
n个不同的元素排成一列,称为n个元素的全排列。如:12345678,76532184,等等均为8个元素的全排列。
n个元素的全排列共有n!个
2.8.2 逆序与逆序数
- 全排列123 ···n称为标准排列,此时元素之间的顺序称为标准顺序。在任一排列中,若某两个元素的顺序与标准顺序不同,就称这两个元素构成了一个逆序
- 在一个排列中,逆序的总和称为逆序数。如213的逆序数为1,321的逆序数为3
- 从第一个元素起,该元素前有几个数比它大,这个元素的逆序就是几。将所有元素的逆序相加,即得到排列的逆序数
- 逆序数为奇数的排列称为奇排列,逆序数为偶数的排列称为偶排列
2.8.3 对换
在一个排列中,任意对调两个元素,其余元素不变,即得到一个新排列,这样一种变换称为对换
对换的两个性质
- 任意一个排列经一次对换后改变奇偶性
- 在n个元素的全排列中,奇偶排列各占一半,为n!/2
2.8.4 利用逆序数定义n阶行列式


2.9 行列式展开定理
2.9.1 行列式展开定理
n阶行列式D 等于它的任一行(列)各元素与其对应的代数余子式乘积之和,即

或者

2.9.2 行列式展开定理的证明
先证明以下特殊情形

我们还可以得到

下面给出一般情况的证明


2.9.3 行列式展开定理的应用
我们知道

如何求解

分两种情况讨论
若a = b,则结果为我们已知的情形
若a≠b,则
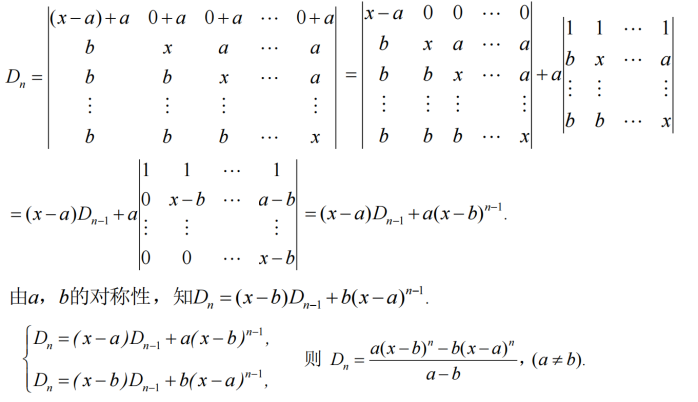








![[网络工程师]-传输层协议-UDP协议](https://img-blog.csdnimg.cn/3a0d530be29e41e4b9b824d6f98cc098.png)