PCA将相关性高的变量转变为较少的独立新变量，实现用较少的综合指标分别代表存在于各个变量中的各类信息，既减少高维数据的变量维度，又尽量降低原变量数据包含信息的损失程度，是一种典型的数据降维方法。PCA保留了高维数据最重要的一部分特征，去除了数据集中的噪声和不重要特征，这种方法在承受一定范围内的信息损失的情况下节省了大量时间和资源，是一种应用广泛的数据预处理方法。

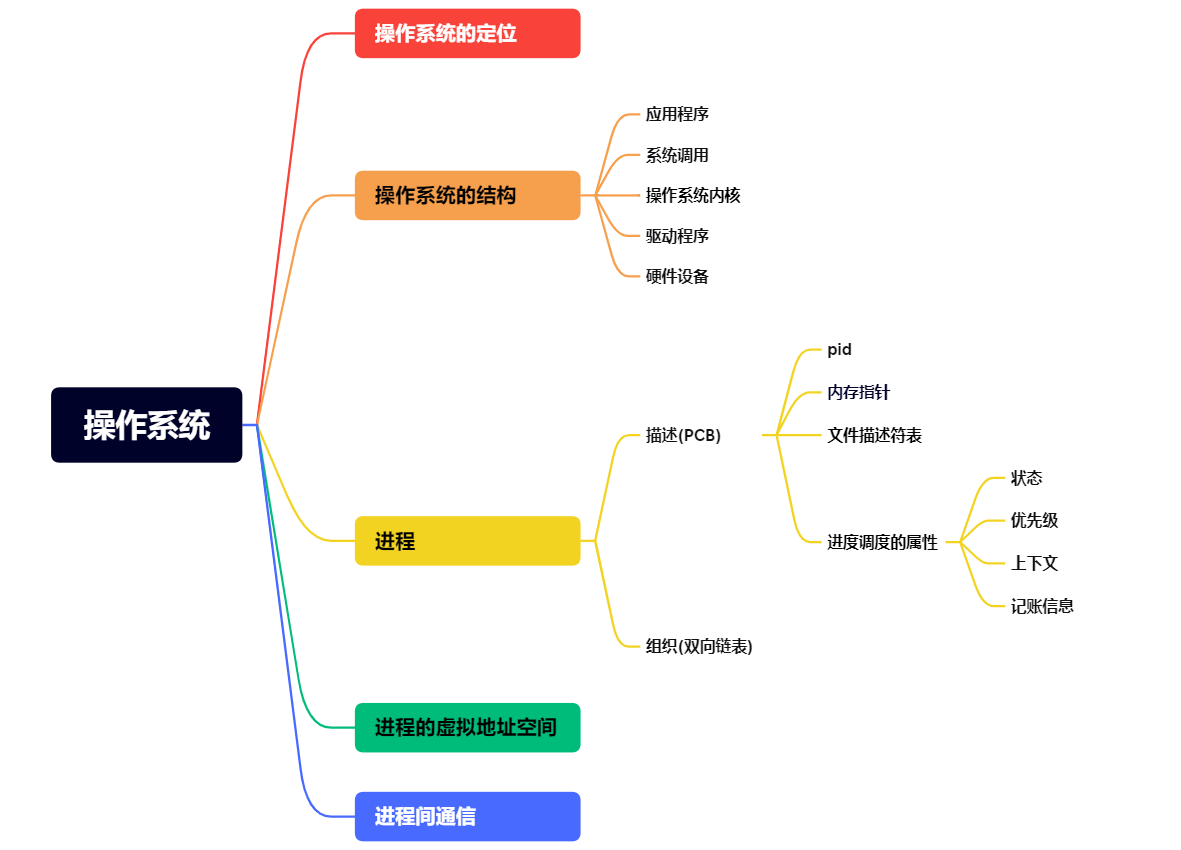
PCA在数据挖掘和机器学习实践中的应用主要集中于几个方面，如图5-1所示。

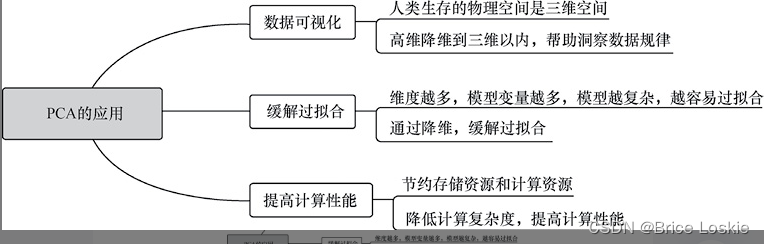
 （1）数据可视化。人类生存的物理空间是三维空间，任何高于三维的数据我们都无法通过视觉直接感知。因此，数据科学家常常使用PCA对高维数据进行降维，从而便于可视化地展示数据特点，帮助研究人员洞察数据中蕴含的规律。

（2）缓解过拟合。机器学习中数据维度越多就意味着模型的变量越多，也就意味着模型的复杂度越高。越高的模型复杂度越容易导致过拟合。因此，机器学习中通过PCA对训练数据进行降维处理，能够在一定程度上缓解过拟合。

（3）提高计算性能。高维数据不仅占用过多的存储资源，而且由于维度较高导致计算的复杂度不断上升。例如一张长32像素点、宽32像素点的人脸或者手写数字的图像，它的向量的维度可以达到32×32=1 024。这会导致庞大的存储量和计算量，并造成存储资源和计算资源的巨大开销。因此，通过PCA进行降维处理可以节约存储资源和计算资源，提高计算性能。

假设我们收集到某班级5名同学的各科成绩，如表

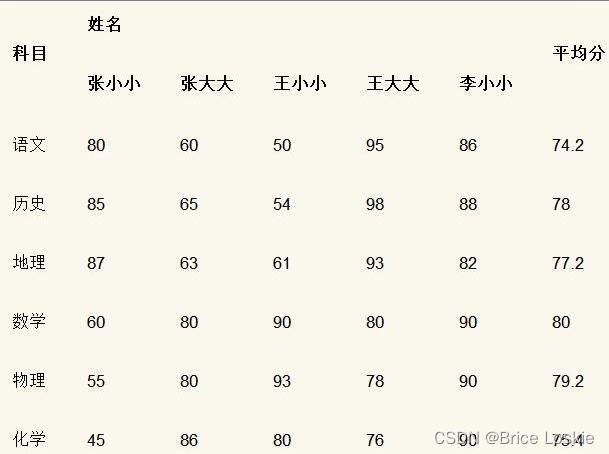
 为了便于后续计算展示，我们采用特征维度零均值化方式（所有科目成绩减去该科目所有学生成绩平均值）来处理数据，如表

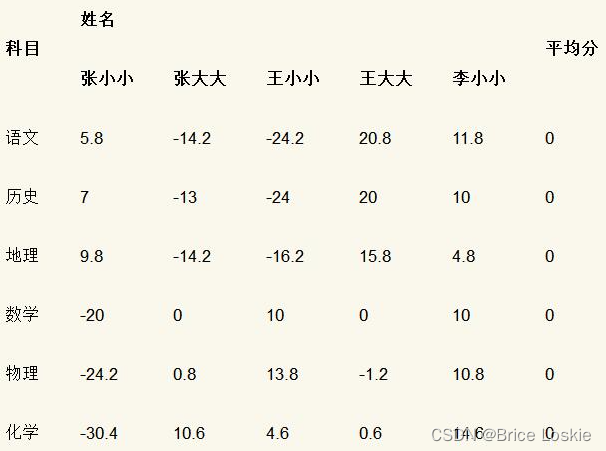
 我们首先将上述经过零均值化处理的数据写成矩阵形式，如下所示。

        我们发现，上面矩阵为6行5列。其中，每一列表示一名学生的成绩，每一行表示一个维度（如语文、历史、地理、数学、物理、化学）。例如第一列表示的是姓名为“张小小”的学生各科成绩经过零均值化后的结果。

经过零均值化的数据预处理后，我们就可以正式开启PCA过程了，步骤如下。

（1）计算协方差矩阵。

计算矩阵A的6个行向量（如语文、历史、地理、数学、物理、化学）的协方差矩阵

 （2）计算特征值与特征向量。

上述协方差矩阵C的特征值为 

         假设我们现在需要将原矩阵A（6维，即6个行向量）降为2维矩阵，那么我们可以选择最大的两个特征值830.701、399.845。这样，我们就可以得到对应的特征值与特征向量。

第一，特征值为830.701时，对应的特征向量为

第二，特征值为399.845时，对应的特征向量为

 

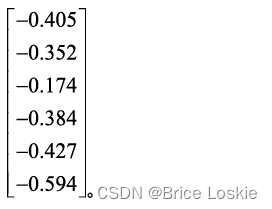
 （3）矩阵相乘实现降维。

上面选择的特征向量就是我们降维后新空间的基，将其作为行向量形成2×6的矩阵P，如：

 然后，再将矩阵P与矩阵A相乘，就可以实现降维。

 

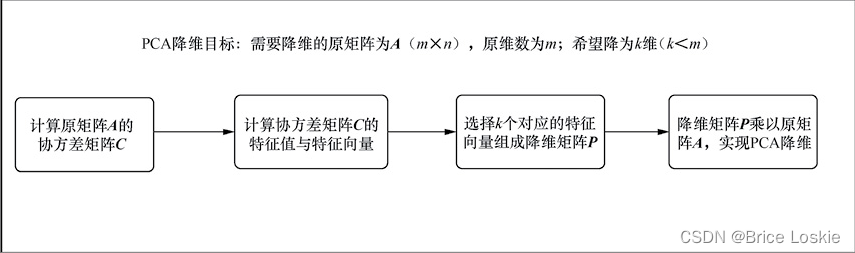
所以，PCA过程包含以下几个步骤，如图5-2所示。