信号的变换
在实践中,缩放和时间平移是遇到的两个最重要的信号变换。缩放改变了振幅轴上的因变量的值,而时间平移则影响了时间轴上的自变量的值。
加法
对于两个离散时间信号的加法,例如 x [ n ] x[n] x[n] 和 y [ n ] y[n] y[n],逐样本相加这两个信号的每个值:
z [ n ] = x [ n ] + y [ n ] 对所有 n 适用 z[n] = x[n] + y[n] \quad \text{对所有} \ n \ 适用 z[n]=x[n]+y[n]对所有 n 适用
例如:
z [ 0 ] = x [ 0 ] + y [ 0 ] z[0] = x[0] + y[0] z[0]=x[0]+y[0]
z [ 1 ] = x [ 1 ] + y [ 1 ] z[1] = x[1] + y[1] z[1]=x[1]+y[1]
以此类推。
乘法
对于乘法,像我们在加法中所做的那样,将两个信号逐样本相乘:
z
[
n
]
=
x
[
n
]
⋅
y
[
n
]
z[n] = x[n] \cdot y[n]
z[n]=x[n]⋅y[n] 对于每一个
n
n
n,
例如:
z [ 0 ] = x [ 0 ] ⋅ y [ 0 ] z[0] = x[0] \cdot y[0] z[0]=x[0]⋅y[0]
z [ 1 ] = x [ 1 ] ⋅ y [ 1 ] z[1] = x[1] \cdot y[1] z[1]=x[1]⋅y[1]
...等等。
Tips:加法乘法最容易理解。
缩放
缩放意味着将信号的幅度乘以一个常数 α \alpha α,得到 α ⋅ s [ n ] \alpha \cdot s[n] α⋅s[n],其中 α \alpha α 可以是正数、负数、大于或小于1的数。例如,图1.13显示了信号 s [ n ] s[n] s[n] 缩放了4倍(比较两个信号在y轴上的幅度)。需要注意的是,缩放时,整个信号都会被相同的值缩放,因此缩放与两个信号逐样本相乘不同。
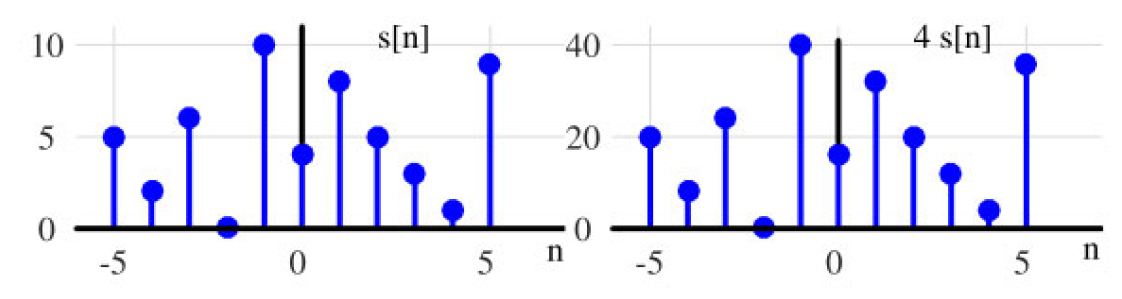
图 将s[n]放大四倍
接下来上难度:
时间平移
信号 s [ n ] s[n] s[n] 可以向右或向左移动任意 m m m 个单位。有两种方式来理解时间平移信号。
常规方法 - 平移信号
平移离散时间信号通常描述如下:
延迟: 对于 s [ n − m ] s[n - m] s[n−m],时间平移会导致 s [ n ] s[n] s[n] 延迟 m m m 个时间单位。所以通过将 s [ n ] s[n] s[n] 向右平移 m m m 个单位来绘制 s [ n − 2 ] s[n - 2] s[n−2](图a)。
提前: 对于 s [ n + m ] s[n + m] s[n+m],时间平移会导致 s [ n ] s[n] s[n] 提前 m m m 个时间单位。所以通过将 s [ n ] s[n] s[n] 向左平移 m m m 个单位来绘制 s [ n + 2 ] s[n + 2] s[n+2](图a)。
这很容易记住:将时间平移写作 n − m n - m n−m。向右平移 s [ n − m ] s[n - m] s[n−m],向左平移 s [ n + m ] s[n + m] s[n+m]。
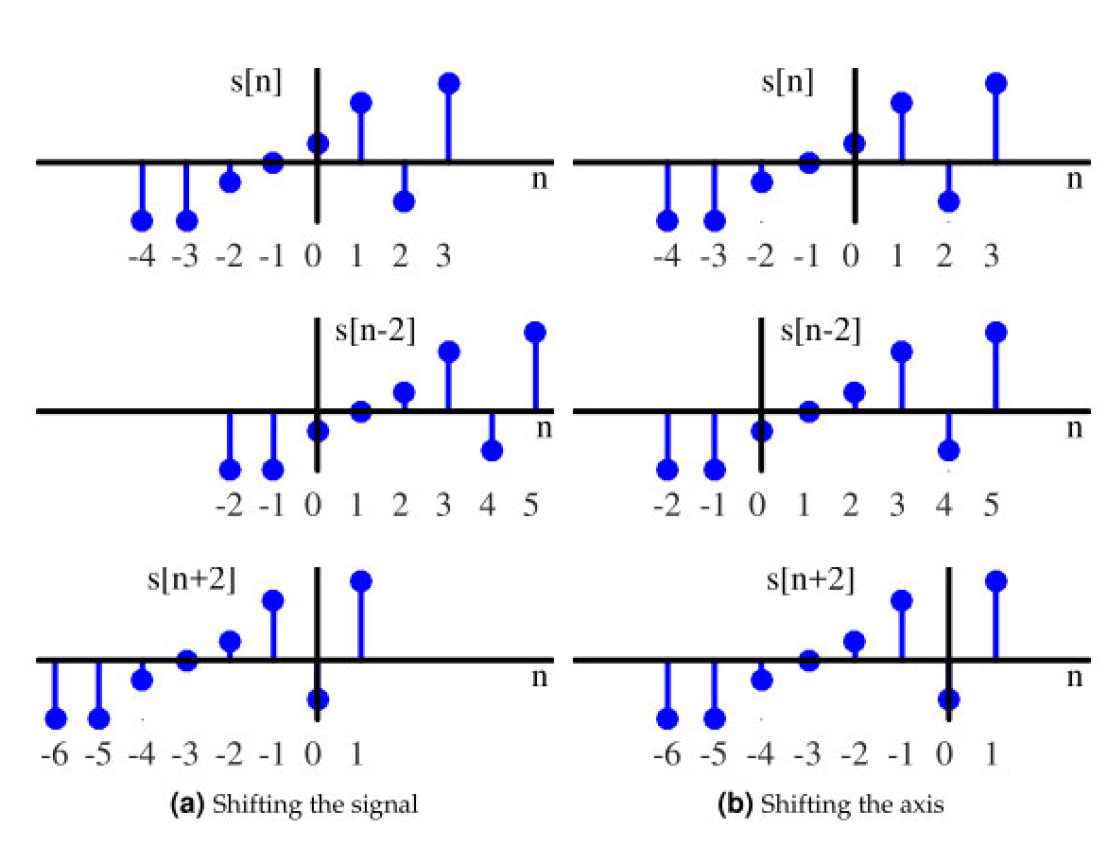
图 :两种观察时间平移信号的方法
直观方法 - 平移坐标轴
在信号处理应用中,“此刻”是时间索引 0,我们希望将其作为信号生命的主要焦点,如图所示。从这个角度看:
延迟: 对于 s [ n − m ] s[n - m] s[n−m], n − m n - m n−m 显然意味着向过去移动 m m m 个单位。因此,通过回溯 2 个单位并将其设为新的“此刻”,即时间索引 0,来绘制 s [ n − 2 ] s[n - 2] s[n−2](图b)。
提前: 对于 s [ n + m ] s[n + m] s[n+m], n + m n + m n+m 显然意味着向未来前进 m m m 个单位。因此,通过向未来移动 2 个单位并将其设为新的“此刻”,即时间索引 0,来绘制 s [ n + 2 ] s[n + 2] s[n+2](图b)。

图 1.15:信号的过去、现在和未来
换句话说,只需观察时间轴本身。保持离散时间信号不变,但将时间索引 0 移动 m m m 个单位到左侧,对应 n − m n - m n−m,并将 m m m 个单位移动到右侧,对应 n + m n + m n+m,如图 b 所示。注意, s [ n + 2 ] s[n+2] s[n+2] 的索引 0 与 s [ n ] s[n] s[n] 的索引 2 位于同一采样点,表示访问未来值。虽然这仅仅是观察过程的不同方式,但这是一种更简单、更直观的方法。这种方法对于卷积的理解会非常有用。
注释 1.2 时间平移信号的叠加
理解时间平移信号可以轻松分析看似复杂的方程式,例如:
r [ n ] = ∑ m = − 1 2 s [ n − m ] r[n] = \sum_{m=-1}^{2} s[n-m] r[n]=∑m=−12s[n−m]
这基本上是将 s [ n − m ] s[n-m] s[n−m] 在 m = − 1 , 0 , 1 , 2 m = -1, 0, 1, 2 m=−1,0,1,2 的情况下叠加在一起。我们可以通过替换 m m m 的值将其简化为更易识别的形式:
r [ n ] = s [ n + 1 ] + s [ n ] + s [ n − 1 ] + s [ n − 2 ] r[n] = s[n+1] + s[n] + s[n-1] + s[n-2] r[n]=s[n+1]+s[n]+s[n−1]+s[n−2]
现在,我们可以轻松绘制 s [ n ] s[n] s[n] 的时间平移版本,并将它们叠加在一起,找到最终的信号。例如,图显示了单位脉冲信号 δ [ n ] \delta[n] δ[n] 及其时间平移版本。
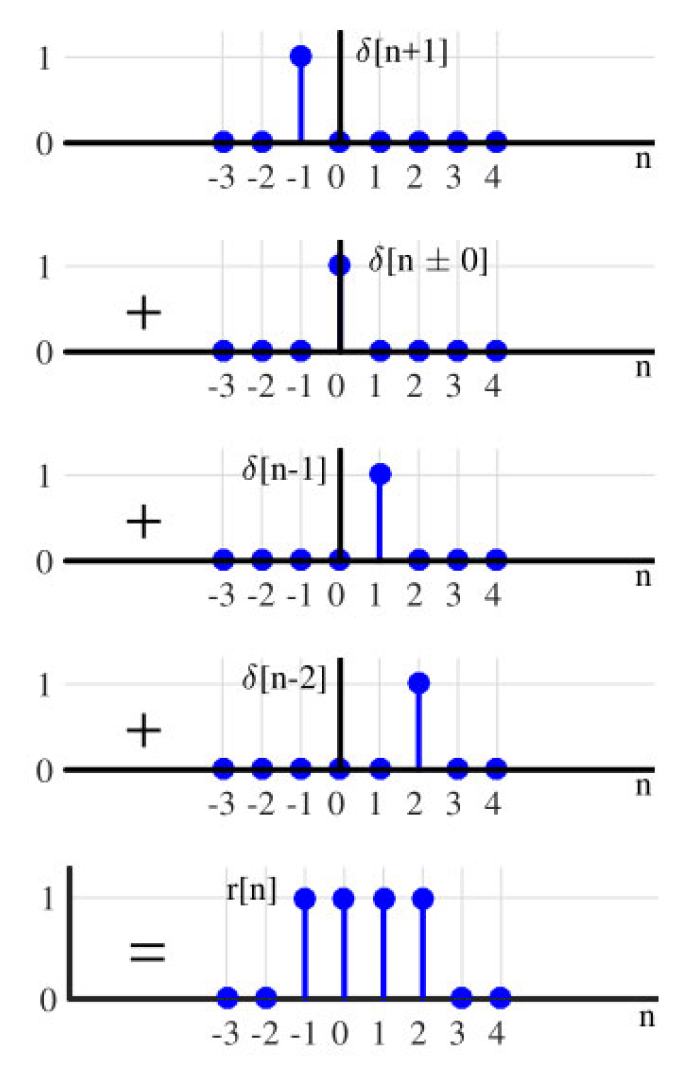
图 :计算 r [ n ] = ∑ m = − 1 2 s [ n − m ] r[n] = \sum_{m=-1}^{2} s[n-m] r[n]=∑m=−12s[n−m] 对于 s [ n ] = δ [ n ] s[n] = \delta[n] s[n]=δ[n]
翻转或时间反转
当自变量 n n n 被替换为 − n -n −n 时,信号会围绕时间原点 n = 0 n = 0 n=0 反射或翻转,因为 n = + 1 n = +1 n=+1 处的采样点会移到 n = − 1 n = -1 n=−1 处, n = − 5 n = -5 n=−5 处的采样点会移到 n = + 5 n = +5 n=+5 处,依此类推。通过绘制 s [ − n ] s[-n] s[−n] 和 s [ − n + 3 ] s[-n+3] s[−n+3] 来说明这一概念。
注意,由于时间轴 − n -n −n 的翻转,向左或向右平移的规则也会变得相反。例如,从直观方法来看,时间轴 n n n 被替换为 − n -n −n 表示过去变成未来,因此, s [ − n + 3 ] s[-n+3] s[−n+3] 首先将信号围绕时间原点翻转,然后向左移动 3 个单位至过去,将其标记为新的“现在”(时间索引 0)。

图 1.17:翻转和时间移位信号
循环移位
循环移位与信号的时间移位非常相似,不同之处在于只关注一个长度为 N N N 的采样段进行循环移位,而常规时间移位的可用轴范围是从 − ∞ -\infty −∞ 到 + ∞ +\infty +∞。
如果一个信号 s [ n ] s[n] s[n] 向右循环移位 m m m 个单位,那么那些从长度为 N N N 的段右侧“掉下去”的信号 s [ n ] s[n] s[n] 的采样点会重新出现在段的起始位置。同样,如果 s [ n ] s[n] s[n] 向左循环移位 m m m 个单位,那么从长度为 N N N 的段左侧“掉下去”的信号 s [ n ] s[n] s[n] 的采样点会重新出现在段的末尾。就像视频游戏中的角色一样,它在屏幕的一端消失后会从另一端重新出现。图显示了一个向右循环移位的例子。
方法 1
由于循环移位是针对长度为 N N N 的段进行的,因此移位是按模 N N N 计算的,并表示为 s [ ( n − m ) m o d N ] s[(n-m) \mod N] s[(n−m)modN],其中 ( n − m ) m o d N (n-m) \mod N (n−m)modN 表示进行移位。

图 :在游戏轴上吃豆人向右循环移位
- 信号 s [ ( n − 1 ) m o d 8 ] s[(n-1) \mod 8] s[(n−1)mod8] 对每个样本右移1位,除了时间索引7的样本。这个样本不会移到索引8,而是从左侧回到索引0。
- 同样地,信号 s [ ( n + 3 ) m o d 8 ] s[(n+3) \mod 8] s[(n+3)mod8] 对大多数样本左移3位,除了时间索引0、1和2的样本。它们不会移动到负时间索引,而是从右侧回到索引5、6和7。

图 :信号 s [ ( n − m ) m o d 8 ] s[(n-m) \mod 8] s[(n−m)mod8] 的循环移位
方法 2
首先,观察图中的绿色虚线样本。请注意,信号 s [ n ] s[n] s[n] 在两侧重复以使其成为周期性的,这样原始索引为 n = 5 n=5 n=5, 6 6 6 和 7 7 7 的样本会出现在索引 n = 0 n=0 n=0 之前,而原始索引为 n = 0 n=0 n=0 和 1 1 1 的样本会出现在 n = 7 n=7 n=7 之后。在这种情况下,循环移位就像常规移位一样。将上图的信号按1位右移,即 s [ n − 1 ] s[n-1] s[n−1],可以看到结果是图中间显示的 s [ ( n − 1 ) m o d 8 ] s[(n-1) \mod 8] s[(n−1)mod8]。
循环翻转
在这个阶段,一个有趣的问题是:循环翻转信号 s [ ( − n ) m o d N ] s[(-n) \mod N] s[(−n)modN] 的结果是什么?
循环移位的逻辑保持不变。与常规翻转一样,索引为0的样本保持不变。根据上面方法1,索引7的样本应位于 − 7 -7 −7 处,但循环表示法中没有负索引,因此 ( − 7 ) m o d 8 = − 7 + 8 = 1 (-7) \mod 8 = -7 + 8 = 1 (−7)mod8=−7+8=1,这使其移至索引1。图显示了相同信号 s [ ( − n ) m o d N ] = s [ − n + N ] s[(-n) \mod N] = s[-n+N] s[(−n)modN]=s[−n+N] 的结果。
根据方法2,并考虑图中的绿色虚线样本,常规翻转意味着索引0左侧的三个样本现在出现在图中索引0右侧。
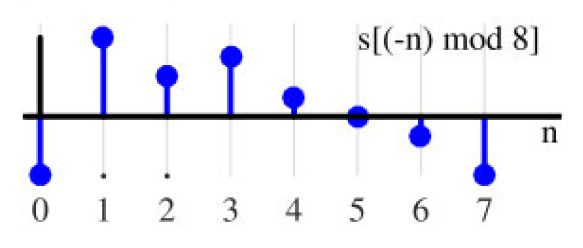
图 循环翻转
Tips:离散傅里叶变换打基础,要花时间去理解。