自抗扰控制ADRC原理解析及案例应用

1. ADRC基本原理

1.1 ADRC的基本概念

自抗扰控制（Active Disturbance Rejection Control，ADRC）是一种先进的控制策略，由韩京清研究员于1998年提出。ADRC的核心思想是将系统内部和外部的不确定性因素视为总扰动，并通过扩张状态观测器（Extended State Observer，ESO）对其进行估计和补偿。这种方法不依赖于被控对象的精确数学模型，使得ADRC在处理非线性、时变以及存在未知扰动的复杂系统控制中表现出色。

ADRC的基本结构包括三个主要部分：跟踪微分器（Tracking Differentiator，TD）、扩张状态观测器（ESO）和非线性状态误差反馈控制律（Nonlinear State Error Feedback，NLSEF）。TD用于提取系统输入的连续信号和微分信号；ESO用于估计系统状态和总扰动；NLSEF则根据ESO的输出来设计控制律，实现对系统状态的精确控制。

1.2 ADRC的发展历史

自抗扰控制技术自提出以来，经历了从理论探索到工程应用的逐步发展。最初，ADRC主要在学术界进行研究，随着对其理论的深入理解和技术的进步，ADRC开始被应用于各种工业和工程领域。例如，在电机控制、机器人技术、汽车悬挂系统以及飞行控制系统中，ADRC都展现出了其卓越的控制性能。

随着计算机技术的发展，ADRC的实现变得更加高效和便捷。现代的ADRC控制器可以很容易地集成到各种控制系统中，提供实时的扰动估计和补偿。此外，ADRC的参数整定相对简单，通常只需要调整一个参数——带宽，这大大简化了控制器的设计和调试过程。

ADRC的另一个重要发展方向是与其他控制策略的融合，如模糊控制、神经网络和自适应控制等，以进一步提高系统的鲁棒性和适应性。这些融合策略不仅拓宽了ADRC的应用范围，也提高了其在复杂环境下的性能表现。

2. ADRC的工作原理

2.1 扩张状态观测器ESO

扩张状态观测器（Extended State Observer，ESO）是ADRC中的关键组件之一。ESO的主要任务是估计系统状态和总扰动。在ADRC中，总扰动被视为系统状态的一部分，与系统状态一起被观测和估计。ESO的设计通常基于系统动态方程的线性化或近似模型，其输出包括系统状态的估计值和总扰动的估计值。

ESO的一般形式可以表示为：

$\dot{\hat{x_{1}}}=\dot{\hat{x_{2}}}$

$\dot{\hat{x_{2}}}=\dot{\hat{x_{3}}}+l_{1}(y-\dot{\hat{x_{1}}})$

$\dot{\hat{x_{3}}}=-l_{2}\dot{\hat{x_{3}}}+l_{1}y$

其中， $\dot{\hat{x_{1}}}$ 、 $\dot{\hat{x_{2}}}$ 和 $\dot{\hat{x_{3}}}$ 分别是系统状态和总扰动的估计值， $y$ 是系统的测量输出， $l_{1}$ 和 $l_{2}$ 是ESO的参数。

2.2 跟踪微分器TD

跟踪微分器（Tracking Differentiator，TD）用于生成跟踪信号及其微分信号。TD的设计目的是解决传统微分器在处理不连续或带噪声的测量信号时的问题。TD能够提供一个连续且无噪声的信号，同时保持对阶跃输入的快速响应。

TD的数学表达式为：

$TD(u(t),y(t),v(t))=\begin{bmatrix} v(t)\\ \dot{v(t)} \end{bmatrix}$

其中， $u(t)$ 是控制输入， $y(t)$ 是系统输出， $v(t)$ 是TD的输出，表示跟踪信号，而 $\dot{v(t)}$ 是 $v(t)$ 的导数，即跟踪信号的微分。

2.3 非线性状态误差反馈控制律NLSEF

非线性状态误差反馈控制律（Nonlinear State Error Feedback，NLSEF）是ADRC的最后一个环节，负责根据ESO和TD提供的信息生成控制信号。NLSEF的设计通常基于最速控制理论或非线性控制理论，以实现对系统状态的快速且精确的控制。

NLSEF的控制律可以表示为：

$u(t)=-k_{1}e(t)-k_{2}\dot{e(t)}-k_{3}e^{\alpha }(t)$

其中， $e(t)$ 是系统输出与期望输出之间的误差， $\dot{e(t)}$ 是误差的导数， $k_{1}$ 、 $k_{2}$ 和 $k_{3}$ 是控制律的参数， $\alpha$ 是非线性项的指数，用于增强控制律的鲁棒性。

3. ADRC的参数设计

3.1 参数整定方法

参数整定是ADRC应用中的关键步骤，它直接影响到控制效果和系统稳定性。ADRC的参数主要包括扩张状态观测器（ESO）的参数和非线性状态误差反馈控制律（NLSEF）的参数。

扩张状态观测器（ESO）参数：ESO的参数决定了对系统状态和扰动的估计精度。参数设计需要考虑观测器的收敛速度和对噪声的抑制能力。一般而言，较大的观测器增益可以加快收敛速度，但同时也可能放大噪声的影响。
非线性状态误差反馈控制律（NLSEF）参数：NLSEF的参数设计涉及到控制律的非线性特性，这些特性可以提供更好的鲁棒性和适应性。参数设计需要平衡系统的超调、稳定性和响应速度。

参数整定方法通常包括基于经验的调整、基于模型的优化以及基于仿真的迭代优化等。在实际应用中，参数整定往往需要结合系统特性和控制需求进行多次调整和验证。

3.2 参数对系统性能的影响

参数的选择对ADRC控制系统的性能有着显著的影响。

收敛速度：参数设置可以影响系统达到稳态所需的时间。较大的ESO增益可以加快收敛速度，但过大可能导致系统过冲。
超调与稳定性：NLSEF的参数可以调整系统的超调量和稳定性。适当的参数设置可以减少超调，提高系统的稳定性。
鲁棒性：ADRC的参数设计需要考虑到系统的不确定性和外部扰动。合理的参数可以提高系统对这些不确定性的抵抗能力。
适应性：参数的调整可以提高系统对参数变化和操作条件变化的适应性，确保在不同工况下都能保持良好的控制效果。

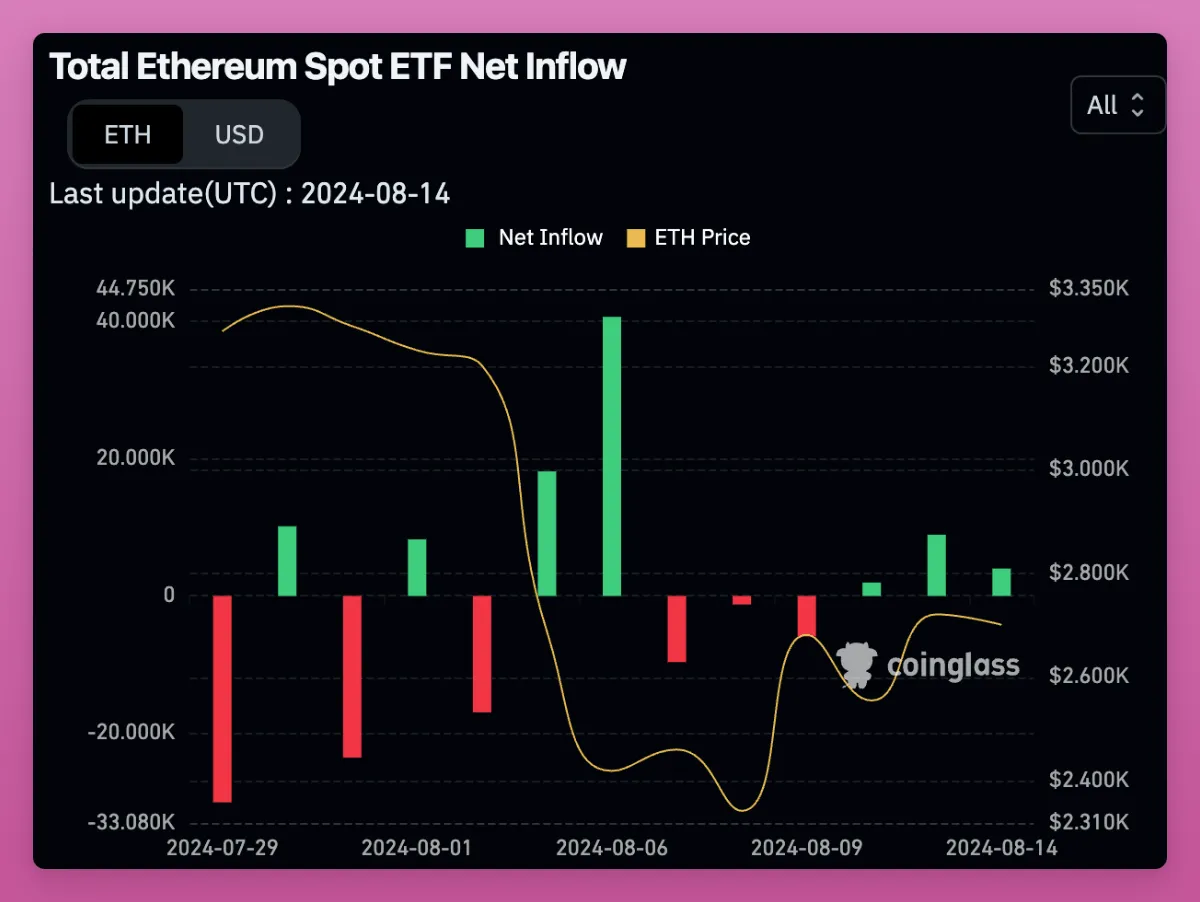
车道保持辅助系统（LKAS）的ADRC实例

自抗扰控制（ADRC）可以应用于自动驾驶汽车的某些控制问题，例如车道保持辅助系统（Lane Keeping Assist System, LKAS）。以下是一个ADRC应用于车道保持辅助系统的例子。假设自动驾驶汽车的横向控制模型可以简化为一个二阶系统，用于描述车辆相对于车道中心的横向位置 $y$ 和横向速度 $\dot{y}$ 的动态行为：

$m\ddot{y}+b\dot{y}+ky=u$

其中：

$m$ 是车辆的质量
$b$ 是与横向速度相关的阻尼系数
$k$ 是与横向位置相关的弹性系数
$u$ 是控制输入，可以是转向角或转向力矩

ADRC控制器的目标是使车辆的横向位置 $y$ 跟踪车道中心线。

ADRC控制器设计

扩张状态观测器（ESO）: 用来估计车辆的横向位置 $y$ 和横向速度 $\dot{y}$ ，以及总扰动 $d$ ：

$\dot{\hat{y}}=\hat{\dot{y}}+\hat{d}$

$\hat{\dot{y}}=-\frac{a_{1}}{m}(\hat{y}-y_{ref})-\frac{a_{2}}{m}\hat{\dot{y_{2}}}+\frac{1}{m}u$

其中， $y_{ref}$ 是车道中心线的参考位置。

非线性状态误差反馈控制律(NLSEF):

$u=k_{p}(\hat{y}-y_{ref})+k_{i}\int (\hat{y}-y_{ref})dt+k_{d}(\hat{\dot{y}}-\dot{y_{ref}})$

其中， $k_{p}$ ， $k_{i}$ ， $k_{d}$ 是控制增益， $\dot{y_{ref}}$ 是车道中心线的参考横向速度。

总扰动估计器:

$\dot{\hat{d}}=-\frac{a_{3}}{m}(\hat{y}-{y_{ref}})$

其中， $a_{3}$ 是估计器参数。

C++代码示例

#include <iostream>
#include <cmath>

// 系统参数
const double m = 1500; // 车辆质量，单位：kg
const double b = 100; // 阻尼系数，单位：Ns/m
const double k = 20000; // 弹性系数，单位：N/m
const double a1 = 30; // ESO参数
const double a2 = 5; // ESO参数
const double a3 = 10; // 总扰动估计器参数

// 控制参数
const double kp = 1; // 比例增益
const double ki = 0.1; // 积分增益
const double kd = 0.5; // 微分增益

// 初始状态
double y = 0; // 横向位置
double y_dot = 0; // 横向速度
double y_hat = 0; // 横向位置估计
double y_dot_hat = 0; // 横向速度估计
double d_hat = 0; // 总扰动估计

// 参考轨迹
double y_ref = 0; // 车道中心线的参考位置

// 时间参数
const double dt = 0.01; // 时间步长，单位：s
double t = 0; // 当前时间

// 模拟函数
void simulateADRC() {
    while (true) {
        t += dt;

        // 更新估计值
        y_dot_hat += (-a1 * (y_hat - y_ref) - a2 * y_dot_hat + u / m) * dt;
        y_hat += y_dot_hat * dt;
        d_hat += (-a3 * (y_hat - y_ref)) * dt;

        // 计算控制输入
        double u = kp * (y_hat - y_ref) + ki * (y_hat - y_ref) * dt + kd * (y_dot_hat - 0); // 假设车道中心线速度为0

        // 输出当前状态和控制输入
        std::cout << "Time: " << t << ", y: " << y << ", y_dot: " << y_dot << ", u: " << u << std::endl;

        // 更新车辆的横向位置和速度（这里简化处理，假设车辆响应控制输入）
        y += y_dot * dt;
        y_dot += (u - b * y_dot - k * y) / m * dt;

        // 检查是否达到模拟时间
        if (t > 10) break;
    }
}

int main() {
    simulateADRC();
    return 0;
}