8.12 day bug
news2026/2/13 6:42:31
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/2033585.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
数据库方式实现实时排行榜
文章目录 🌞 Sun Frame:SpringBoot 的轻量级开发框架(个人开源项目推荐)🌟 亮点功能📦 spring cloud模块概览常用工具 🔗 更多信息1.排行榜的设计1.实时榜单1.数据库统计2.redis 的 sorted set …
25届秋招还有金九银十?会是“史上最难”?
吉祥学安全:知星🔗http://mp.weixin.qq.com/s?__bizMzkwNjY1Mzc0Nw&mid2247483727&idx1&sndb05d8c1115a4539716eddd9fde4e5c9&chksmc0e47813f793f105017fb8551c9b996dc7782987e19efb166ab665f44ca6d900210e6c4c0281&scene21#wechat…
笔记(day17)集合概述、List、Set、比较器
集合Collection
一.概述
集合可以理解为数据结构的封装,根据不同的特性及操作性能进行分类
二.继承体系 三.Collection中常用方法
collection是集合中的父类,所以collection中的方法是所有集合中都有的 集合中只能保存引用类型(Object),无法保存基本类型 Colle…
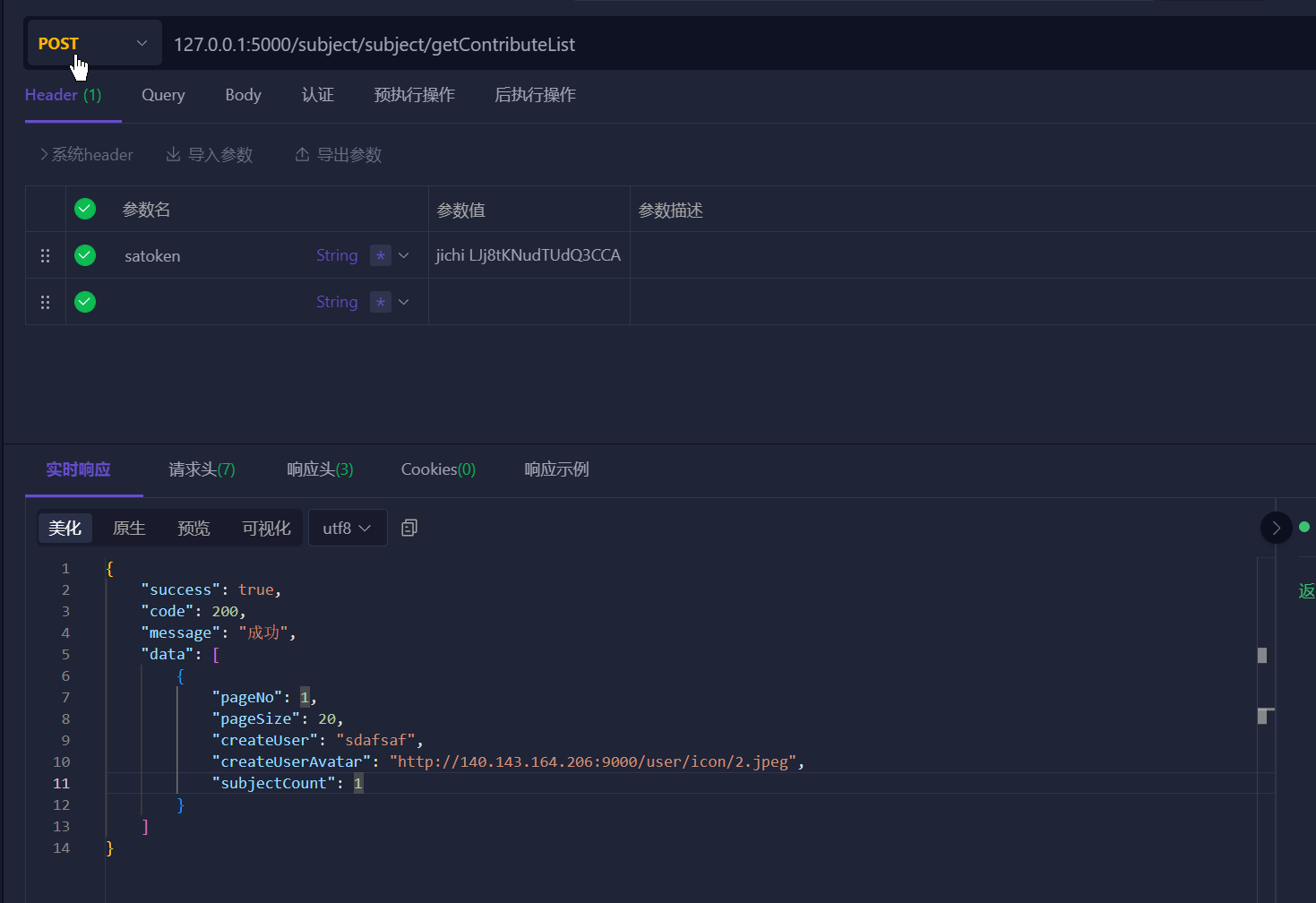
记一次CSDN认证模块后端未校验漏洞
前言
作为一个程序员,一直充满好奇心,没事就喜欢找找漏洞,试想一下某些程序是否存在某些鉴权等漏洞,目前该漏洞已提交官方,且影响不大,现分享分析过程用于各位技术学习。
漏洞分析
https://i.csdn.net/#…
【Hot100】LeetCode—3. 无重复字符的最长子串
目录 1- 思路滑动窗口 2- 实现⭐3. 无重复字符的最长子串——题解思路 3- ACM 实现 原题链接:3. 无重复字符的最长子串 1- 思路
滑动窗口
借助 HashSet 来实现判重通过指针 i 和 right 指针实现一个滑动窗口 2- 实现
⭐3. 无重复字符的最长子串——题解思路 clas…
webrtc一对一视频通话功能实现
项目效果 实现原理
关于原理我就不做说明,直接看图 WebRTC建立的时序图
系统用例逻辑 搭建环境
turn服务器:Ubuntu24.04搭建turn服务器 mkcert的安装和使用:配置https访问 必须使用https协议, 由于浏览器的安全策略导致的&am…
图像处理中的图像梯度和幅值是什么???(通俗讲解)
在边缘检测和特征提取等任务中,图像的梯度和幅值是图像处理中非常重要的概念。 目录 一、图像的梯度1.1 专业解释1.2 通俗理解1.3 计算方式 二、梯度的幅值2.1 专业解释2.2 通俗理解2.3 计算方式 一、图像的梯度
1.1 专业解释
图像的梯度可以看作是图像中亮度或颜…
基于智能手机的3D模型快速生成技术
摘要: 本文介绍了一种创新技术,该技术允许用户通过智能手机拍摄视频,快速将2D图像转换为3D模型。这项技术为3D内容创作提供了一种高效且用户友好的解决方案。
关键词: 3D建模,智能手机,AI处理,…
【递归】1.汉诺塔问题
面试题 08.06. 汉诺塔问题
leetcode链接:https://leetcode.cn/problems/hanota-lcci/description/在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。
一开始,所有盘子自上而下按升序依次套在第…
WMS如何实现与TMS的双向信息流?
要实现仓储管理系统(WMS)与运输管理系统(TMS)之间的双向信息流,可以通过以下几个步骤进行集成:
——————————————————
1、需求分析: 1):确定WMS和TMS之间需要传输的数据类型&…
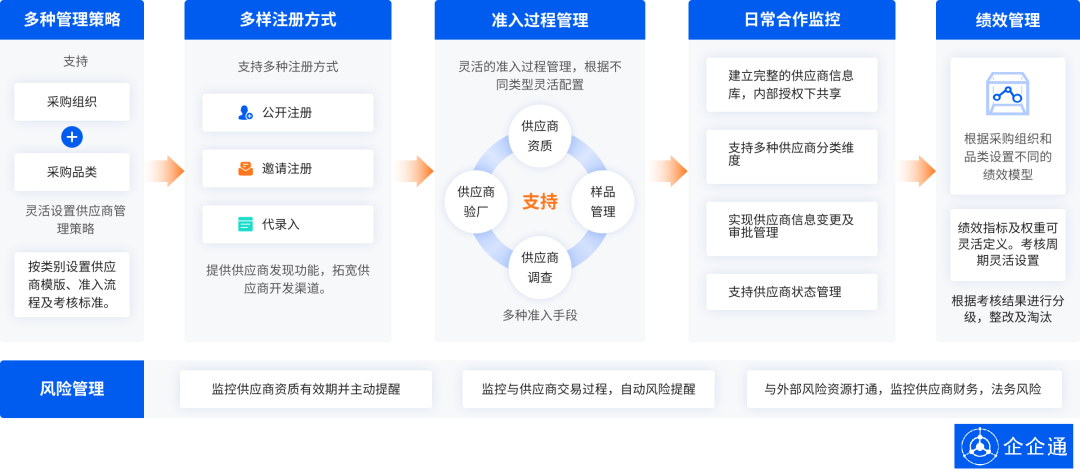
“小巨人”『南斗六星』×企企通,携手推动华中地区智能网联企业供应链数字化发展
近日,湖北省知名“小巨人”企业——南斗六星系统集成有限公司(以下简称“南斗六星”)与企企通达成合作,并成功召开数字化建设项目启动会议。 由南斗六星总经理带头的各部门骨干,以及企企通华中区负责人、项目负责人等一…
小白零基础学数学建模应用系列(二):基于Python的共享单车系统建模与仿真分析
共享单车系统作为一种绿色环保的出行方式,已成为现代城市公共交通的重要组成部分。本文将使用Python编程语言,并结合modsim库,构建并仿真一个共享单车系统的模型,通过这一过程来展示如何进行系统的建模与分析。 文章目录 一、背景…
大厂面试题分享第二期
大厂面试题分享第二期 如果执行了一条命令,"select count(*)from…",使用哪个引擎更快,为什么?垃圾回收器 CMS 和 G1的区别介绍一下CMS和G1CMS(并发)垃圾收集器G1垃圾回收器 HTTPS和HTTP的区别主…
网站谷歌SEO优化要注意什么?
就最近我们接触的客户而言,有不少客户连最基本的seo常识都没有,他们固然可能是技术大咖,但如果你还是期望从谷歌seo获取流量,那么,最基本的源代码输出必须要有,正常情况下,整个页面除了动画交互…
windows10和linux(debian12)设置静态ip————附带详细过程
文章目录 0 背景1 linux(debian)1.1 查看网络配置1.2 获取ip动态分配下的配置1.3 打开网络配置文件1.4 重新启动网络服务1.5 验证设置 2 windows2.1 查看自动获取ip地址下的配置2.2 进行设置 0 背景
因为下位机只能获取固定的ip(ip池很小&am…
递归 与 dfs 综合练习(一)
目录 一、找出所有子集的异或总和再求和
1.题目链接:1863. 找出所有子集的异或总和再求和
2.题目描述:
3.解法(递归)
🌵算法思路:
🌵算法代码:
二、全排列 II
1.题目链接&…
“低代码技术:数字化工厂的加速器与智能制造的桥梁“
引言
随着工业4.0和智能制造的快速发展,数字化工厂成为了现代制造业的核心概念。这一转型不仅依赖于物联网、人工智能、大数据等新兴技术,也需要软件开发的支持。然而,传统的软件开发模式由于其复杂性和周期长,难以快速适应数字化…
案例-华东某财险公司:引入监控易一体化运维软件
在华东这片经济活跃、金融繁荣的热土上,某财险公司作为行业内的佼佼者,始终致力于通过科技创新提升业务运营效率与服务品质。随着公司业务规模的不断扩大,IT基础设施的复杂性和重要性日益凸显,如何实现对庞大IT基础资源的实时监控…