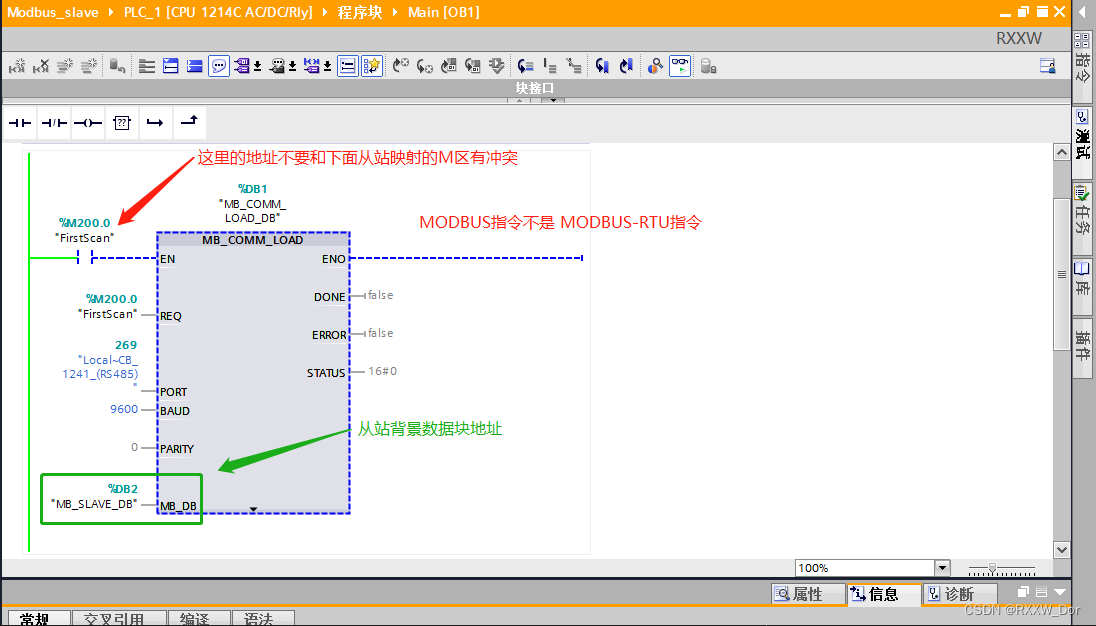
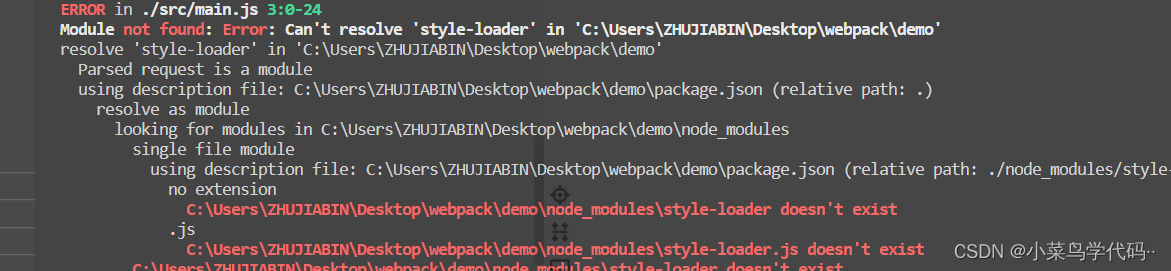
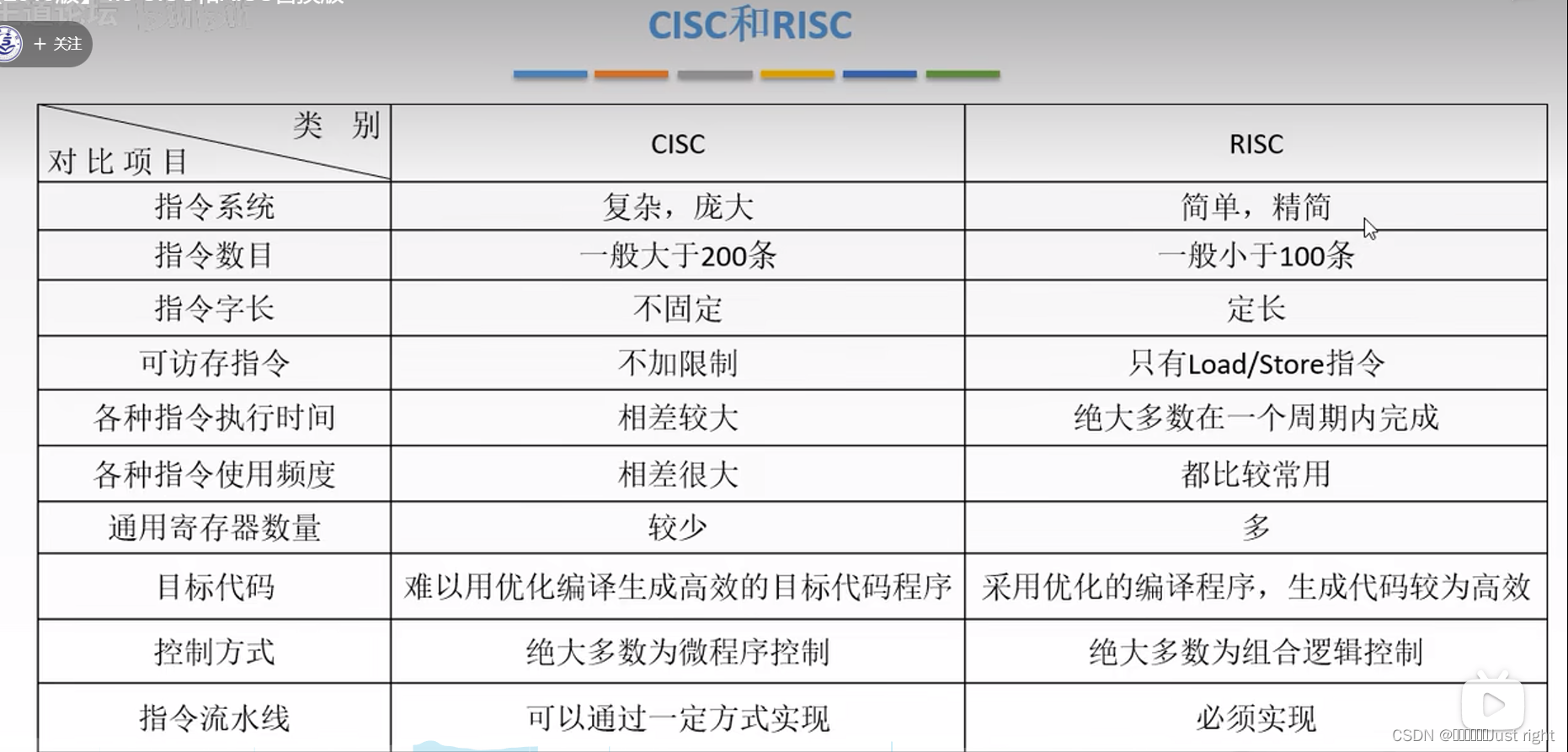
矩阵相关的计算性质
1.矩阵的某一行*一个常数
2.矩阵的一行加(减)另一行
3.交换矩阵的两行
两个未知数两个方程

线程方程组解的结构

以几何的角度查看
矩阵的方式
初等矩阵

采用初等变换的方式
在矩阵的元素中进行操作 相关的性能的变化
采用点阵的乘法,在矩阵的维度进行处理
将矩阵的内部变换,转换成矩阵的乘法

在矩阵的角度,采用相关的计算方法进行变换

采用矩阵的乘法 进行初等变换
在单位矩阵中改变相关的结果
使用矩阵的操作中,是可以在矩阵的角度,来改变矩阵的变化
矩阵的初等变化:
1.矩阵的某一行乘以某个常数
2.矩阵的一行加减另一行的若干倍数
交换矩阵的两行
初等矩阵
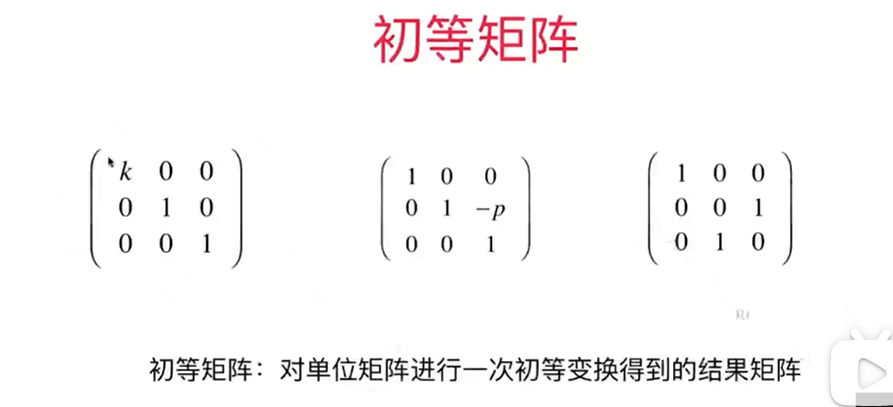
初等矩阵:
对单位矩阵进行一次初等变换得到的结果矩阵, 通常记做E
高斯消元法 --- 对矩阵进行不断单位矩阵的乘积
高斯消元法

初等矩阵和可逆性质
高斯消元法的本质是:


初等矩阵和可逆性
线性系统的角度和初等变换的角度求解矩阵的逆
矩阵的逆来解决线性系统

在得到A的可逆的情况下,可以求解线性方程组B


举证A是可以 用一些列初等矩阵表示