一、概念解析

单调栈：具有单调（递增或递减）性质和栈性质的数据结构
时间复杂度为 O(n)
单调队列：具有单调（递增或递减）性质和队列性质的数据结构
时间复杂度可以是O(1)、O(logn)、O(n)

两者的区别：
单调队列其实是单调栈的一个plus版本，或者说是具有[l, r]区间性质的单调栈（单调栈一般来说是[0, r]类型的）。
换句话说，对于单调栈能做出来的题目，基本上单调队列也能操作出来，而且请注意一点，单调队列适用范围更加广阔。
题外话，单调队列是动态规划算法一个必备的优化手段，在大公司面试题目中频频出现。

二、单调栈

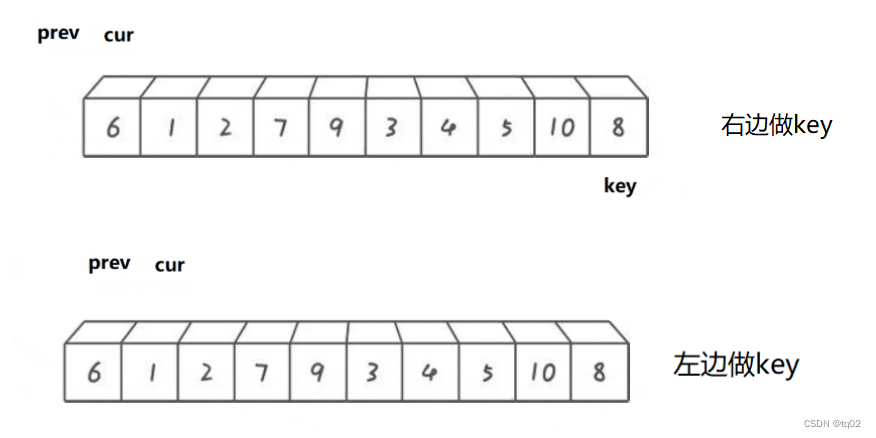
在栈顶push一个元素时，为了维护栈的单调性，需要在保证将该元素插入到栈顶后整个栈满足单调性的前提下弹出最少的元素。
为什么是最少呢？如下例子，如果是最多的话，插入元素14时，我们还可以弹出元素81，这不符合我们想要的结果。

在这里插入图片描述

int stk[N];		// 数组stk存的是元素的下标
int tt = 0;		// 栈顶
for (int i = 1; i <= n; i++) {
	while (tt && check(stk[tt], i)) tt--;	// check意为判断栈顶何时出栈，while可以不止出栈一个元素
	stk[++tt] = i;
	......									// 其他按题目要求实现
}

👉 单调栈练习题：点我跳转👈
👇练习题AC代码👇

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 10;
int h[N], v[N], stk[N], sum[N];
int n;

int main(){
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d%d", &h[i], &v[i]);
	
	int tt = 0;
	for (int i = 1; i <= n; i++) {
		while (tt && h[stk[tt]] <= h[i]) {	// 如果栈不空，并且新元素的高度比栈顶的大，将栈顶元素出栈
			sum[i] += v[stk[tt]];
			tt--;
		}
		sum[stk[tt]] += v[i];				// 因为第i个元素要入栈，根据题意加上相应能量
		stk[++tt] = i;						// 元素i入栈
	}
	
	int ans = 0;
	for (int i = 1; i <= n; i++) ans = max(ans, sum[i]);
	printf("%d", ans);
}

三、单调队列

单调队列对于任何一个数而言，只会在队列中出现一次，一旦这个数对于最后答案没有贡献了就会及时地将它删除。单调队列限制只能从队尾插入，但能从两端删除（双端队列），队列中保持单调性。对于一个数而言，新插入的数是具有潜力的并且自身价值比它还高的，那么它就出队。

int q[N];	// 数组q存的是元素的下标
int hh = 1, tt = 0;	// 队头、队尾
for (int i = 1; i <= n; i++) {
	while (hh <= tt && check_out(q[hh])) hh++;		// check_out判断队头是否超出队列长度，while可以不止出队一个元素
	while (hh <= tt && check(q[tt], i)) tt--;		// check判断队尾何时出队
	q[++tt] = i;									// 队尾重新指向下标
	......											// 其他按题目要求实现
}

check_out和check是我们需要根据题意去实现的，如下练习题可以帮助更好掌握单调队列
👉二分+单调队列练习题：点我跳转 👈
👇练习题AC代码👇

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;
int n, s, t;
int nums[N], q[N];
double sum[N];

// 对当前为i的这个位置，设前t个前缀和最小的一个位置为j
// 然后sum[i]-sum[j]便是前缀和最大的那一个
bool check(double mid)
{
	for (int i = 1; i <= n; i++)
		sum[i] = sum[i-1] + nums[i] - mid;

	int hh = 1, tt = 0;
	for (int i = s; i <= n; i++) {
		while (hh <= tt && i-q[hh] > t) hh++;
		// 单调队列维护最优值，根据题意，显然sum[a]<=sum[b]&&a>b说明第i个没什么用
		while (hh <= tt && sum[q[tt]] > sum[i-s]) tt--;
		q[++tt] = i-s;
		// 队首是最小的，前缀和最大便是sum[i]-sum[q[hh]]
		// 但是这个序列长度可能大于T，所以才有前面的i-q[hh] > t
		if (hh <= tt && sum[i]-sum[q[hh]] >= 0) return true;
	}
	return false;
}

int main(){
	cin >> n >> s >> t;
	for (int i = 1; i <= n; i++) scanf("%d", &nums[i]);
	double l = -1e4, r = 1e4;
	while (r - l > 1e-4) {
		double mid = (l + r) / 2;
		if (check(mid))  l = mid;
		else r = mid;
	}
	printf("%.3f\n", l);
}