【My Electronic Notes系列——逻辑函数的化简】

news2025/4/18 21:40:02

序言：

🏆🏆人生在世，成功并非易事，他需要破茧而出的决心，他需要永不放弃的信念，他需要水滴石穿的坚持，他需要自强不息的勇气，他需要无畏无惧的凛然。要想成功，你得付出沉重的代价。

🔥🔥 一、逻辑代数的基本定律

🔥🔥 二、逻辑函数的常用化简方法

1.并项法

2.吸收法

3.消去法

4.消项法

🔥🔥 三、最小项表达式及卡诺图

①最小项的定义

②最小项表达式

③最小项卡诺图表示法

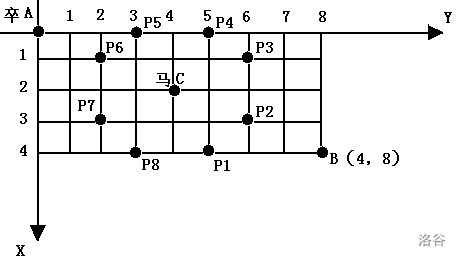
（1）存在两个变量A,B时

（2）存在三个变量A,B,C时

④卡诺图的定义

⑤用卡诺图表示逻辑代数的方法

⑥卡诺图化简法

（1）依据

（2）化简方法

两个相邻的小方格可以合并成一项，同时消去一个互反的变量（化简方法）

四个相邻的小方格构成正方形、长方形或位于四角可以合并成一项，同时消去两个互反的变量（化简方法）

八个相邻的小方格组成长方形合并成一项，同时消去三个互反变量（化简方法）

⑦卡诺图“圈1”技巧

序言：

本文章仅粉丝可见，望谅解🙏🙏

从本篇文章开始就进行电子笔记的一个汇总，属于个人的权限文章，所以设置为粉丝可见，再次望谅解🙏🙏

🏆🏆人生在世，成功并非易事，他需要破茧而出的决心，他需要永不放弃的信念，他需要水滴石穿的坚持，他需要自强不息的勇气，他需要无畏无惧的凛然。要想成功，你得付出沉重的代价。

组合逻辑电路的组成：

由基本逻辑电路和复合逻辑电路的组成。

特点：

电路没有记忆功能，输出仅取决于当时的输入状态，而与电路原来状态无关。

一、逻辑代数的基本定律

二、逻辑函数的常用化简方法

1.并项法

$AB+A\overline{B}=A$

推导： $\mathbf{{\color{Red} AB+A\overline{B}=A\left ( B+\overline{B} \right )=A\cdot 1=A}}$

2.吸收法

$A+AB=A$

推导： $\mathbf{{\color{Red} A+AB=A\cdot 1+AB=A\left ( 1+B \right )=A\cdot 1=A}}$

3.消去法

$A+\overline{A}B=A+B$

推导： $\boldsymbol{\mathbf{}{\color{Red} \textbf{}A+\overline{A}B=A+AB+\overline{A}B=A+\left ( A+\overline{A} \right )B=A+B}}$

4.消项法

$AB+\overline{A}C+BC=AB+\overline{A}C$

推导： $\mathbf{{\color{Red} AB+\overline{A}C+BC=AB+\overline{A}C+\left ( A+\overline{A} \right )\cdot BC=AB\left ( 1+C \right )\overline{A}C\left ( 1+B \right )=AB+\overline{A}C}}$

三、最小项表达式及卡诺图

①最小项的定义

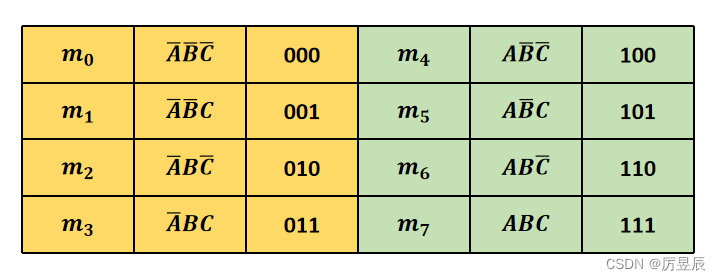
如果一个函数的某个乘积项包含了全部变量，其中，每个变量以原变量或反变量的形式出现，且仅出现一次，则这个乘积项称为该函数的一个标准积项，通常称为最小项。

最小项的表示方法：通常用符号 $m_{i}$ 来表示最小项。

3个变量A,B,C可组成8个最小项：

②最小项表达式

任何一个逻辑函数都可以表示成唯一的一组最小项之和，称为标准与或表达式。

可利用 $A+\overline{A}=1$ 和 $A\left ( B+C \right )=AB+AC$ 来配项展开成最小项表达式。

eg： $f\left ( A,B,C \right )=AB+B\overline{C}+\overline{A}B\overline{C}$

$\Rightarrow AB\left ( C+\overline{C} \right )+B\overline{C}\left ( A+\overline{A} \right )+\overline{A}B\overline{C}$

$\Rightarrow ABC+AB\overline{C}+AB\overline{C}+\overline{A}B\overline{C}+\overline{A}B\overline{C}$

$\Rightarrow ABC+AB\overline{C}+\overline{A}B\overline{C}$

$\Rightarrow m_{7}+m_{6}+m_{2}$

③最小项卡诺图表示法

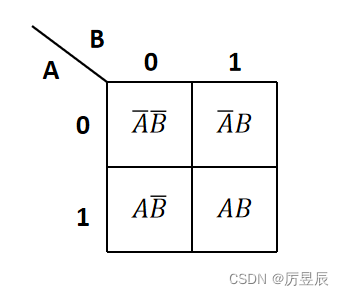
（1）存在两个变量A,B时

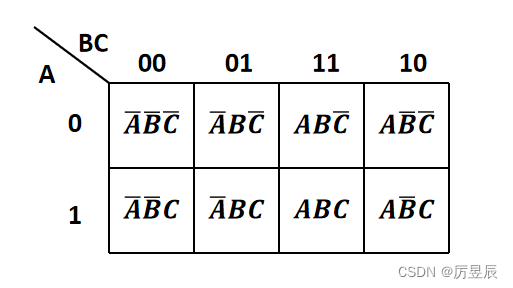
（2）存在三个变量A,B,C时

④卡诺图的定义

由许多个小方格组成的阵列图，每个小方格对应一个最小项（n个变量有 $2^{n}$ 个小方格）。

⑤用卡诺图表示逻辑代数的方法

（1）根据变量数画空白卡诺图；

（2）将逻辑代数化成最小项和的形式；

（3）在空白卡诺图上，与函数最小项对应的方格填入1，其他的填0。

eg：

$f\left ( A,B,C \right )=AB+B\overline{C}+\overline{A}B\overline{C}$

$\Rightarrow AB\left ( C+\overline{C} \right )+B\overline{C}\left ( A+\overline{A} \right )+\overline{A}B\overline{C}$

$\Rightarrow ABC+AB\overline{C}+AB\overline{C}+\overline{A}B\overline{C}+\overline{A}B\overline{C}$

$\Rightarrow ABC+AB\overline{C}+\overline{A}B\overline{C}$

又∵存在三个变量A,B,C

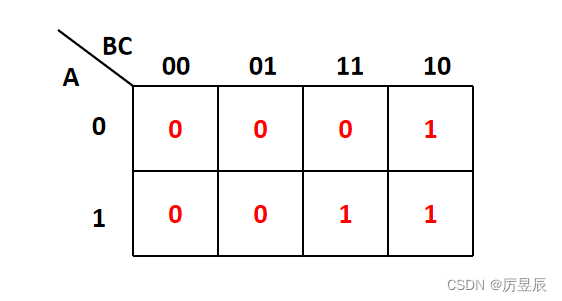
⑥卡诺图化简法

（1）依据

任何两个几何上相邻的小方格表示的最小项只有一个不同，其余变量均相同（基本特点）

利用 $AB+A\overline{B}=A$ 可以将相邻两个最小项并为一项，消去一个互反的变量。

（2）化简方法

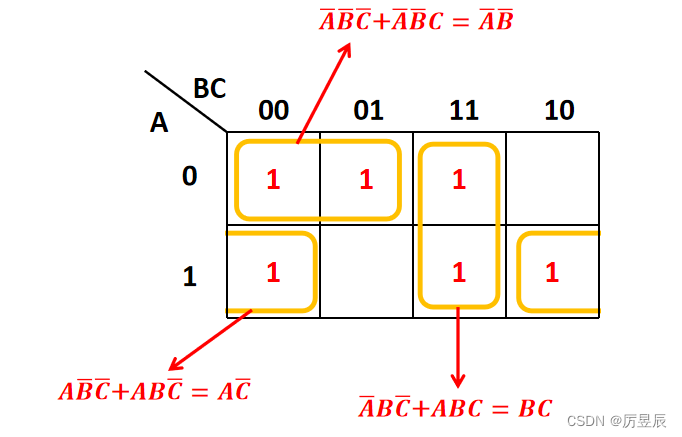
两个相邻的小方格可以合并成一项，同时消去一个互反的变量；
四个相邻的小方格构成正方形、长方形或位于四角可以合并成一项，同时消去两个互反的变量；
八个相邻的小方格组成长方形合并成一项，同时消去三个互反变量。

两个相邻的小方格可以合并成一项，同时消去一个互反的变量（化简方法）

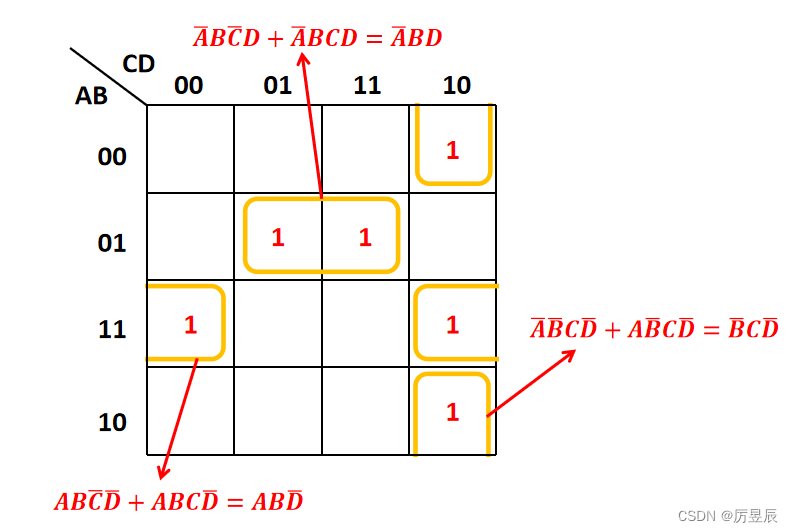
四个相邻的小方格构成正方形、长方形或位于四角可以合并成一项，同时消去两个互反的变量（化简方法）

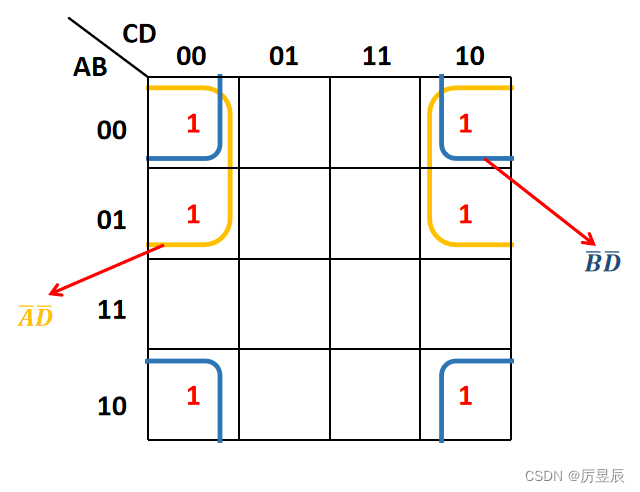
八个相邻的小方格组成长方形合并成一项，同时消去三个互反变量（化简方法）

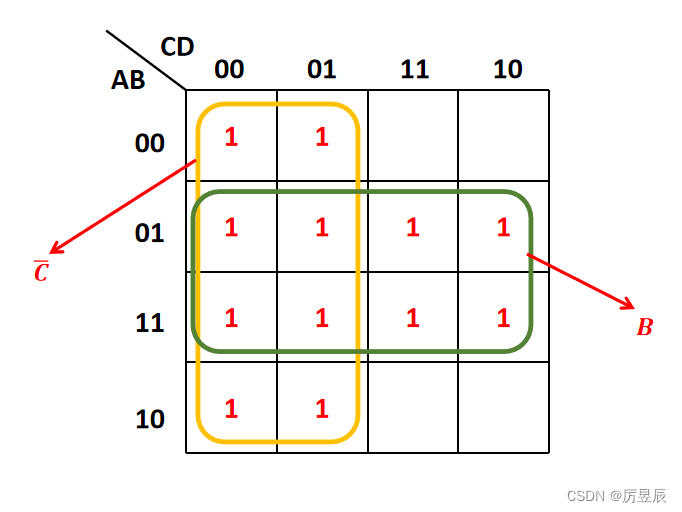
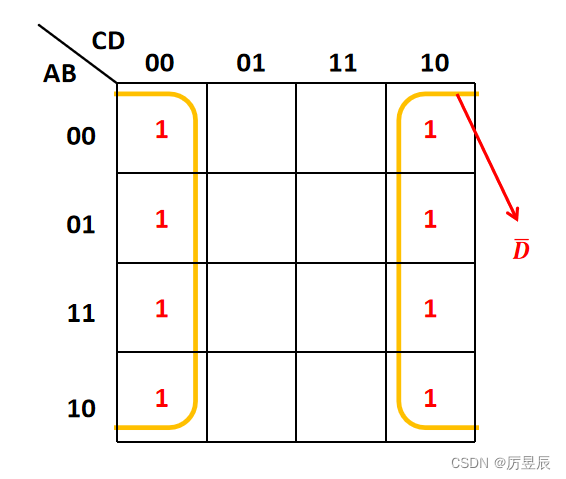
化简步骤：

①用卡诺图表示逻辑函数；

②按化简方法，将相邻的1方格圈起来，直到所有1方格被圈完为止；

③将每个圈所表示的最小项写出并相加，得到逻辑函数的最简与或表达式。

⑦卡诺图“圈1”技巧

①圈应尽量大，圈越大，消去的变量越多；

②圈的个数应尽量少，圈越小，或项越少；

③先圈孤立的1方格，再圈仅与另一个1方格唯一相邻的1方格，最后再先大圈后小圈圈定。不要遗漏任何1方格，否则函数会出错。

④同一个1方格可以被圈多次，但每个圈应包含未被圈过的1方格，否则该圈所表示的与项是多余的。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/197071.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

【My Electronic Notes系列——逻辑函数的化简】

序言：

🏆🏆人生在世，成功并非易事，他需要破茧而出的决心，他需要永不放弃的信念，他需要水滴石穿的坚持，他需要自强不息的勇气，他需要无畏无惧的凛然。要想成功，你得付出沉重的代价。

一、逻辑代数的基本定律

二、逻辑函数的常用化简方法

1.并项法

2.吸收法

3.消去法

4.消项法

三、最小项表达式及卡诺图

①最小项的定义

②最小项表达式

③最小项卡诺图表示法

（1）存在两个变量A,B时

（2）存在三个变量A,B,C时

④卡诺图的定义

⑤用卡诺图表示逻辑代数的方法

⑥卡诺图化简法

（1）依据

（2）化简方法

两个相邻的小方格可以合并成一项，同时消去一个互反的变量（化简方法）

四个相邻的小方格构成正方形、长方形或位于四角可以合并成一项，同时消去两个互反的变量（化简方法）

八个相邻的小方格组成长方形合并成一项，同时消去三个互反变量（化简方法）

⑦卡诺图“圈1”技巧

相关文章